Готовые ответы по интегрированию функций взяты из контрольной работы для студентов 1, 2 курсов математических факультетов. Чтобы формулы в задачах и ответах не повторялись условия заданий выписывать не будем. Вам и так известно, что в задачах нужно или "Найти интеграл", или "Вычислить интеграл". Поэтому если Вам нужны ответы по интегрированию то начинайте изучать следующие примеры.
Интегрирование иррациональных функций
Пример 18. Выполняем замену переменных под интегралом. Для упрощения вычислений за новую переменную выбираем не только корень, а весь знаменатель. После такой замены интеграл преобразуется к сумме двух табличных интегралов, которые и упрощать не надо
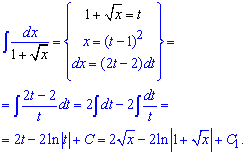
После интегрирования вместо переменной подставляем замену.
Пример 19. На интегрирования этой дробной иррациональной функции потрачено много времени и места и даже не знаем, сможете ли Вы что-то разобрать с планшета или телефона. Чтобы избавиться от иррациональности, а тут имеем дело с корнем кубическим за новую переменную выбираем корневую функцию в третьем степени. Далее находим дифференциал и заменяем предыдущую функцию под интегралом
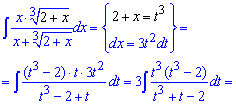
Больше всего времени занимает расписание новой функции на степенные зависимости и дроби
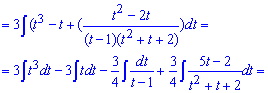
После преобразований часть интегралов находим сразу, а последний расписываем на два которые превращаем согласно табличных формул интегрирования
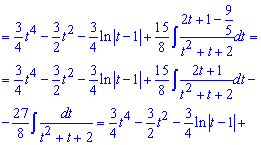
После всех вычислений не забываем вернуться к выполненной в начале замене
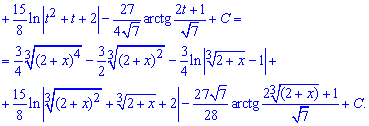
Интегрирование тригонометрических функций
Пример 20. Нужно найти интеграл от синуса в 7 степени. Согласно правилам один синус нужно загнать в дифференциал (получим дифференциал косинуса), а синус в 6 степени расписать через косинус. Таким образом придем к интегрированию от функции новой переменной t = cos (x). При этом придется подносить разницу к кубу, а потом уже интегрировать
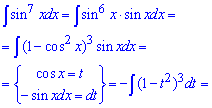
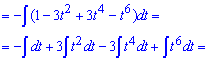
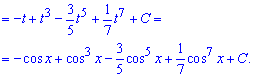
В результате получим полином 7 порядке от косинуса.
Пример 21. В этом интеграле необходимо косинус 4 степени за тригонометрическими формулами расписать через зависимость от косинуса в первой степени. Далее применяем табличную формулу интегрирования косинуса.
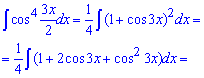
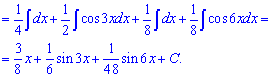
Пример 22. Под интегралом имеем произведение синуса на косинус. Согласно тригонометрическим формулам произведение расписываем через разницу синусов. Как получили эту дужку, можно понять из анализа коэффициентов при «икс». Далее интегрируем синусы
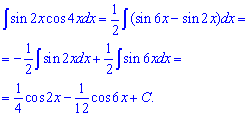
Пример 23. Здесь имеем в знаменателе одновременно и синус и косинус функцию. Причем тригонометрические формулы упростить зависимость не помогут. Для нахождения интеграла применим универсальную тригонометрическую замену t=tan(x/2)
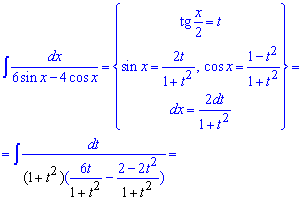
Из записи видно что знаменатели сократятся и получим в знаменателе дроби квадратный трехчлен. В нем выделяем полный квадрат и свободную часть. После интегрирования придем к логарифму от разницы простых множителей знаменателя. Для упрощения записи и числитель и знаменатель под логарифмом умножили на двойку.
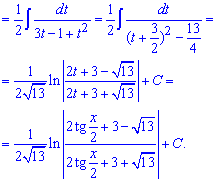
В конце вычислений вместо переменной подставляем тангенс половины аргумента.
Пример 24. Для интегрирования функции вынесем квадрат косинуса за скобки, а в скобках вычтем и добавим единицу чтобы получить котангенс.
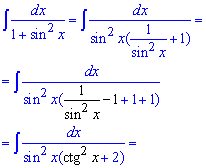
Дальше за новую переменную выбираем котангенс u = ctg (x), ее дифференциал нам даст нужный для упрощения множитель. После подстановки придем к функции которая при интегрировании дает арктангенс.
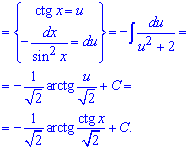
Ну и не забываем поменять u на котангенс.
Пример 25. В последнем задании контрольной работы нужно проинтегрировать котангенс двойного угла в 4 степени.
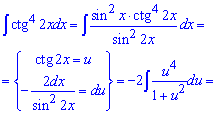
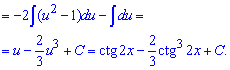
На этом контрольная работа на интегрирование решена, причем ни один преподаватель к ответам и обоснованию преобразований не придерется.
Если научитесь так интегрировать, то тесты или срезы по теме интегралы для Вас не страшны. Все остальные имеют возможность научиться или заказать решения интегралов у нас (или наших конкурентов :))).
Готовые решения контрольных с интегрирования


