Вычисление двойных и тройных интегралов

Правильно расставить пределы интегрирования в двойном и тройном интегралах не такое тяжелое задание, особенно если выполнено построение области интегрирования или имеете представление пространственного тела. Но в большинстве случаев - на практике, контрольной или экзамене студенты не имеют возможности качественно выполнить графический анализ, визуально проанализировать области, а еще большая проблема, что многие из них не владеют техникой изменения порядка интегрирования. В отдельных задачах такой подход позволяет возвести вычисление от интегрирования по 2 -3 областям к одной. В результате быстро удается найти площадь криволинейной трапеции (фигуры на плоскости) или объема тела. Для круговых, эллиптических и разных лепестковых фигур целесообразно выполнять переход к полярным координатам, а уже в них через несколько определенных интегралов найти площадь или объем. Детальный разбор готовых ответов к указанным примерам позволяет в быстрый срок выучить методику и лучше понимать теоретический материал на кратные интегралы. Все задания взяты из индивидуальной работы для студентов ЛНУ им. І. Франко, варианты хорошо подобраны и охватывают несколько тем из высшей математики.

ВАРИАНТ - 5

Вычисление двойных интегралов

ЗАДАНИЕ 1.23 Поменять порядок интегрирования в двойном интеграле:
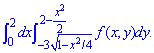Решение: Методика вычислений к подобным задачам заключается в следующем:
сначала выписываем область интегрирования из интеграла, которая ограничена кривыми

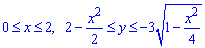
Дальше превращаем функции, чтобы найти их канонический вид.
Верхний предел y=2-x²/2 - парабола с вершиной в точке O(0;2) и ветками вниз.
Возводим к каноническому виду нижний предел интегрирования

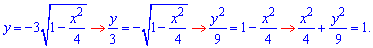
Получили полуелипс с центром в точке S (0;0) и полуосями a=2, b=3.
Изобразим кривые в декартовой системе координат (СК)
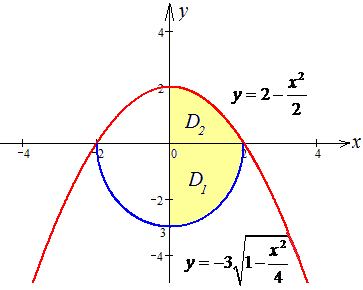Выражаем полученные функции через переменную y:
Из первой 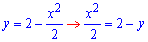получим корневую зависимость 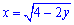, перед радикалом стоит знак "+" поскольку часть параболы находится в правой (положительной по x) части плоскости;
Для эллипса будем иметь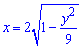
При изменении порядка интегрирования область нужно разбить на две части: D=D₁+D₂.
Расставим пределы интегрирования в каждой половине:

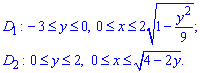
Изменяем пределы в двойном интеграле

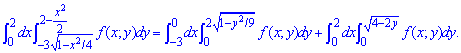
ЗАДАНИЕ 2.24 Найти площадь плоской фигуры, заданной следующими условиями: y=x²-4x+3, y=x+1, y=-2x+5.
Решение: Задание достаточно творческое, ведь искомая фигура имеет следующий график. Но это забегая наперед
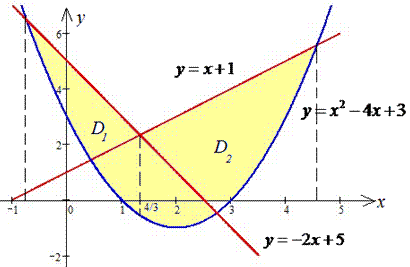На практике Вы этого не знаете, потому начинаете анализ с поиска точек пересечения графиков заданных функций:
Сначала 1 и 2

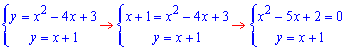
отсюда

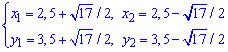
Дальше 2 и 3

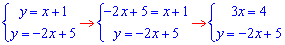
отсюда

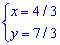
И напоследок 1 и 3

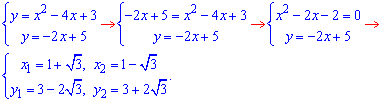
Координаты точек пересечения содержат корень, ето значит что преподаватель, который готовил задание особенно не старался, чтобы облегчить работу студентам и получить напоследок хороший ответ.
Заданную область можно разбивать на 2-4 части, все зависит от порядка интегрирования.
Мы же заданную область будем разбивать на две области:
D=D₁+D₂, как на рисунке.
Расставим пределы в каждой области:

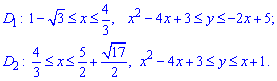
С помощью двойного интегралу вычислим площадь фигуры, ограниченной параболой и линиями, :

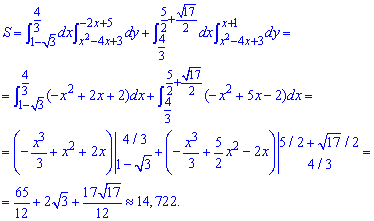
Интегрировать не трудно, однако комментировать пределы во второй раз не будем.

ЗАДАНИЕ 3.25 Вычислить двойной интеграл по области D, ограниченной указанными линиями: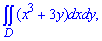
, D: x+y=1, y=x²- 1 .

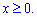Решение: Найдем точки пересечения графиков заданных функций : y=1 - x и y=x²- 1:
1 - x=x²-1, x²+x-2=0, (x-1)(x+2)=0, x=1, y=0.
Изобразим область интегрирования в декартовой СК
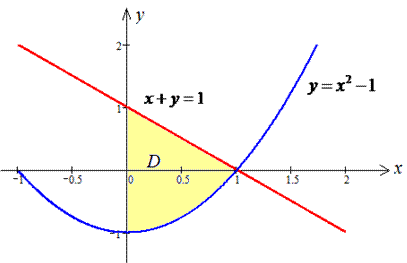Расставим пределы интегрирования при переходе от параболы к прямой:

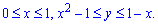
Вычислим двойной интеграл заданной функции :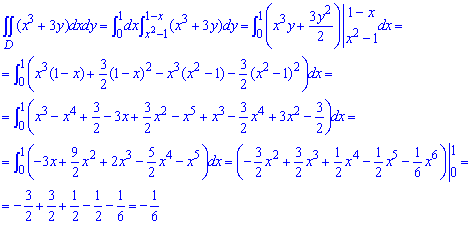
.
Получили отрицательный интеграл I=-1/6.

ЗАДАНИЕ 4.6 Вычислить двойной интеграл, используя полярные координаты: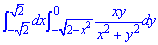

Решение: Сведем функции пределов интегрирования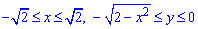 к каноническому виду

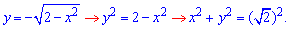
Получили круг с центром в точке O (0;0) и радиусом корень из двух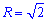 (нижняя половина).
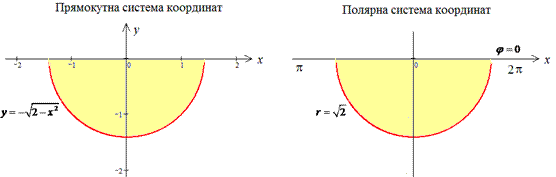Для перехода к полярной системе координат применяем замену переменных :

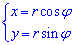
При этом подинтегральную функцию следует умножить на якобиан перехода:
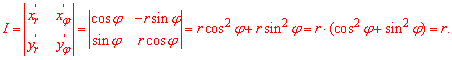Превратим подинтегральную функцию под полярные координаты:

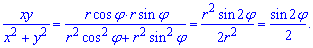
Запишем пределы интегрирования в полярной системе координат :

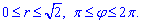
Вычислим двойной интеграл в полярной СК:
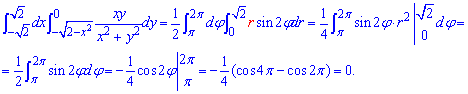Он равен 0, это значит, что подинтегральная функция непарная в заданной области. Это легко видеть из ее начальной записи.

ЗАДАНИЕ 5.7 Вычислить площадь области D, ограниченной указанными линиями:
D: y²=4x, x²=4y.

Решение: За инструкцией находим точку пересечения двух графиков
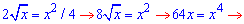x₁=0, y₁=0; x₂=4; y₂=4.
Расставим пределы интегрирования в заданной области D:

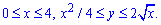
Построим график фигуры за известными уравнение функций
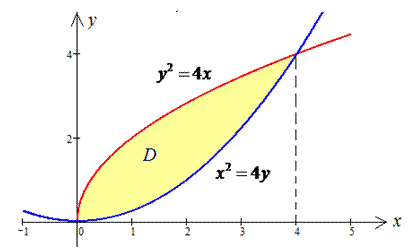Площадь фигуры находим за формулой:
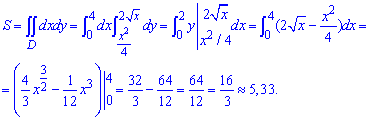Внутренний интеграл предусматривает подстановку пределов интегрирования и только во внешнем придется использовать формулы интегрирования.
Площадь фигуры ровна S=16/3 единиц квадратных.

ЗАДАНИЕ 6.8 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры :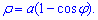

Решение: Уравнение rho=a (1 - cos (phi)) описывает кардиоиду в полярной системе координат.
График кардиоиды имеет вид
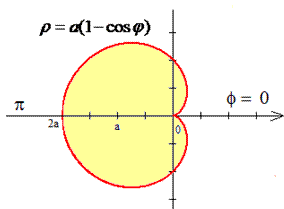Поскольку заданная функция парная, то вычислим половину площади и результат умножим на 2.
Записываем пределы интегрирования для верхней половины фигуры :

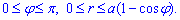
Через двойной интеграл находим площадь кардиоиды :
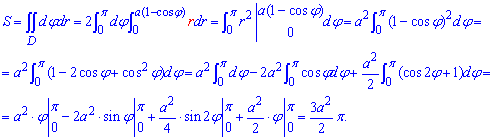Под интегралом пришлось использовать формулы понижения степени для квадрату косинуса.
Также, обратите внимание, что во всех примерах при нахождении интегралов в полярных координатах функция под интегралом должна содержать множителем якобиан перехода.

 Вычисление тройных интегралов

ЗАДАНИЕ 7.9 Найти объем тела, заданного поверхностями, что его ограничивают:
x²/9+y²/4+z²=1, x²+y²=2x, z=0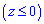

Решение: Первая поверхность x²/9+y²/4+z²=1 - эллипсоид с полуосями a=3, b=2, c=1.
Вторую сведем к каноническому виду x²+y²=2x, (x-1)²+y²=1² - коловий цилиндр вытянут вдоль оси Oz.
Запишем функции заданных поверхностей в той плоскости, где будем искать объем тела :

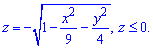
Построим трехмерную модель тела и его проекцию в декартовую плоскость

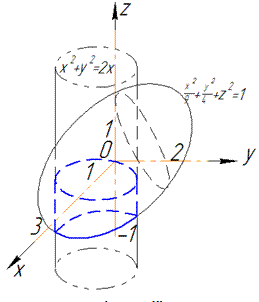
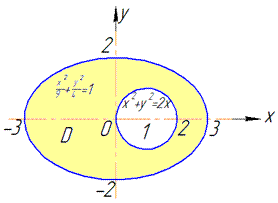
Объем тела, которое ограничено заданными поверхностями, найдем как разницу объемов полэллипсоида и полуцылидндра, который ограничен снизу плоскостью z=-1. При расстановке пределов интегрирования будем учитывать четность заданных функций и результат умножим на 2.
Сначала найдем объем тела, которое ограничено півеліпсоїдом.
Расставим пределы интегрирования в заданной области:

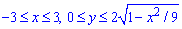
 через двойной интеграл найдем объем полэллипсоида
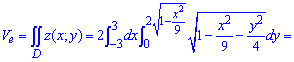согласно рекомендаций, для упрощения вычислений перейдем к полярной системе координат (запишем формулы перехода и якобиан)
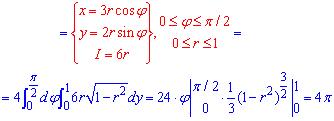Найдем объем полцилиндра, который ограничен плоскостью z=-1.
Поверхность ограничена следующими пределами:

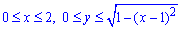
Подставляем их в формулу объема тела и рассчитываем
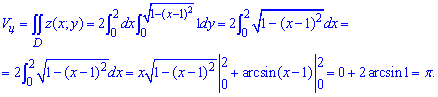Конечный объем вычисляем как разницу между полуелипсом и полуцылиндром :

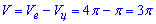
он равен V=3pi кубических единиц.

ЗАДАНИЕ 8.10 Расставить пределы интегрирования в тройном интеграле 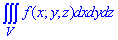, если область V ограничена указанными поверхностями:

V: x=2, y=4x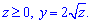
Нарисовать область интегрирования.
Решение: Уравнение поверхности в пространстве запишем из последнего условия: z=y²/4 - это параболический цилиндр.
Пересечение поверхностей в пространстве и проекция тела в декартовую плоскость изображено на рисунку ниже
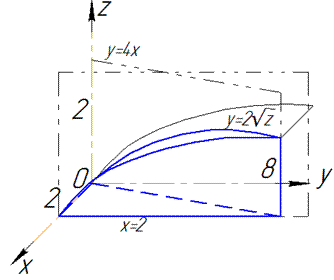
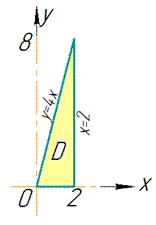Пределы интегрирования расставим следующим образом:
V: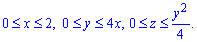
Записываем тройной интеграл с учетом найденных пределов

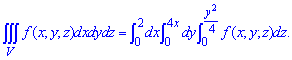
ЗАДАНИЕ 9.11 Вычислить тройные интегралы: 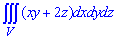, где V: .

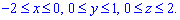Решение: Выполняем построение поверхностей интегрирования

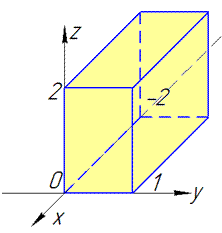
Заданная область V является параллелепипедом, кроме этого подинтегральная функция задана в явном виде xy+2z.
Подставляем пределы в тройной интеграл и находим его значение

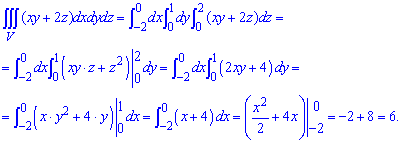
Формулы интегрирования для примера не тяжелые и его по силам найти всем.

ЗАДАНИЕ 10.12 Используя тройной интеграл, вычислить объем тела : где y=2x, y=3,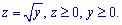
Нарисовать область интегрирования.

Решение: Сначала выполняем построение вспомогательного рисунка. Проекция тела на плоскость дает прямоугольный треугольник

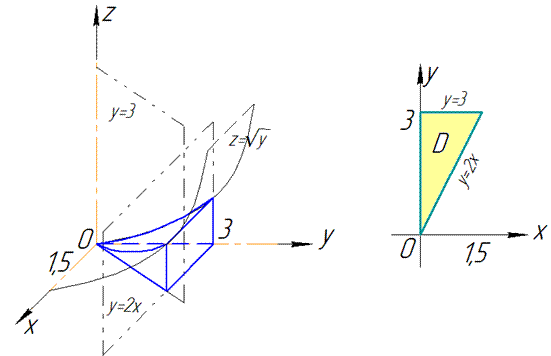
Запишем пределы интегрирования, учитывая условие и выполненный рисунок :

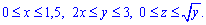
Подставим пределы в тройной интеграл и найдем объем тела :

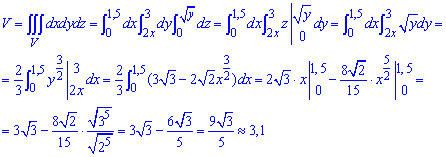
Само интегрирование расписано в деталях, потому проанализируйте расчеты из формулы.
На этом контрольная из высшей математики решена, выводы относительно эффективности тех или других приемов каждый должен сделать самостоятельно.
В дополнение можем лишь сказать, что Вы всегда можете обратиться к нам за консультацией относительно вычислений двойных и тройных интегралов.