Готовые интегралы функций приведены из контрольной работы для студентов 1, 2 курсов математических факультетов. Решения помогут изучить не только схемы интегрирования, но и познакомят с разнообразными приемами вычисления, облегчат вычитание интегралов. Некоторые задания сложные и их могут встретить в обучении лишь часть математиков, экономистов, статистов, физиков.
Интегрирование дробных функций
Пример 15. Следующие примеры на схему интегрирование дробей методом разложения. Сначала знаменатель расписываем на простые множители, далее в зависимости от их вида дробную функцию записываем через простые дроби с неизвестными постоянными.
![]()
![]()
Правую сторону сводим к общему знаменателю
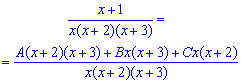
и раскрыв скобки группируем слагаемые при одинаковых степенях «икс».
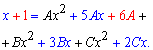
Приравняв коэффициенты при одинаковых показателях переменной приходим к системе линейных уравнений (СЛАУ) с которой находим постоянные. Систему можно вычислять методом Крамера, Гаусса, можете хоть пользоваться "Эксель" или МатКад. Главное найти константы
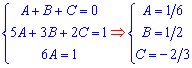
Далее значение подставляем в разложение дробной функции и интегрируем
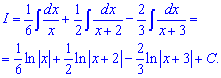
Пример 16. Задано интеграл дробной рациональной функции. Сначала разложим знаменатель на простые множители
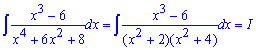
Далее записываем под интеграл функцию через сумму простых дробей с неизвестными множителями
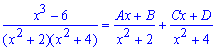
Сводим правую сторону под общий знаменатель
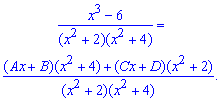
и из условия равенства числителей
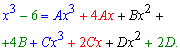
составляем систему линейных уравнений для определения 4 неизвестных постоянных.
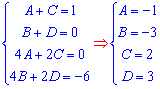
После вычисления СЛАУ возвращаемся к разложению и выполняем интегрирования дробей
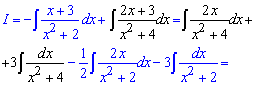
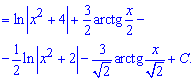
Пример 17. Еще одна задача на интегрирование дробной функции. По приведенной выше схеме вычислений расписываем знаменатель
![]()
и записываем простые дроби для отыскания 3 постоянных.
![]()
После возведения под общий знаменатель из коэффициентов при одинаковых степенях переменной
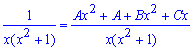
составляем систему уравнений. На этот раз она достаточно проста и коэффициенты разложения находим из формул
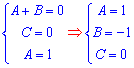
Далее подставляем множители в дроби и проводим интегрирование
![]()
В результате вычислений получим два логарифма от модулей функций. Во втором слагаемом модуль можно не ставить, поскольку подмодульная функция везде положительная.
Остальные готовые ответы по контрольной работе на интегралы Вы найдете в следующих публикациях. Задания на интегралы и схемы их вычислений помогут разобраться с большинством простых интегралов.
Готовые решения контрольных с интегрирования


