ЗНО з математики. Тригонометрія

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.

Розділ 1. Числа

В завданнях 1.37 - 1.68 правильна відповідь оцінюється 2 балами.

Завдання 1.59 (Т-07, 39) Обчисліть 2*sin(15)*соs(15)*tg(30°)*ctg(30°).
Розв'язання: Маємо завдання на знання формул тригонометрії. Добуток синуса на косинус рівний половині синуса подвійного кута. Також відомо, що тангенс помножений на котангенс завжди рівний одиниці. Звідси обчислення виразу можна записати формулами
2*sin*(15)*соs(15)*tg(30)*ctg(30)=2*sin(30)*1=2*(1/2)*1=1.
Як бачите, розрахунки доволі прості, тож подібні завдання Ви на тестах розв'язати зобов'язані.
Відповідь: 1.

Завдання 1.60 Спростіть вираз (tg (а) + сtg (а))*sіn 2а.
Розв'язання: З вигляду незрозуміло, що з таким записом робити. Проте на практиці все доволі просто – розписуємо тангенс і котангенс через синус і косинус кута, та зводимо під спільний знаменник.

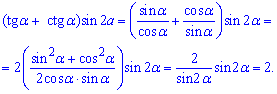
В результаті неважких маніпуляцій отримали двійку.
Відповідь: 2.

Завдання 1.61 (Т-06, 5) Обчисліть значення виразу sin(2а) , якщо ctg(a)=-1/2. Відповідь запишіть десятковим дробом.
Розв'язання: Синус подвійного кута через тангенс виражається універсальною тригонометричною підстановкою

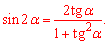
Оскільки нам задано котангенс, то тангенс визначаємо із формули
tg(a)*ctg(a)=1;
tg(a)=1/ctg(a)=1/(-1/2)=-2.
Підставляємо у формулу синуса подвійного кута та спрощуємо

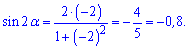
Запам'ятати дану формулу досить важко, проте без неї подібних обчислень виконати не вдасться.
Відповідь: -0,8.