Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.
Розділ III. Функції
В завданнях 3.46 - 3.62 правильна відповідь оцінюється 2 балами.
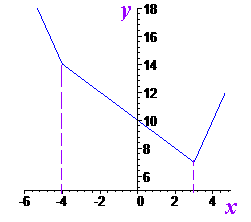
Завдання 3.51 Знайдіть найменше значення функції f(х)=2|х-3|+|х+4|.
Розв'язання: Маємо суму модуль функцій. Вона має мінімуми в точках де підмодульні функції перетворюються в нуль.
В даному випадку це x=3; x=-4. Знаходимо мінімуми функції
f(3)=2*0+7=7;
f(-4)=2*7=14.
В трійці значення менше, отже мінімум модуль функції рівний 7. Графік функції у вигляді ламаної прямої має вигляд
В нулях модулів маємо злами, а сам графік багато чого відкриває нового для тих, хто має невелику практичну базу аналізу модуль функцій.
Відповідь: 7.
Завдання 3.52 Знайдіть, при яких значеннях параметра а дотична до графіка функції у=х3+ах2 у точці з абсцисою х0=-1 проходить через точку N(3;4).
Розв'язання: Складемо рівняння дотичної до графіка функції. Для цього обчислимо похідну функції
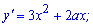
та підставимо точку
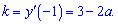
Сама ж функція в точці дотику рівна
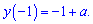
Підставляємо отримані значення в рівняння дотичної
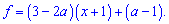
Далі з умови, що дотична проходить ще через одну точку знаходимо параметр
f(3)=4;
(3-2a)(3+1)+a-1=4;
12-8*a+a-1=4;
-7*a=4-11=-7;
a=1.
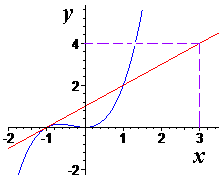
Як бачите завдання не складне, головне знати – що шукати? І як шукати. І як бонус наведемо Вам сам графік заданої функції та дотичної до неї
З побудови бачимо, наскільки легко можна застосовувати похідну, а саме знання дотичної до графіків функцій.
Відповідь: 1.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Аналіз функції за графіком
- Наступна стаття - ЗНО 2017 математика. Найбільше значення функції на проміжку