ЗНО математика. Рівняння підвищеної складності

Шановні школярі, випускники, абітурієнти, цей розділ допоможе при підготовці до зовнішнього оцінювання 2017 року з математики. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці до тестування, систематизувати та підвищити накопичений рівень знань з математики.

Розділ II. Рівняння і нерівності

Розв'язання завдань 11.87 - 11.94 повинне мати обґрунтування. Запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання завдань схемами, графіками, таблицями.

Завдання 11.87 Розв'яжіть нерівність

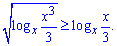
Розв'язання: Задана логарифмічна нерівність, причому непроста, оскільки в основі стоїть змінна. А це значить, що нерівність потрібно буде розв'язувати на двох інтервалах (0;1) та (1; безмежність). Піднесемо нерівність до квадрату, щоб позбутися кореня з першого логарифма

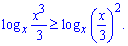
Далі розкриваємо нерівність і обидві частини множимо на 9, щоб не мати справи з дробами

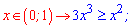
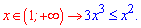
Розв'язуємо кожну з нерівностей на інтервалі

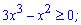
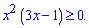
Нулями нерівності є значення x=0; x =1/3.
Підстановкою точки з інтервалу переконуємося, що розв'язком буде інтервал

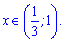
Розглянемо другу нерівність

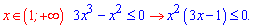
Нулі ті ж самі, тільки знак нерівності потрібен протилежний. На даному інтервалі нерівність не виконується, отже відповіддю буде знайдений раніше інтервал.
Відповідь: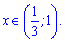

Завдання 11.88 Задано нерівність

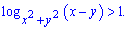
а) Побудуйте у прямокутній декартовій системі координат множину допустимих значень змінних х та у .
б) Побудуйте у прямокутній декартовій системі координат множину точок (х; у), координати яких задовольняють задану нерівність та знайдіть площу цієї фігури.
Розв'язання: Завдання досить цікаве і повчальне. Таким прикладом можна перевірити знання множин, логарифмічних рівнянь, геометрії. В основі маємо квадратне рівняння. Не рівність треба розбивати на дві.
a) Перша коли основа менша одиниці, тобто внутрішня частина круга одиничного радіуса
x²+y²<1.
Функція під логарифмом повинна бути додатною
x-y>0;
y <x. Другий випадок коли маємо зовнішність кола x2+y2> <x.
Звідси область визначення матиме вигляд

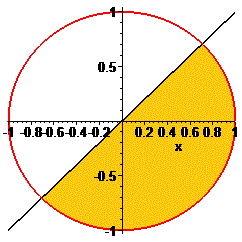
Для зовнішності круга рівняння залишиться тим самим. Тобто областю визначення буде все, що знаходиться справа від круга і прямої

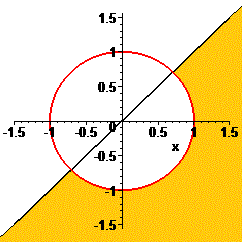
Остаточно множина допустимих значень відповідає сектору, що знаходиться нижче лінії y=x за виключенням кола одиничного радіуса. Графічно це можна уявити, як об'єднання наведених графіків.

б) Знайдемо розв'язок нерівності на області визначення. Спершу розкриємо нерівність на внутрішній частині круга

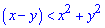
Перетворимо нерівність до повного квадрату

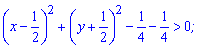
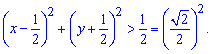
Розв'язком нерівності є внутрішня частина круга одиничного радіусу без круга заданого рівнянням, що знайшли. Графік множини розв'язків наведено графічно

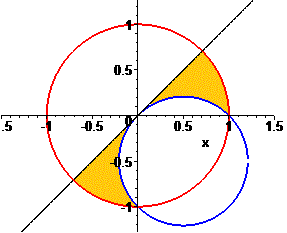
Розкриємо нерівність при основі більшій одиниці

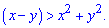
Перетворимо рівняння виділивши повний квадрат

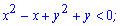
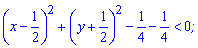
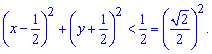
Отже розв'язком буде множина перетину області визначення, тобто зовнішньої частини круга одиничного радіуса з внутрішньою частиною круга з центром в (1/2; -1/2) і радіусом корінь з 2 розділити на 2. Графічно при основі більший одиниці множина розв'язків матиме вигляд

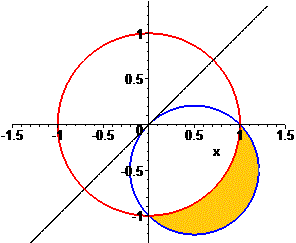
Кінцева множина розв'язків логарифмічної нерівності є об'єднанням знайдених і графічно має вигляд

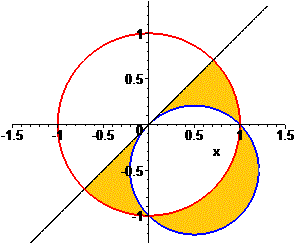
Як знайти площу заштрихованої частини перетину кіл ми Вам наводити не будемо. Дивує, як такі завдання може розв'язати школяр після закінчення школи?

Завдання 11.89 Знайдіть всі значення параметра а, при яких всі розв'язки нерівності ах² - х +1 - а < 0 задовольняють нерівність 0< х <1
Розв'язання: Підемо класичним шляхом, розв'яжемо квадратне рівняння, яке задане і знайдемо і інтервали, які задовольняють нерівність. Обчислюємо дискримінант рівняння
D=1-4a(1-a) =1-4a+4a²=(1-2a)²
Корені рівняння

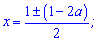
x=-a;
x=-1+a. a>0;
-1+a=1; a=1+1=2

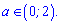
Відповідь:

Завдання 11.90 Задано рівняння sin х + соs х = a/sinx.
а) Розв'яжіть рівняння при а = 0.
б) Розв'яжіть рівняння при всіх значеннях параметра а.
Розв'язання: При параметрі рівному нулю тригонометричне рівняння матиме вигляд
sin(х) + соs(х) = 0.
Розв'язок легко знайти на колі одиничного радіуса, а потім описати формулами.
Графік кутів, які задовільняють рівняння має вигляд

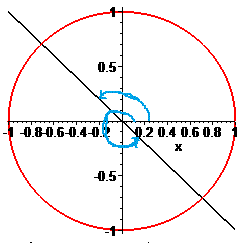
Далі записуємо градусну міру наведених кутів

Варіант б розглядати не будемо. Хто має якісь міркування як знайти відповідь, просьба надіслати нам на пошту. ЗНО з математики з таким підходом до перевірки знань школярів може більше нашкодити статистичній інформації про освіту, ніж показати реальний рівень знань випускників.

Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.

Відповіді до ЗНО тестів