Наведені відповіді ЗНО з математики шукає велика кількість учасників майбутнього тестування. Вони достатньо складні проте ідеї для їх вирішення простіші і будуть Вам корисними. Також можете розв'язувати самостійно подібні завдання із збірників, спеціально написаних для підготовки до ЗНО.
Завдання 28. Знайдіть найменший додатний період функції
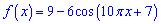
Розв'язання: Період визначається за формулою.
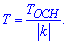
Для синус і косинус функцій основний період становить 2*Пі.
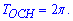
Коефіцієнт k відповідає множнику при х 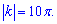 Обчислюємо період
Обчислюємо період
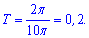
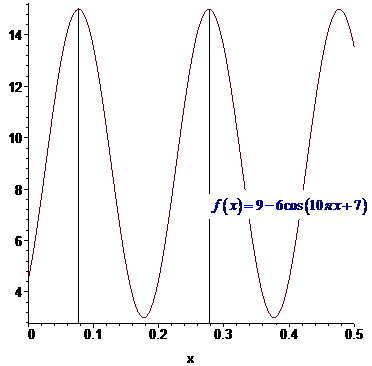
Для наочності, графік функції наведено нижче.
Відповідь: 0,2.
------------------------------
Завдання 29. В автобусному парку налічується n автобусів, шосту частину яких було обладнано інформаційними табло. Пізніше інформаційні табло встановило ще на 5 автобусів з наявних у парку. Після проведеного переобладнання навмання вибирають один з n автобусів парку. Ймовірність того, що це буде автобус з інформаційним табло становить 0,25. Визначте n . Уважайте, що кожен будинок обладнується лише одним табло.
Розв'язання: За класичним означенням ймовірність рівна
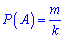
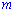 – число сприятливих умов
– число сприятливих умов
,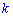 – число всіх умов події
– число всіх умов події 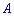 .
.
Число обладнаних автобусів становило 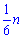 , а після встановлення
, а після встановлення
ще п'яти стало
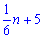
звідки
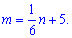
Із умови, що ймовірність вибрати обладнаний автобус рівна 0,25 або 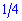 знаходимо кількість автобусів
знаходимо кількість автобусів
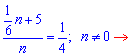
Позбуваємося знаменників
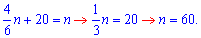
Відповідь: 60.
------------------------------
Завдання 30. План паркової зони, обмеженої трикутником АВС, зображено на малюнку. Дуга АВ – велосипедна доріжка. Відомо що дуга АВ є четвертою частиною кола радіуса 1,6 км. СА і СВ – дотичні до цього кола (А і В – точки дотику). Обчисліть площу зображеної на плані паркової зони (у 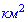 ).
).
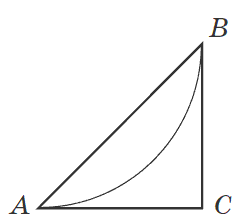
Розв'язання: Площу трикутника обчислюємо за формулою
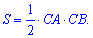
Оскільки CA і CB є дотичними до кола, за малюнком, то вони рівні радіусу CA=CB=1,6 км. На основі цього знаходимо площу паркової зони
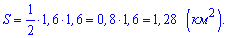
Відповідь: 1,28.
------------------------------
Завдання 31. На рисунку зображено графік функції
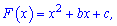
яка є первісною для функції 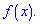 Визначте параметри b і c, знайдіть функцію
Визначте параметри b і c, знайдіть функцію 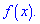 У відповіді запишіть значення
У відповіді запишіть значення 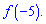
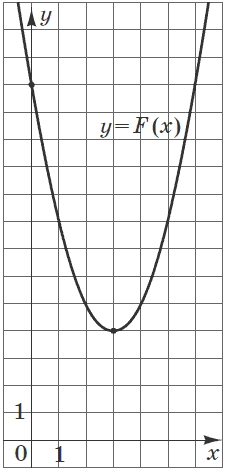
Розв'язання: З малюнку невідома частина графіку, в якій знаходиться шукана точка, однак бачимо, що це парабола загальне рівняння якої має вигляд
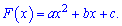
Графік первісної 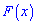 перетинає вісь ординат в точці (0;13), звідки знаходимо F(0)=с=13. Вершина параболи розташована в точці з координатами (3;4), Абсцису вершини знаходимо за формулою
перетинає вісь ординат в точці (0;13), звідки знаходимо F(0)=с=13. Вершина параболи розташована в точці з координатами (3;4), Абсцису вершини знаходимо за формулою
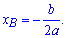
З графіку бачимо, що a=1 – парабола розташована вітками вгору, якщо вниз то мали б a=-1. Абсциса точки В рівна 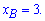 Знаходимо значення
Знаходимо значення
b 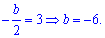
Рівняння параболи матиме вигляд
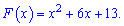
Для відшукання 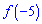 знаходимо похідну від первісної
знаходимо похідну від первісної
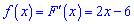
Та підставляємо точку
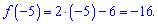
Відповідь: - 16.
------------------------------
Завдання 32. Основою піраміди S ABCD є трапеції ABCD  , довжина середньої лінії якої дорівнює 5 см. Бічне ребро SB перпендикулярне до площини основи піраміди і вдвічі більше від середньої лінії трапеції ABCD. Знайдіть відстань від середини ребра SD до площини SBC (у см), якщо об'єм піраміди дорівнює
, довжина середньої лінії якої дорівнює 5 см. Бічне ребро SB перпендикулярне до площини основи піраміди і вдвічі більше від середньої лінії трапеції ABCD. Знайдіть відстань від середини ребра SD до площини SBC (у см), якщо об'єм піраміди дорівнює 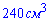 .
.
Розв'язання: Завдання достатньо складне і мало хто із школярів за нього брався. Наведемо графічну побудову піраміди.
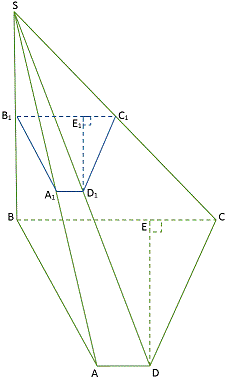
ABCD – за умовою трапеція, площу якої знаходимо за формулою
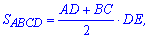
в якій відома
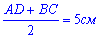
середня лінія,  – висота трапеції ABCD. Отже площа основи піраміди рівна
– висота трапеції ABCD. Отже площа основи піраміди рівна 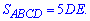 Об'єм піраміди визначається за формулою
Об'єм піраміди визначається за формулою
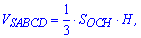
тут 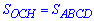 – площа основи,
– площа основи, 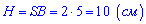 – висота піраміди.
– висота піраміди.
Підставимо в формулу об'єму
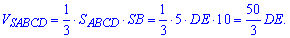
Оскільки об'єм піраміди відомий і становить 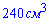 , то
, то  буде рівним
буде рівним
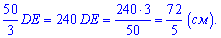
очка 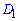 – середина ребра
– середина ребра 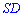 . Для обчислення віддалі від точки
. Для обчислення віддалі від точки 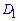 до площини
до площини 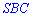 , проводимо через точку
, проводимо через точку 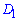 перетин піраміди, паралельний до її основи. Перетином буде подібна основі трапеція
перетин піраміди, паралельний до її основи. Перетином буде подібна основі трапеція 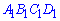 . За властивостями пропорцій знаходимо
. За властивостями пропорцій знаходимо
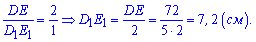
Відповідь: 7,2.
------------------------------
Завдання 33. Знайдіть значення параметра а, при якому корінь рівняння
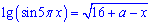
належить проміжку 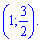
Розв'язання: Розпочнемо аналіз із встановлення ОДЗ:
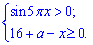
Оскільки коренева функція додатно визначена, то ліва частина теж додатня
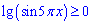
або

Проте синус функція обмежена
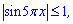
отже
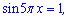
і відповідно ліва
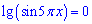
та права частина
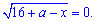
приймають нульові значення. Розв'язуємо перше рівняння.
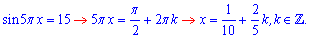
За умовою аргумент належить інтервалу 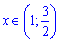 . Звідси отримаємо
. Звідси отримаємо
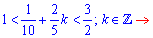
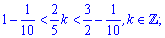
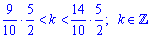
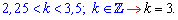
При цьому
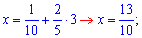
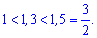
Розв'язуємо праву частину
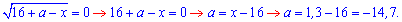
та знаходимо значення параметру.
Відповідь: -14,7.
-----------------------------------
Переглянути розв'язки завдань № 22-27 ЗНО-2013 математика


