Сьогодні навчимося використовувати формулу Байєса для обчислення ймовірності гіпотез. Але спершу трохи теорії.
Нехай маємо повну групу гіпотез-подій H1..Hn, які попарно несумісні. Подія А якщо може відбутись, то тільки з однією з перелічених гіпотез.
Тому події A рівна сумі попарно несумісних подій A•Hi, а її ймоврність за теоремою додавання рівна
P(A)=P(A•H1)+...+P(A•Hn)=P(H1)•P(A/H1)+...+P(H1)•P(A/Hn),
де P(A/Hi) – умовні ймовірності події A при гіпотезі Hi.
Остання права частина і є формулою повної ймовірності.
Виникає питання, як знайти ймовірність гіпотез коли подія А відбулася P(Hi/A).
Оскільки справедливі зворотні рівності
P(Hi•A)=P(A)•P(Hi/A)=P(Hi)•P(A/Hi)
то з них виводять формулу ймовірності гіпотези коли подія А відбулася
P(Hi/A)=P(Hi)•P(A/Hi)/P(A).
Ймовірність гіпотез ще називають формулою Байєса.
В інтернеті ви можете зустріти ймовірність гіпотези в дещо інших позначеннях
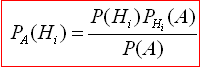
Наведемо готові задачі з теорії ймовірності на формулу Байєса.
Приклад 1. У магазині реалізується продукція двох фірм, і частка кожної, відповідно рівна:
1-ї фірми – 60%, 2-ї фірми – 40%.
Для продукції кожної з фірм брак, відповідно, становить:
1-а фірма – 3%,
2-а фірма – 5%.
Яка ймовірність того, що навмання придбана в магазині одиниця продукції є доброякісна (подія А)?
Якщо це так, то яка ймовірність, що доброякісна продукція належить першій фірмі?
Розв'язання: Тут можливі дві події-гіпотези:
H1 − продукція вироблена на першій фірмі,
H2 − продукція з 2 фірми.
Вони утворюють повну групу подій, а їх ймовірності відповідно рівні:
P(H1) =60%/100% =0,6;
P(H2) =40%/100%=0,4.
Позначимо подія А − навмання придбана одиниця продукції доброякісна.
Відповідні умовні ймовірності події А становлять:
P(A/H1) =1−3%/100% =0,97;
P(A/H2) =1-5%/100%=0,95.
Тут ймовірності шукали як різницю повної ймовірності і протилежної події (придбана навмання одиниця продукції є бракована).
Далі, за формулою повної ймовірності знаходимо P(A):
P(A)=p(H1)•p(A/H1)+p(H2)•p(A/H2)=0,6•0,97+0,4•0,95=0,582+0,38=0,962.
Щоб знайти ймовірність, що при цьому доброякісна продукція вироблена 1 фірмою застосуємо формулу Байєса
P(A/H2)=p(H1)•p(A/H1)/P(A)=0,582/0,962≈0,605.
Відповідь: 0,962; 0,605.
Приклад 2. За даними страхової компанії, ймовірність того, що водій потрапить в аварію протягом року, дорівнює 0,05. Проте якщо відомо, що стаж водіння менший від 2 років, то така ймовірність становить уже 0,15. Серед водіїв 25 % мають стаж менше від 2 років. Знайдіть ймовірність того, що у водія, який потрапив в аваpію протягом року, стаж водіння був меншим від 2 років.
Розв'язування: Позначимо через H1, H2 гіпотези, що водій має стаж водіння та ні відповідно.
Тоді ймовірності гіпотез дорівнюють
p(H1)=25%/100%=0,25;
p(H2)=1-0,25= 0,75.
Нехай подія А полягає в тому, що водій потрапив в аварію.
Тоді умовні ймовірності становлять
p(A/H1)=0,15;
P(A/H2)=0,05.
За формулою повної ймовірності знаходимо P(A):
P(A)=p(H1)•p(A/H1)+p(H2)•P(A/H2)=0,25•0,15+0,75•0,05=0,075.
Для обчислення ймовірності, що уводія що потрапив в аварію стаж був меншим за два роки застосуємо формулу Байєса:
P(H1/A)=p(H1)•p(A/H1)/P(A)=0,25•0,15/0,075=0,5.
Відповідь: 0,5.
Приклад 3. У першій урні міститься 4 білих і 3 чорних кульки, а в другій – 3 білих і одна чорна кулька. З першої урни навмання вийняли 1 кульку і переклали її в другу. Знайти ймовірність того, що після перекладання навмання вийнята з другої урни кулька буде білою.
Розв'язання: Завдання потрібно розв'язувати через повну ймовірність.
Позначимо через B1 гіпотезу, що в другу урну з першої переклали білу кульку, через B2 – переклали чорну кульку.
Тоді ймовірність гіпотез рівна
p(B1)=4/7,
p(B2)=3/7.
В другій урні стане 4 білих і всього n=3+1+1=5 кульок при B1, і 3 білих з 5 при гіпотезі B2. Тоді умовні ймовірності рівні пропорціям білих кульок в другій урні
p(A/B1)=4/5;
p(A/B2)=3/5.
Шукану ймовірність витягнута білу кульку з другої урни знаходимо за формулою повної ймовірності
P=P(B1)•P(A/B1)+p(B2)•P(A/B2)=
= 4/7•4/5+3/7•3/5=25/35=5/7=0,7143.
Відповідь: 0,7143.
Приклад 4. Пасажир може звернутися за квитком в одну з трьох кас. Ймовірності звернення в кожну з кас залежать від їх місцезнаходження співвідносяться як 2:3:5. Ймовірності і наявності квитків у цих касах відповідно дорівнюють 0,8; 0,1; 0,2.
Знайти ймовірність того, що пасажир придбав квиток в одній з кас? В якій з кас найімовірніше був куплений цей квиток?
Розв'язання: Позначимо за H1,H2,H3- гіпотези, що пасажир звернувся за квитком в 1,2, 3 касах відповідно.
Тоді ймовірності гіпотез із співвідношення 2:3:5 рівна:
p(H1)=2/(2+3+5)=0,2 p(H2)=3/10=0,3 p(H3)=5/10=0,5.
Подія А полягає в тому, що пасажир купив квиток.
Ймовірності купити квиток в кожній з кас рівні
p(A/H1)=0,8 p(A/H2)=0,1 p(A/H3)=0,2.
За формулою повної ймовірності знаходимо p(A):
p(A)=p(H1)•p(A/H1)+p(H2)•p(A/H2)+p(H3)•p(A/H3)=
= 0,2•0,8+0,3•0,1+0,5•0,2=0,16+0,03+0,1=0,29.
Ймовірність складається з суми трьох доданків, і кожен з них є вкладом кожної з кас в купівлю квитка.
Оскільки перший доданок, що входить в тільки що розраховану ймовірність, найбільший то найімовірніше квиток куплений в першій касі.
Щоб в цьому переконатися, застосуємо формулу Байєса
p(H1/A)=p(H1)•p(A/H1)/p(A)=0,16/0,29≈0,55.
Відповідь: 0,29; в першій касі.
Приклад 5. У першому ящику маємо 8 і 2 дефектні деталі, а у другому – 5 стандартних і 5 дефектних.
З навмання вибраного ящика взято дві деталі. Яка ймовірність того, що вони є стандартними?
Яка ймовірність, що ця деталь взята з другого ящика?
Розв'язання: Позначимо через B1, B2, що деталі взяті з першого або другого ящика відповідно. Оскільки в них по 10 деталей, то ймовірність події однакова і рівна
p(B1)=0,5 p(B2)=0,5.
Позначимо А – взято 2 стандартні деталі.
Ймовірність, що з першого ящика взято 2 стандартні деталі з 2 рівна
p(A/B1)=8/10•7/9=0,62(2).
Оскільки спершу маємо 8 стандартних з 10, після того як 1 вибрали – залишилося (8-1)=7 з (10-1)=9, тому ймовірність вибрати другою стандартну деталь =7/9.
Повірте, що багатьом з Вас таке детальне розписання дає більше ніж голі формули.
Ймовірність вибрати з 2 ящика 2 стандартні деталі з 5 при наявних 10 рівна
p(A/B2)=5/10•4/9=0,22(2).
За формулою повної ймовірності знаходимо імовірність вибрати 2 стандартні деталі
p(A)=p(B1)•p(A/B1)+p(B2)•p(A/B2)=0,5•(0,62(2)+0,22(2))=0,42(2).
Ймовірність гіпотези - деталь, що виявилася стандартною взята із другого ящика знайдемо за формулою Байєса
p(B2/A)=p(B2)•p(A/B2)/p(A)=0,50,22(2)/0,42(2)≈0,263.
Можете переконатися, що в чисельнику маємо другий доданок з ймовірності p(A), в знаменнику її саму. Тому думаю Вам зрозумілий фізичний зміст ймовірності гіпотез.
Відповідь: 0,42(2); 0,263.
Задачі для самопідготовки на формулу Байєса
Задача 1. Деталі, які виготовляє завод, можуть бути перевірені на брак одним із двох контролерів. Імовірність того, що деталь буде перевірена першим контролером – 0,7, другим – 0,3. Імовірність того, що деталь буде визнана стандартною першим контролером – 0,9, другим – 0,96. Після перевірки деталь визнана стандартною (подія А). Знайти ймовірність того, що деталь перевірив перший контролер.
Задача 2. Два мисливці незалежно один від одного стріляли по мішені, роблячи по одному пострілу. Ймовірність влучного пострілу для першого мисливця дорівнює 0,8; для другого – 0,6. Після стрільби в мішені виявлено одну пробоїну. Яка ймовірність того, що вона належить:
а) 1-му мисливцю; б) 2-му мисливцю?
Задача 3*. В лотереї в якості призу можна отримати телефон iPhone або Sumung.
Є два контейнери з телефонами, в одному 7 айфонів з 10 телефонів, в другому 9 самсунгів і 11 айфонів. Два переможці по черзі вибирають собі приз з одного контейнера. Яка ймовірність того, що обидва вибрали самсунг? Знайти ймовірність, що вибрані телефони лежали з першому контейнері.
Задача 4*. В першій урні 1 біла і 4 чорні кулі, в другій – 2 білі і 3 чорні кулі, в третій – 3 білі і 2 чорні кулі. З кожної урни вийняли по одній кулі. Знайти
ймовірність того, що серед них буде 1 біла і 2 чорні кулі.
На сайті розв'язано 100-ні задач з теорії ймовірності та інших предметів. Якщо ви прийшли до нас ще з курсу ЗНО підготовки, то думаю не один раз використовували сайт для поглиблення знань з математичних дисциплін. Просимо ділитися посиланням на сайт з друзями та надсилати нам завдання, які не можете розв'язати. Разом нам під силу освоїти все!


