Метод Гауса розв'язування систем лінійних алгебраїчних рівнянь полягає у послідовному виключенні невідомих за допомогою елементарних перетворень і зведенні до верхньої трикутної (східчастої або трапецеподібної). Після чого розв'язують систему з кінця до початку, підстановкою знайдених розв'язків.
Розглянемо приклади розв'язування систем лінійних рівнянь , взявши за довідник збірник задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Розв'язати систему лінійних алгебраїчних рівнянь.
(1. 189) 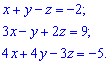
Розв'язок. Перетворимо вихідну систему до східчастого вигляду. Для цього від другого рівняння віднімемо перше. Помножена на 3, а від четвертого віднімемо перше, помножене на 4
. 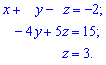
В результаті з третього рівнняня маємо z=3. Отримане значення підставляємо в попереднє рівняння для знаходження y
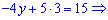 >
>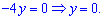
Отримані значення y,z підставляємо в перше рівняння
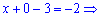
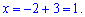
Розв'язком системи трьох лінійних рівнянь будуть наступні значення змінних
x=1; y=0; z=3.
Приклад 2. Знайти розв'язки системи лінійних рівнянь третього порядку.
(4. 195) 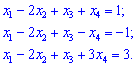
Розв'язок.Задано систему трьох рівнянь з чотирма невідомими. В таких випадках одна змінна може бути вільна, а решта будуть виражатися через неї. Зведемо систему до східчастого вигляду. Для цього від другого і третього рівняння віднімемо перше
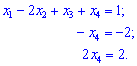
З останніх двох рівнянь отримуємо ідентичні розв'язки x4=1.
Після підстановки в перше рівняння отримаємо
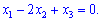
Дане рівняння зв'язує три змінних. Таким чином будь-яка зі змінних може бути виражена через дві інших
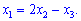
Отже отримаємо наступний розв'язок
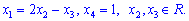
Один з коренів приймає довільне значення, інші виражаюьться через нього.
Приклад 3. Обчисити корені системи лінійних рівнянь 5 порядку.
(4. 198) 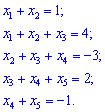
Розв'язок. Ррозріджену систему лінійних рівнянь п'ятого порядку з п'ятьма невідомими зводимо до східчастого вигляду. Від другого рівняння віднімаємо перше і записуємо у зручному для аналізу вигляді (змінні під змінними)
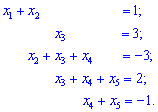
З другого рівняння знаходимо, що x3=3.
Підставляємо значення у всі нижчі рівнняння та переносимо за знак рівності. Також поміняємо друге з третім рівняння місцями
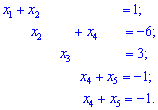
Четверте та п'яте рівняння еквівалентні. Виразимо одну зі змінних через іншу
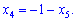
Отримане значення підставимо в друге рівняння і знайдемо x2
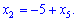
З першого рівняння визначаємо x1
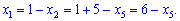
Розв'язок системи рівнянь наступний
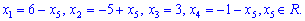
При обчисленнях систем лінійних алгебраїчних рівнянь методом Гауса потрібно звеcти систему лінійних рівннянь до східчастого вигляду. Для цього зручно записувати змінні під змінними, як в останньому прикладі, це пришвидшить розв'язування. Решта все залежить від матриці, яку потрібно розв'язати і Ваших вмінь.


