Ряд позначають так:
Вираз для n- го члена ряду при довільному натуральному n>0 , називається загальним членом ряду і позначається un.
Загальний член ряду можна задати формулою un=f(n), з допомогою якої записується довільний член ряду.
Суму n перших його членів позначають через Sn:
Sn=u1+u2+u3+...+un.
і прийнято називати n-ою частинною сумою ряду.
Часткові суми ряду утворюють деяку числову послідовність його часткових сум Sn. Ряд називається збіжним, якщо збігається послідовність його часткових сум Sn, тобто якщо існує скінчена границя
![]()
Число S при цьому називають сумою ряду і записують
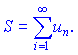
При цьому вважають також, що ряд збігається до числа S.
Якщо послідовність часткових сум ряду розбігається, то ряд називається розбіжним. У цьому випадку ряд не має суми.
Ряд, що складений з елементів геометричної прогресії називається геометричним рядом:
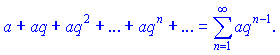
Число q — знаменник геометричної прогресії.
Позначимо Sn сума n перших членів прогресії та знайдемо її значення:
![]()
![]()
Звідси отримуємо формулу частової суми ряду
![]()
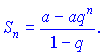
Якщо |q|<1, то суму ряду знаходимо за формулою
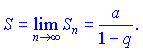
а геометричний ряд збігається.
Якщо |q|>1, то сума ряду прямує до безмежності при великих номерах
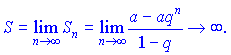
Якщо q=1, то сума теж розбіжна (прямує до безмежності)
![]()
Якщо q=-1, то маємо формулу суми, що залежить від номера
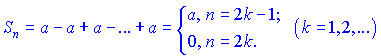
таким чином, послідовність часткових сум Sn - розбіжна.
Ряд вигляду
![]()
називається гармонічним рядом. Він розбіжний.
Числовий ряд вигляду
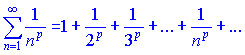
називається узагальненим гармонічним рядом. Доведено, що при p<=1 узагальнений гармонічний ряд розбігається, а при p>1 -ряд збігається.
Якщо ряд збігається, то різниця між сумою S і частинною сумою його Sn
![]()
називається n -им залишком ряду.
Залишок Rn ряду являє собою ту похибку, яка одержиться, якщо замість наближеного значення суми ряду S взяти суму перших n членів цього ряду. Але оскільки S є границя суми Sn, то для збіжного ряду виконується умова, що границя залишку прямує до нуля при номері прямуючому до безмежності
![]()
Таким чином, взявши достатньо велике число членів збіжного ряду, можна суму цього ряду обчислити з любою точністю. Звідси випливає, що основною задачею теорії рядів є дослідження збіжності ряду.
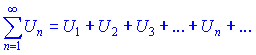 називається додатним, якщо всі його члени невід'ємні
називається додатним, якщо всі його члени невід'ємні Для того, щоб визначити чи ряд збіжний чи розбіжний в літературі зібрані правила, які дозволяють це швидко. Розглянемо по черзі ознаки збіжності числових рядів.
Ознака порівняння
Розглянемо два ряди з додатними членами
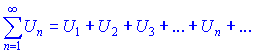
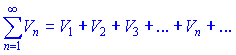
Для них виконуються наступні твердження:
1. Якщо члени ряду Un не більші відповідних членів Vn збіжного ряду ![]() (
(![]() ), то ряд Un =
), то ряд Un =![]() збігається.
збігається.
Якщо кожний член ряду ![]() більший (або рівний) відповідного члена розбіжного ряду
більший (або рівний) відповідного члена розбіжного ряду ![]() , то цей ряд
, то цей ряд ![]() розбігається.
розбігається.
Дослідження збіжності ряду
Приклад 1. Дослідити на збіжність ряди
1) 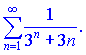
Розв'язок. Порівняємо заданий ряд
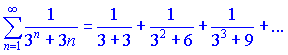
з рядом геометричної прогресії, знаменник якої рівний q=1/3
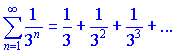
Кожен член першого ряду менший за відповідний член ряду геометричної прогресії, який збігається, оскільки q=1/3<1
![]()
За ознакою порівняння перший ряд збіжний.
2) 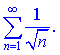
Розв'язок. Члени даного ряду порівнюємо з відповідними гармонічного ряду. Для довільного n>1 виконується нерівність
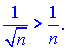
Так як гармонічний ряд розбіжний, то відповідно до ознаки порівняння заданий ряд також розбіжний. Ознака порівняння - це найпростіша з ознак, які дозволяють швидко встановити збіжність ряду.
Гранична ознака порівняння
Нехай ряди Un=![]() та Vn=
та Vn=![]() додатні, а також існує скінчена границя їх частки limit=k
додатні, а також існує скінчена границя їх частки limit=k
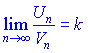
причому k відмінне від нуля число ![]() , тоді обидва ряди або одночасно збіжні, або одночасно розбіжні.
, тоді обидва ряди або одночасно збіжні, або одночасно розбіжні.
Приклад 2. Дослідити на збіжність ряд
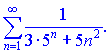
Розв'язок. Для порівняння виберемо ряд ![]() збіжної геометричної прогресії. Застосовуючи граничну ознаку, обчислюємо границю
збіжної геометричної прогресії. Застосовуючи граничну ознаку, обчислюємо границю
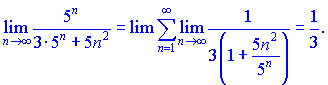
Оскільки обидва ряди ведуть себе рівносильно k=1/3, а геометричний ряд збіжний, то і розглянутий ряд також збіжний.
Ознака Даламбера
Нехай члени ряду Un
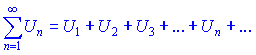
додатні і відношення n+1-го члену до попереднього n-го має скінченну границю при номері прямуючому до безмежності ![]()
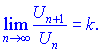
В залежності від значення границі (k) робимо висновки про збіжність чи розбіжність ряду
- Якщо k<1, то ряд збігається.
- Якщо k>1 - ряд розбігається.
- При k=1треба застосовувати іншу ознаку збіжності, оскільки дана ознака не може визначити чи збіжний ряд чи розбіжний.
Приклад 3. Дослідити на збіжність ряди
1) 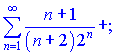
Розв'язок. Знайдемо границю n+1 члена ряду до n-го при ![]()
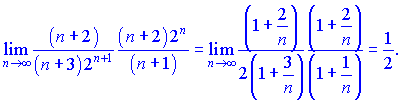
Оскільки границя k=1/2<1, то ряд збіжний.
2) 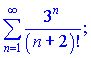
Розв'язок.Обчислимо границю частки загального члена ряду до попереднього
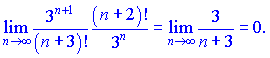
Ряд збіжний, так як границя менша одиниці k=0<1.
3) 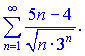
Розв'язок. Застосуємо ознаку Даламбера
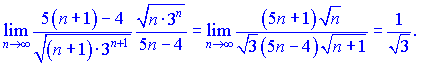
Бачимо, що ряд збіжний, оскільки границя менша за одиницю![]()
Радикальна ознака Коші
Якщо для ряду Un=![]() з додатними членами існує границя кореня n-го порядку limit=k
з додатними членами існує границя кореня n-го порядку limit=k
![]()
то при k<1 ряд збіжний, а при k>1 - розбіжний.
При k=1 потрібно застосовувати іншу ознаку збіжності.
Приклад 4. Дослідити на збіжність ряди
1) 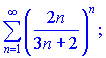
Розв'язок. Застосуємо радикальну ознаку Коші та обчислюємо границю
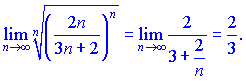
Ряд збіжний, оскільки отримали k=2/3<1.
2) 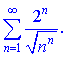
Розв'язок. Обчислимо границю кореня з загального члена ряду
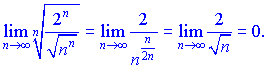
Вона рівна нулю, отже робимо висновок про збіжність ряду.
Інтегральна ознака Коші
Нехай задано ряд
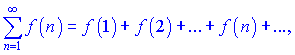
причому f(x) додатна, неперервна і монотонно спадна функція від ![]() .
.
Тоді ряд
(1) 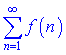 збіжний, якщо невластивий інтеграл
збіжний, якщо невластивий інтеграл
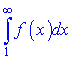 збіжний (приймає скінченне значення);
збіжний (приймає скінченне значення);
(2) ряд розбіжний, коли інтеграл розбіжний. Під збіжністю інтегралу слід розуміти його обмеженість, тобто
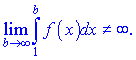
Розглянемо приклади застосування інтегральної ознаки Коші.
Приклад 5. Дослідити на збіжність
1) 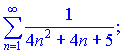
Розв'язок. Застосуємо інтегральну ознаку Коші (знаходимо інтеграл)
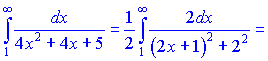
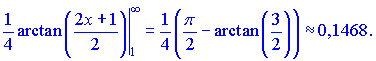
Ряд збіжний, оскільки інтеграл збіжний (=0,1468).
2) 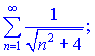
Розв'язок. Знайдемо означений інтеграл від загального члена ряду
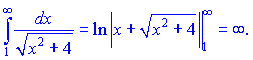
Він рівний безмежності, а це значить, що за інтегральною ознакою Коші ряд розбіжний.
3) 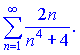
Розв'язок. Обчислимо інтеграл, для цього виконаємо заміну змінних в підінтегральній функції. В результаті отримаємо арктангенс половини аргументу, який у межах інтегрування приймає скінченне значення
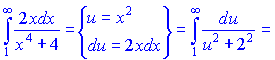
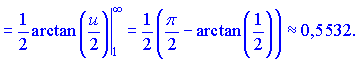
Даний ряд збіжний, оскільки Integral=0,5532.
Виористовуйте наведені ознаки збіжності рядів, аналізуйте самостійно ряди і з часом Ви почнете їх розрізняти інтуітивно.
Приклад 1. Дослідити числовий ряд на збіжність.
а) 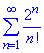
Досліджувати збіжність ряду будемо за ознакою Даламбера:
якщо границя відношення наступного члена прогресії до заданого менша одиниці і додатна 0<α<1 при номері прямуючому до безмежності 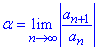 , тоді ряд
, тоді ряд 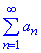 збігається, і розбігається, якщо α>1 .
збігається, і розбігається, якщо α>1 .
Виконаємо обчислення
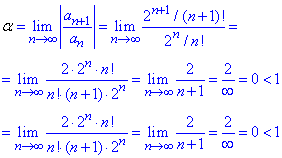
звідси слідує, що ряд 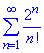 збігається.
збігається.
б) 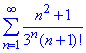
Дослідимо збіжність ряду за ознакою Даламбера:
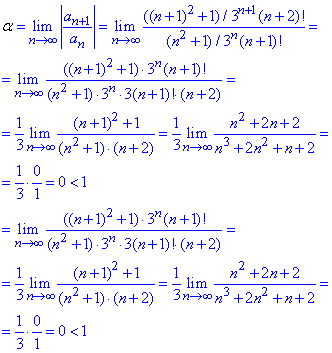
звідси слідує, що ряд 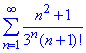 збігається.
збігається.
Приклад: 2.5 Дослідити збіжність рядів
а) 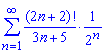
Обчислення: Оскільки даний ряд має додатні члени, то досліджувати його на збіжність будемо за допомогою ознаки Даламбера:
![]()
Записуємо загальний член ряду та наступний, що йде після нього
![]()
![]()
Та знаходимо границю їх частки
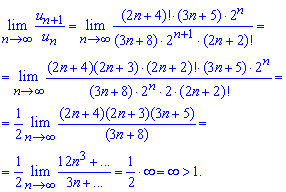
Оскільки границя нескінченна 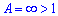 , то за ознакою Деламбера ряд розбіжний.
, то за ознакою Деламбера ряд розбіжний.
б) 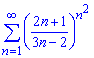
Обчислення: Члени ряду додатні, тому досліджувати на збіжність будемо за ознакою Даламбера: Записуємо формули послідовних членів ряду
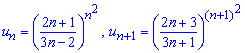
Та знаходимо границю наступного члена до попереднього при n прямуючому до безмежності
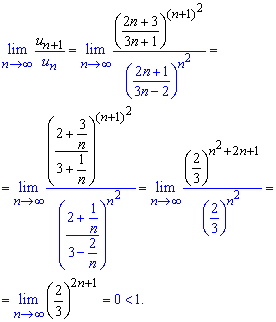
Границя рівна нулю, так як показник прямує до нескінченності, а в дужках маємо значення менше за одиницю.
За теоремою Даламбера A=0<1 ряд збігається!
Приклад: 2.8 Дослідити ряди на збіжність:
а) 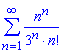
Обчислення: Як Ви вже переконалися усі приклади, що тут розглядаються слід перевіряти за ознакою Даламбера.
В результаті спрощення прийдемо до другої чудової границі – експоненти
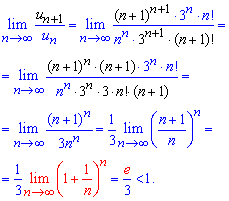
Загалом границя менша одиниці ![]() отже ряд збігається.
отже ряд збігається.
б) 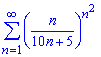
Обчислення: Для перевірки на збіжність ряду за ознакою Даламбера обчислюємо границю
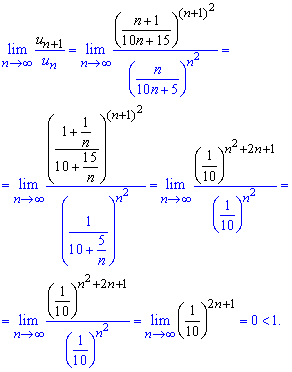
Границя рівна 0 (A=0<1), отже ряд збігається!
Приклад: 2.14 Дослідити ряд на збіжність
а) 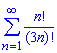
Обчислення: Знаходимо границю частки наступного члена ряду до попереднього
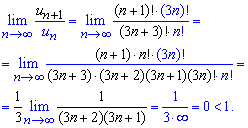
Для зручності читання формул наступний член ряду виділений під границею чорним кольором. Добре розберіться як ділити факторіал на факторіал.
За ознакою Даламбера ряд збігається!
б) 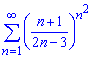
Обчислення: Записуємо формулу загального члена ряду та наступного за ним
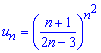
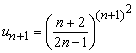
Підставляємо їх в формулу Даламбера та обчислюємо границю
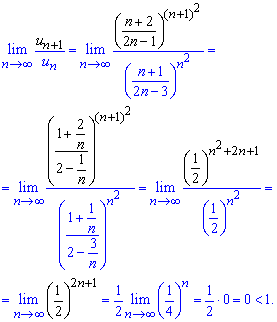
Границя рівна нулю 0<1, а це значить що даний ряд збігається.
Приклад: 2.16 Дослідити ряд на збіжність:
а) 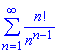
Обчислення: За ознакою Даламбера перевіряємо границю членів ряду на обмеженість
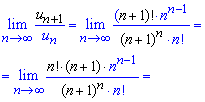
Перетворивши множники в чисельнику і знаменнику дробу зведемо функцію в дужках до другої чудової границі
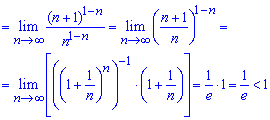
Оскільки границя менша одиниці
![]() ,
,
то за теоремою Даламбера ряд збігається.
б) 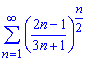
Обчислення: Задано числовий степеневий ряд з додатніми членами. Знайдемо границю відношення наступного члена ряду до попереднього
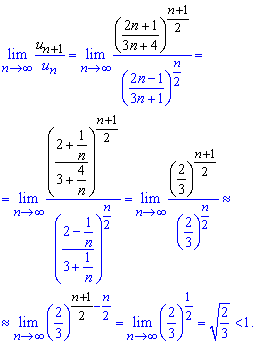
При обчисленні границі думаю всі моменти Вам зрозумілі, якщо ні то Вам потрібно переглнути категорію "границі функцій".
Отримали гранию менше одиниці,
![]()
отже за ознакою Даламбера ряд збіжний.
Приклад: 2.26 Дослідити збіжність ряду:
а) 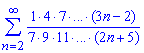
Обчислення: Для застосування ознаки Даламбера випишемо загальний член ряду та наступний за ним
![]()
![]()
Далі підставимо їх та знайдемо границю
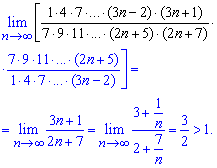
Границя рівна A=3/2>1, а це означає що даний ряд розбігається!
б) 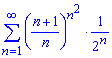
Обчислення: Записуємо два послідовні члени додатного ряду
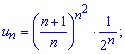
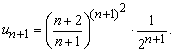
Знаходимо границю для оцінки збіжності ряду за теоремою Даламбера.
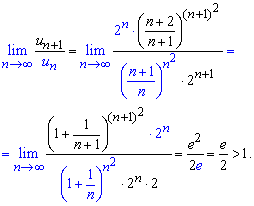
В ході обчислень отримаємо другу чудову границю (експоненту) як в чисельнику, так і в знаменнику. Результуюча границя більша одиниці ![]() , отже робимо висновок про розбіжність ряду.
, отже робимо висновок про розбіжність ряду.
Готові розв'язки на ряди:
]]>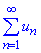 з додатними членами un>0 існує границя
з додатними членами un>0 існує границя 
Тоді: при A<1 ряд збігається;
при A>1 ряд розбігається;
при A=1 питання про збіжність ряду ознака не вирішує.
Це маєте запам'ятати, оскільки на значення границі Коші базуються висновки про збіжність або розбіжність числового ряду.
А тепер перейдемо то аналізу готових відповідей з розрахункових та екзаменаційних робіт.
Приклад 1. Дослідити на збіжність ряд
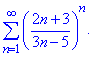
Розв'язування: Маємо додатний ряд, причому він має вигляд функції від n в степені функції від n. Це важливо, тому що тільки в такому випадку радикальна ознака Коші швидко встановлює збіжність або розбіжність ряду.
Знаходимо границю за формулою
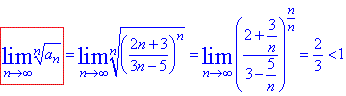
Границя менша одиниці (lim=2/3<1), тому за ознакою Коші ряд збігається.
Приклад 2. Дослідити на збіжність ряд
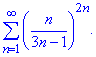
Розв'язування: Ряд знакододатний і необхідна умова збіжності виконується.
Знаходимо границю за ознакою Коші
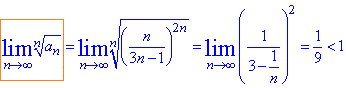
Вона менша одиниці, тому робимо висновок про збіжність ряду.
Приклад 3. Дослідити на збіжність ряд
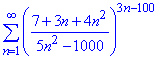
Розв'язування: Задані додатні члени ряду, які спадають з ростом номера.
Візьмемо границю кореня n-го степеня від загального члена при номері прямуючому до безмежності
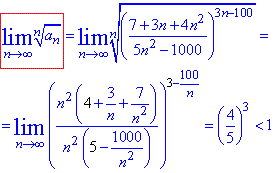
Limit=64/125<1, отже за радикальною ознакою Коші ряд збігається.
Приклад 4. Дослідити на збіжність ряд
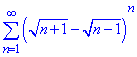
Розв'язування: Маємо різницю коренів в степені n, тому для доведення збіжності застосуємо ознаку Коші. Для розкриття границі домножуємо різницю коренів на їх суму, щоб позбутися невизначеності.
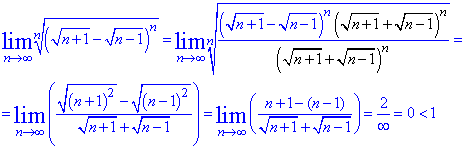
Границя рівна нулю, тому ряд збігається за ознакою Коші.
На багатьох уроках сайту знайомимо Вас з тим, як виконувати аналогічні обчислення в математичних пакетах.
В Мейплі досить вдало реалізовано обчислення границь.
Для прикладу, щоб знайти задану достатньо скомпілювати наступний код:
restart;
limit(sqrt(n+1)-sqrt(n-1), n = infinity)
В результаті отримаємо знайдену границю
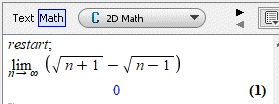
Приклад 5. Дослідити на збіжність ряд
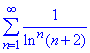
Розв'язування: Маємо ряд у вигляді дробу де в знаменнику степенева залежність від ln(n+2). Границю за радикальною ознакою Коші знайти легко.
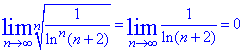
За ознакою Коші ряд збіжний.
Приклад 6. Довести, що ряд збіжний
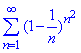
Розв'язування: Для знаходження границі зведемо загальний член ряду під другу особливу границю.
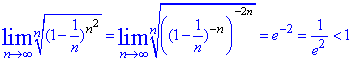
Границя менша одиниці, тому ряд за Коші збігається.
Знайдемо цю ж границю в Мейплі:
lim(((1-1/n)^(n^2))^(1/n), n = infinity);
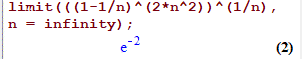
Для подальшої роботи Вам зажди стануть в нагоді знання мат. пакетів, особливо коли роботи пов'язані з обчисленнями та візуалізацією даних.
Приклад 7. Довести збіжність ряду
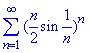
Розв'язування: Оскільки вивчаємо радикальну ознаку Коші, то зрозуміло, що її тут будемо використовувати.
Але спершу скористаємося ознакою порівняння. Для цього Ви повинні знати еквівалентні нескінченно малі величини.
Для заданого ряду
sin(1/n)≈1/n при n→∞.
Підставляємо в границю
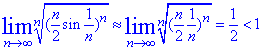
Границя =1/2<1, тому ряд збіжний.
Код для обчислення границі в Мейпл:
limit((n/2)*sin(1/n), n = infinity);
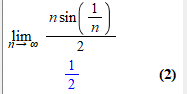
Сам хід розрахунків зашитий в ядрі програми, зате результат точно перевіряти не потрібно, оскільки розробники гарантують достовірність результатів.
Приклад 8. Дослідити на збіжність ряд
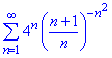
Розв'язування: При застосуванні радикальної ознаки Коші розпишемо вираз в дужках під правило другої визначної границі.
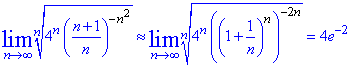
За ознакою Коші даний ряд збігається, оскільки
lim = 4/e^2≈0,55.
Приклад 9. Довести, що ряд розбігається
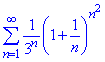
Знаходимо границю за формулою
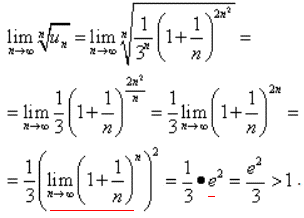
При розкритті границі використано формулу другої важливої границі.
lim=e^2/3≈2,718^2/3=2,46>1, тому за радикальною ознакою Коші ряд розбігається.
Приклад 10. Дослідити, що ряд збігається
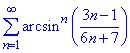
Знаходимо границю кореня n-го порядку від un=arcsinn((3n-1)/(6n+7)):
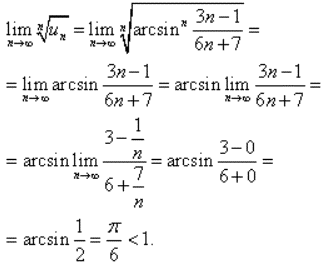
Границя π/6≈0,52(3)<1 менша одиниці, тому за ознакою Коші ряд збіжний.
З уроки Ви взнали багато нового вивчили, побачили, що без знання границь Вам непросто буде досліджувати збіжність рядів. В математиці багато тем перетинаються, і чим більше Ви будете вміти, тим легше будуть даватися для вивчення нові теми.
]]>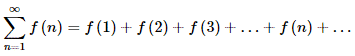
Тоді ряд f(n)=f(1)+f(2)+f(3)+…+f(n)+… збігається, якщо збіжний невластивий інтеграл
 <∞
<∞ і розбігається, якщо інтеграл прямує до безмежності
 →∞.
→∞. На практиці та в літературі часто опускають, що ця ознака також належить Макларену, тому Ви часто будете зустрічати «дослідити збіжність ряду за інтегральною ознакою Коші». Пам'ятайте, що це одна і та ж ознака збіжності.
Приклад 1. Дослідити на збіжність ряд
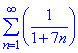
Розв'язування: Візуально бачимо, що члени ряду додатні та спадають з ростом номера. В такому випадку маємо право використати радикальну ознаку Коші для вияснення, чи ряд збіжний
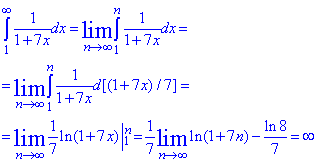
Оскільки інтеграл рівний безмежності, то ряд розбігається.
Приклад 2. Чи збіжний ряд
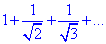
Розв'язування: З попередніх уроків Ви могли бути ознайомлені, що заданий ряд є рядом Діріхле із загальним членом an=1/√n з показником p=1/2<1, тому є розбіжним.
Доведемо це з допомогою радикальної ознаки Коші.
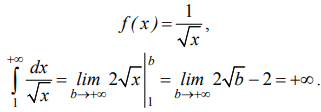
Інтеграл рівний безмежності, тому за правилом Коші він розбігається.
Приклад 3. Довести збіжність ряду
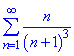
Розв'язування: Члени ряду монотонно спадають, тому необхідні умови для збіжності ряду виконуються. За достатню умову вибираємо ознаку Коші-Макларена. Для цього відповідний інтеграл розкриваємо шляхом заміни змінних
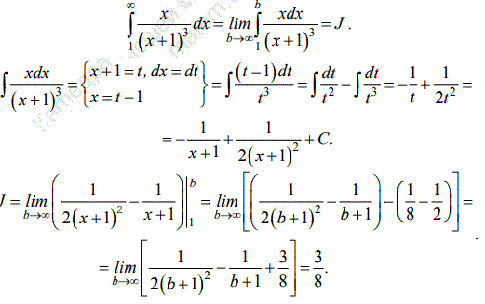
В результаті перетворень інтеграл int=3/8 скінченний, тому за інтегральною ознакою він збігається.
Приклад 4. Довести, що ряд розбігається
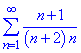
Розв'язування: Члени ряду по характеру збіжності можна порівняти з гармонійним рядом і довести, що він розбіжний. Але так як мета уроку, навчити Вас застосовувати інтегральну ознаку Коші, то переходимо до інтегрування відповідної ряду функції:
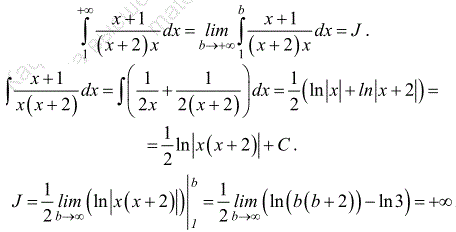
Інтеграл рівний безмежності, що є признаком розбіжності ряду.
Приклад 5. Дослідити на збіжність ряд
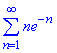
Розв'язування: Візуально бачимо лише, що члени ряду додатні:
експонента у від'ємному степені прямує до нуля.
Чи ряд спадає стане ясно лише з підстановки номерів, тому цей крок опустимо і перейдемо до перевірки чому рівний інтеграл.
Інтегруємо частинами
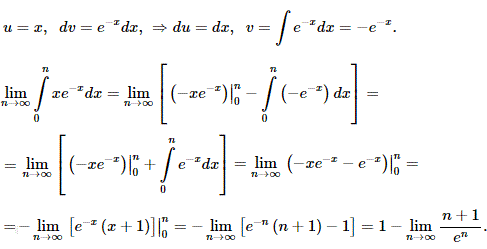
До останнього доданку застосовуємо правило Лопіталя
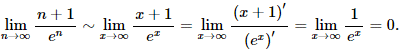
При підстановці в попередню формулу отримаємо інтеграл рівний 1, отже ряд за інтегральною ознакою збігається.
Приклад 6. За допомогою радикальної ознаки Коші довести, що ряд збіжний
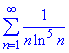
Розв'язування: Бачимо, що задано додатний спадний ряд з загальним членом
un=1/(n•ln^5(n)).
За інтегральною ознакою Коші знаходимо невластивий інтеграл.
Для розкриття інтегралу «ікс» зі знаменника вносимо під диференціал dx/x=d(ln(x)):
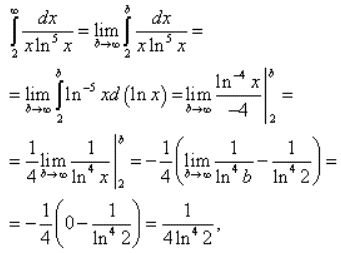
Інтеграл збіжний, отже за ознакою Коші ряд також збіжний, що і потрібно було довести.
Приклад 7. Чи збігається ряд

Розв'язування: Оскільки функція f(n)=1/(2n+3)^(7/6) визначена для всіх n≥1, додатна і спадна, то застосуємо інтегральну ознаку Коші збіжності ряду
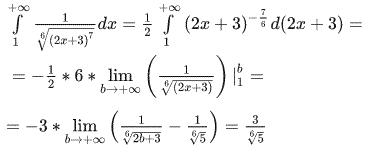
Оскільки інтеграл скінченний, то за Коші він збіжний.
Приклад 8. Дослідити на збіжність ряд
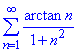
Розв'язування: Слід знати область значень оберненої тригонометричної функції арктангенс, щоб оцінити чисельник зверху:
arctan(n)<π/2.
Тоді за ознакою порівняння отримаємо
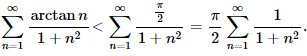
Застосовуючи інтегральну ознаку Коші, оцінимо збіжність ряду
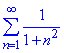
Відповідний інтеграл знаходимо шляхом внесення знаменника під диференціал
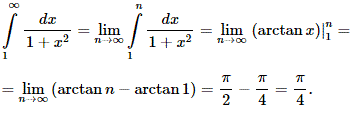
Оскільки невластивий інтеграл збіжний, то заданий ряд також збіжний.
На практиці Ви зустрінете малу кількість рядів, збіжність яких доцільно доводити за інтегральною ознакою збіжності. Такі ряди, як правило, легко інтегруються. Вивчіть інтегральну ознаку збіжності та використовуйте там де потрібно.
]]>Ряд вигляду
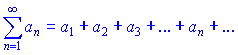
називається знакозмінним, якщо частина його членів приймає додатні значення, а решта - від'ємні.
Знакопочерговим називається ряд, сусідні члени якого мають протилежні знаки. У випадку, коли перший член знакопочергового ряду додатний, його можна подити у вигляді
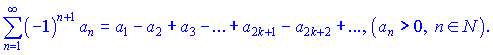
Ознака Лейбніца
Для дослідження збіжності ряду використовують ознаку Лейбніца: якщо члени знакопочергового ряду спадають по абсолютній величині та границя загального члена ряду рівна нулю
![]()
то ряд збіжний. При цьому сума ряду не перевищує значення його першого члена, якщо він додатній.
Для знакозмінного ряду існують поняття абсолютної та відносної збіжності.
Знакозмінний (знакопочережний) ряд збіжний абсолютно, якщо цей ряд та ряд утворений з модулів членів цього ряду збіжні одночасно.
Ряд називають умовно або неабсолютно збіжним у випадках, коли збіжний лише знакозмінний ряд, а ряд складений з абсолютних величин членів ряду розбігається.
Дослідження рядів на збіжність
Приклад 1. Дослідити які ряди збігаються абсолютно, умовно чи розбігаються
1) (9.131)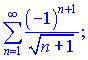
Розв'язок. Даний ряд знакопочережний, а також кожен наступний член по модулю менший за попередній
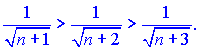
Знайдемо границю загального члену ряду
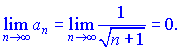
За ознакою Лейбніца ряд збіжний. Перевіримо ряд складений з модулів членів на абсолютну збіжність. Застосуємо ознаку Даламбера
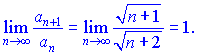
Дана ознака відповіді не дає. Застосуємо інтегральну ознаку Коші
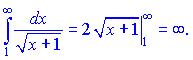
Ряд розбіжний, інтеграл рівний безмежності.
Оскільки знакопочережний ряд збіжний, а ряд з модулів розбіжний, то роглянутий ряд відносно збіжний.
2) (9.132)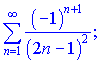
Розв'язок. Кожен наступний член ряду по модулю менший за попередній
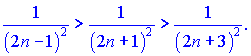
Границя загального члена рівна нулеві
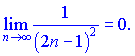
Ознака Лейбніца виконується.
Перевіримо ряд на абсолютну збіжність. Застосуємо інтегральну ознаку Коші
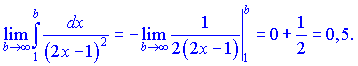
Вона підтверджує збіжність ряду. Вихідний ряд абсолютно збіжний.
3) (9.133)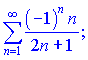
Розв'язок. Необхідна ознака збіжності не виконується, оскільки кожен наступний член ряду по модулю більший за попередній
![]()
За озакою Лейбніца ряд розбігається.
4) (9.134)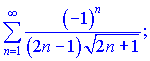
Розв'язок. Члени ряду по модулю спадають
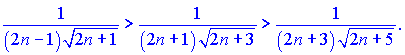
Обчислюємо границю un
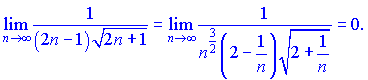
Границя рівна нулю, отже ряд збіжний за ознакою Лейбніца.
Перевіримо на абсолютну збіжність. З вигляду бачимо, що ознака Делабера нічого не дасть. Застосуємо інтегральну ознаку Коші. Після заміни змінних під інтегралом отримаємо гіперболічний арктангенс, який на межах інтегрування приймає обмежене значення
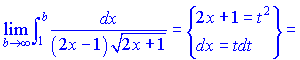
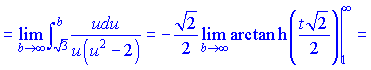
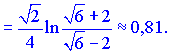
Даний ряд збіжний (Integal=0,81). Отже ряд абсолютно збіжний.
Приклад 2. Дослідити знакочережний ряд на збіжність.
а) 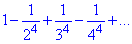
Маємо 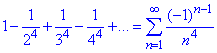
Нехай cn=1/n^4. Досліджувати цей ряд будемо за ознакою Лейбніца:
ряд 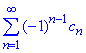 збігається, якщо границя n-го члена рівна нулю
збігається, якщо границя n-го члена рівна нулю 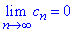 і cn>cn+1>0.
і cn>cn+1>0.
Перевірка показує, що умови виконуються
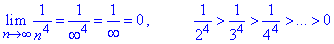
звідси слідує, що ряд 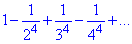 збігається.
збігається.
б) 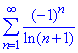
Досліджувати цей ряд будемо за ознакою Лейбніца:
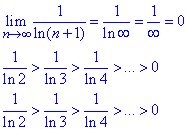
звідси слідує, що ряд 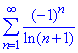 збігається, але умовно, бо ряд складений за модулем
збігається, але умовно, бо ряд складений за модулем 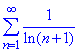 розбіжний.
розбіжний.
На цьому ознайомлення з ознакою Лейбніца завершено. Разом з ознаками для додатніх рядів Ви тепер можете перевіряти знакопочергові ряди на абсоюту збіжність. Впереді Вас чекає маса уроків, які в повній мірі дозволять Вам аналізувати та досліджувати числові та функціональні ряди.
]]>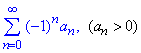 називається знакозмінним або знакопочережним рядом.
називається знакозмінним або знакопочережним рядом. 
Ознака Лейбніца: Якщо члени знакопочергового ряду спадають за абсолютною величиною і границя абсолютної величини загального члена ряду дорівнює нулю, то ряд збігається
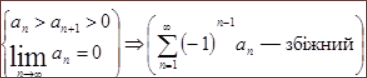
Знакозмінні ряди. Абсолютна та умовна збіжність
Теорема (Коші): Якщо ряд із модулів членів ряду збіжний |un|, то знакозмінний ряд також збіжний.
Означення 1: Знакозмінний ряд 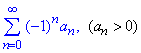 називається абсолютно збіжним, якщо збіжний ряд складений із модулів членів знакозмінного ряду.
називається абсолютно збіжним, якщо збіжний ряд складений із модулів членів знакозмінного ряду.
Означення 2: Якщо ряд складений із модулів знакозмінного ряду розбіжний, а сам знакозмінний ряд збіжний, то така збіжність називається умовною, а ряд умовно збіжним.
Приклади дослідження збіжності ряду
Приклад 1. Дослідити збіжність ряду
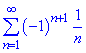
Розв'язування: Даний ряд є знакозмінним рядом, кожен його наступний член по модулю 1/n<1/(n+1)<... менший за попередній, границя при номері прямуючому до безмежності прямує до нуля.
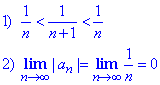
За ознакою Лейбніца знакозмінний ряд збіжний, хоча ряд складений із модулів представляє собою гармонійний ряд 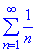 , який розбіжний, тому досліджений ряд умовно збіжний.
, який розбіжний, тому досліджений ряд умовно збіжний.
Приклад 2. Дослідити ряд
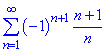
Розв'язування: Перевіряємо необхідні умови збіжності ряду
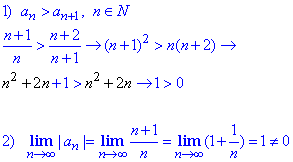
Перша умова виконується – члени ряду з модулів монотонно спадають. Однак границя модуля загального члена ряду не прямує до нуля при прямуванні номера до безмежності, тому ряд за ознакою Лейбнца розбіжний.
Приклад 3. Дослідити збіжність ряду
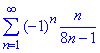
Розв'язування: Ряд монотонно спадає 1/7>2/15>3/23>…
Перша з необхідних умов збіжності знакозмінного ряду виконується.
Обчислимо границю
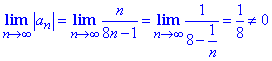
За ознакою Лейбніца ряд розбіжний, границя n-го члена по модулю не прямує до нуля при номері прямуючому до безмежності.
Приклад 4. Дослідити на умовну та абсолютну збіжність ряд
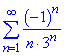
Розв'язування: 1) Легко переконатися, що кожний наступний член ряду по модулю 1/(n*3^n) менший за попередній.
1/3>1/18>1/243…
2) Для визначення абсолютної збіжності ряду застосуємо ознаку Даламбера
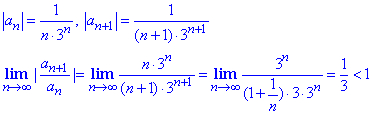
Границя відношення сусідніх членів ряду за модулем менша одиниці, отже ряд складений з модулів за ознакою Даламбера збіжний.
Звідси слідує, що заданий знакозмінний ряд абсолютно збіжний.
Приклад 5. Дослідити ряд збіжність
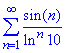
Розв'язування: В залежності від n синус приймає як від'ємні так і додатні значення, тому даний ряд є знакозмінним.
Оцінимо загальний член ряду по модулю
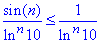
Ряд 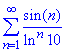 збіжний, як геометричний ряд 1/q^n з основою q=1/ln10<1.
збіжний, як геометричний ряд 1/q^n з основою q=1/ln10<1.
Оскільки ряд із модулів збіжний за ознакою ознакою порівняння, то заданий ряд збіжний, причому абсолютно.
Приклад 6. Довести, що ряд збіжний умовно
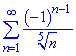
Розв'язування: Легко переконатися, що члени ряду за модулем спадають.
Границя загального члена ряду за модулем прямує до нуля
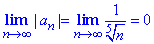
тому за ознакою Лейбніца ряд збіжний.
Ряд складений із модулів заданого ряду із загальним членом un=1/n^1/5 є рядом Діріхле зі степенем p=1/5<1, тому він є розбіжним. Якщо абсолютний ряд розбіжний, а знакозмінний ряд збіжний, то він збіжний умовно, що і слід було довести.
Як висновок з цього прикладу, можна вказати, що всі знакозмінні ряди, які за модулем можна порівняти з рядом Діріхле вигляду 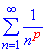 будуть абсолютно збіжними, якщо p>1.
будуть абсолютно збіжними, якщо p>1.
Тобто, якщо ряд з модулів спадає трохи швидше за гармонічний ряд an=1/n то такий знакозмінний ряд абсолютно збіжний.
Приклад 7. Довести збіжність ряду 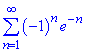
Розв'язування: Кожний наступний член ряду складеного з модулів менший за попередній
1/e>1/e^2>1/e^3…
Границя n-го члена ряду прямує до нуля
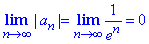
тому за ознакою Лейбніца знакозмінний ряд збіжний.
Для дослідження на абсолютну збіжність застосуємо радикальну ознаку Коші
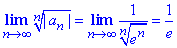
Зауважте, що вона ефективна лише у випадках коли члени ряду можна представити як певну скінченну величину в степені n.
Оскільки одиниця розділити на експоненту менша за одиницю 1/e<1, то границя менша одиниці, отже абсолютний ряд збіжний.
Звідси слідує, що знакозмінний ряд абсолютно збіжний.
Приклад 8. Дослідити на абсолютну збіжність ряд
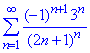
Розв'язування: Бачимо, що ряд з модулів монотонно спадає
1>9/25>81/343>…
Знайдемо границю на нескінченності
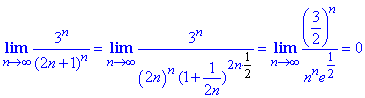
Тут частину знаменника звели під другу чудову границю =e.
Для перевірки на абсолютну збіжність застосуємо ознаку Даламбера
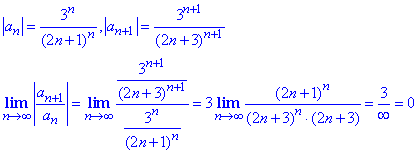
Аналогічний результат отримаємо за радикальною ознакою Коші
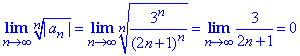
Абсолютний ряд збіжний, тому робимо висновок, що знакозмінний ряд абсолютно збіжний.
Застосовуйте наведену схему для доведення збіжності рядів за Лейбніцом, якщо буде важко, звертайтесь за допомогою.
В наступному уроці розберемо приклади на обчислення суми знакозмінного ряду з заданою точністю та дослідження рядів на збіжність.
Необхідна умова збіжності ряду: Якщо границя загального члена ряду не прямує до нуля при номері прямуючому до безмежності то ряд є розбіжним.
Якщо ця умова виконується, то ще не факт, що ряд збігається, потрібно застосовувати одну з розглянутих далі ознак збіжності числових рядів.
Приклад 1. Дослідити на збіжність ряд
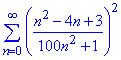
Розв'язування: Перш ніж переходити до певної ознаки збіжності ряду слід переконатися (візуально), що загальний член ряду прямує до нуля.
Знайдемо границю an:
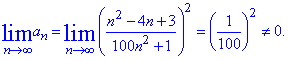
Оскільки загальний член ряду прямує до 1/100^2≠0, то необхідна умова збіжності ряду не виконується. Тому ряд розбіжний.
Приклад 2. Дослідити на збіжність ряд
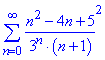
Розв'язування: Запам'ятайте: якщо ряд має вигляд дробу де в чисельнику чи знаменнику є степеневі функції або факторіали, то потрібно застосовувати ознаку Даламбера:
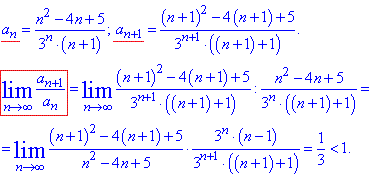
Границя дорівнює 1/3<1, отже ряд збігається.
Приклад 3. Дослідити на збіжність ряд
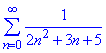
Розв'язування: Застосуємо граничну ознаку порівняння.
З теорії відомо, що будь-який ряд який спадає швидше за гармонійний bn=1/n є збіжний.
В нашому випадку порівняємо зі збіжним узагальненим гармонійним рядом вигляду
cn=1/n^2, де показник степеня a=2>1.
Обчислимо відношення n-х членів при номері, що прямує до безмежності
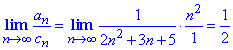
Оскільки границя існує (=1/2) і скінченна, то обидва ряди є збіжними, що і треба було встановити.
Приклад 4. Дослідити на збіжність ряд
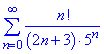
Розв'язування: За правилом Даламбера знаходимо границю
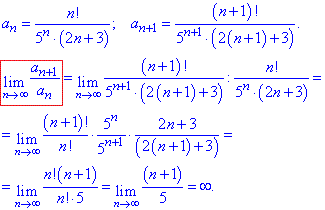
Границя нескінченна, тому ряд розбігається.
Приклад 5. Дослідити на збіжність ряд та знайти його суму
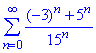
Розв'язування: Загальний член ряд можна спростити, розділивши почленно чисельник на знаменник
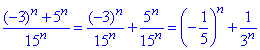
В такий спосіб ряд замінили сумою двох збіжних геометричних рядів
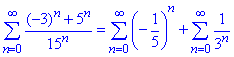
Можна доводити збіжність окремо взятого ряду, проте і так видно характер їх спадання.
За формулою суми геометричного ряду обчислюємо суму заданого
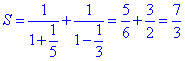
Остаточно, ряд збіжний і його сума дорівнює 7/3.
Приклад 6. Дослідити збіжність ряду
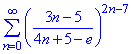
Розв'язування: Якщо бачите, що ряд має вигляд дробу піднесеного в певному степені, що залежить від n, то можете сміло використовувати радикальну ознаку Коші:
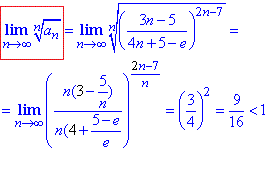
Якщо границя менша одиниці, то ряд збіжний.
В нас границя 9/16 менша одиниці, тому ряд збігається.
Приклад 7. Загальний член ряду задано формулою
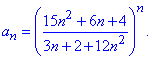
Довести розбіжність ряду.
Розв'язування: Застосуємо радикальну ознаку Коші
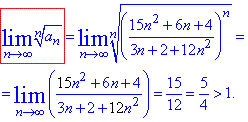
Границя =15/12>1, тому робимо висновок про розбіжність ряду.
Приклад 8. Дослідити збіжність ряду
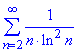
Розв'язування: Дослідимо ряд з допомогою інтегральної ознаки Коші.
На практиці її застосовують вкрай рідко, але Ви повинні знати її та вміти користуватися.
Для цього випишемо відповідний інтеграл до ряду та, методом заміни змінних, знайдемо його значення
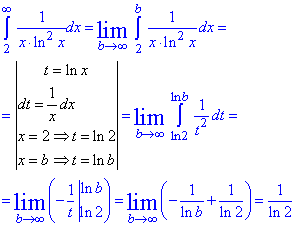
Уважно співставте змінні в інтегралі та межі з тим, що маємо в ряді.
n - заміняємо "іксом", межі — початок та кінець лічильника ряду.
Інтеграл (=1/ln2) скінченний, отже ряд також збігається.
Приклад 9. Дослідити на збіжність
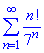
Розв'язування: В чисельнику маємо факторіал функцію в знаменнику степеневу, тому найпростіше тут застосувати ознаку Даламбера
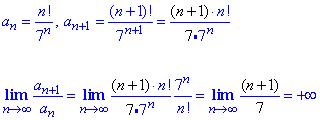
Границя відношення наступного члена ряду до попереднього нескінченна, тому за ознакою Даламбера ряд розбігається.
Приклад 10. Довести, що ряд розбігається
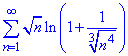
Розв'язування: Спершу перетворимо загальний член ряду.
Оскільки під логарифмом маємо 1+ нескінченно малу величину, то логарифм такого виразу рівний еквівалентній нескінченно малій величині
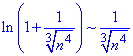
Далі ряд заміняємо еквівалентним
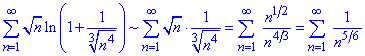
Отримали узагальнений гармонійний ряд з показником p=5/6<1, який є розбіжний. Тому заданий ряд, з якого отримали узагальнений гармонійний ряд, також розбігається.
Приклад 11. Довести збіжність ряду
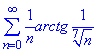
Розв'язування: При n→∞ арктангенс нескінченно малої величини має характер самої величини, тому доцільно застосувати ознаку порівняння
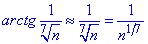
При обчисленні границі
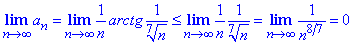
отримаємо ряд Діріхле з показником p=8/7>1.
Він швидше спадає ніж гармонічний ряд, тому є збіжним.
Приклад 12. Чи збіжний ряд
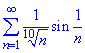
Розв'язування: Тут застосуємо метод порівняння.
При n→∞ синус від нескінченно малої величини замінюємо малою величиною sin(1/n)≈1/n.
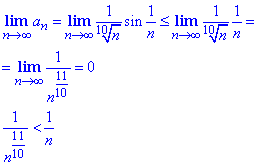
Отримали ряд Діріхле з показником p=11/10>1, він швидше спадає за гармонічний ряд.
Оскільки члени отриманого ряду швидше спадають за члени гармонічного (є розбіжним), то заданий ряд збігається.
Приклад 13. Дослідити на збіжність ряд
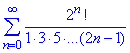
Розв'язування: В таких завданнях часто допускають помилку, виписуючи наступний член ряду для ознаки Даламбера.
Суть полягає в тому, що знаменник подають у вигляді
1•3•5•…(2(n+1)-1)=1•3•5•…(2n+1)
гублячи при цьому попередній множник.
Зверніть на це увагу і візьміть за правило подавати наступний член через попередній
1•3•5•…(2n-1)(2(n+1)-1)=
= 1•3•5•…(2n-1)(2n+1).
Тоді при знаходженні границі наступного члена ряду до попереднього
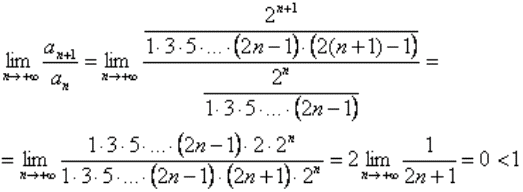
отримаєте коректне значення.
Приклад 14. Дослідити на збіжність ряд
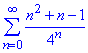
Розв'язування: В знаменнику загального члена ряду маємо степеневу функцію 4^n, тому це нас спонукає до застосування формули Даламбера
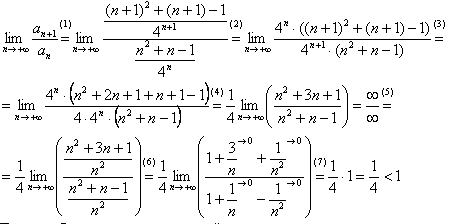
Границя менша одиниці, тому за правилом Даламбера ряд збігається.
Приклад 15. Дослідити на збіжність ряд
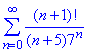
Розв'язування: Для дослідження збіжності скористаємося ознакою Даламбера:
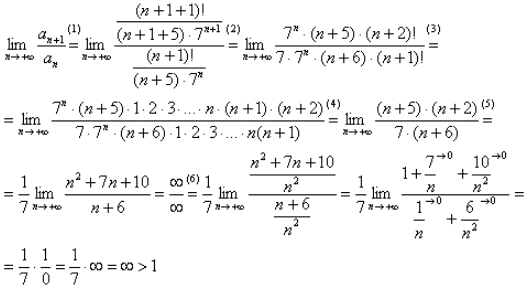
Оскільки границя нескінченна, то ряд розбігається.
Приклад 16. Довести збіжність ряду
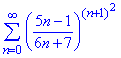
Розв'язування: Тут можна повозитися з ознакою Даламбера, але швидше можна отримати результат, якщо використати радикальну ознаку Коші.
Беремо границю кореня n-го порядку від загального члена та розписуємо
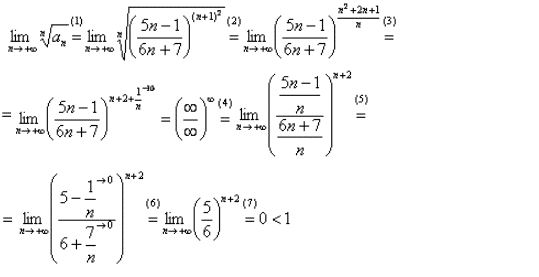
Границя менша одиниці, тому ряд збігається.
Більше готових прикладів та детальних пояснень до ознак збіжності ряду Ви знайдете на сусідніх сторінках сайту. Ми постійно допомагаємо студентам, тому відповідей до завдань на ряди попереду ще багато.
"Практикуйте самостійно!" - це найкраща порада, яка в швидкому часі принесе Вам хороші результати.
Приклад: 3.6 Знайти радіус збіжності та область збіжності степеневих рядів:
а) 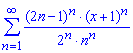
Обчислення: Для оцінки складемо ряд із модулів членів заданого ряду, тобто ряд із наступним загальним членом
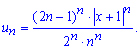
Далі, так як отриманий ряд має додатні члени, то досліджувати його на збіжність будемо за допомогою ознаки Даламбера:
![]()
Для цього виписуємо наступний до загального член ряду
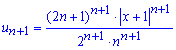
та підставляємо в формулу границі. Вигляд членів ряду непростий, тому будьте уважні при розписуванні границі
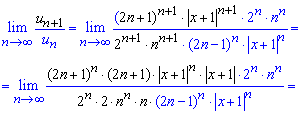
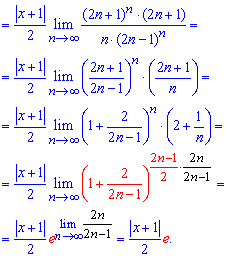
Вкінці приходимо до експоненти та функціонального множника.
Якщо границя менша одиниці,
![]()
то ряд збігається за теоремою Даламбера.
Звідси складаємо обмеження на допустимі "ікси"
![]()
![]() - область збіжності.
- область збіжності.
Отже знайшли ![]() - радіус збіжності та
- радіус збіжності та
![]() - область збіжності ряду.
- область збіжності ряду.
Для себе запам'ятайте, що радіус збіжності рівний половині відстані між крайніми точками області збіжності.
б) ![]()
Обчислення: Складемо ряд із модулів членів заданого ряду, тобто із загальним членом
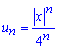
Ми отримали ряд з додатними членами, тому можемо досліджувати його на збіжність за допомогою ознаки Даламбера.
Для цього записуємо наступний член ряду
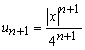
та підставляємо в границю
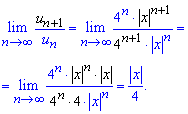
При границі меншій одиниці ![]() - ряд збігається за теоремою Даламбера.
- ряд збігається за теоремою Даламбера.
З цієї умови знаходимо
![]() - область збіжності.
- область збіжності.
Таким чином, ми знайшли R=4 - радіус збіжності ряду, та область збіжності ![]() .
.
Приклад: 3.11 Знайти радіус збіжності та область збіжності степеневих рядів:
а) 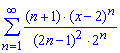
Обчислення: Члени заданого функціонального ряду
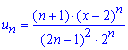
визначені на всій дійсній осі ![]() , тобто область визначення наступна
, тобто область визначення наступна
![]() .
.
Складемо ряд із модулів членів заданого ряду:
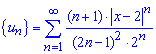 ,
,
Його загальний член має формулу
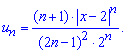
Оскільки новий ряд має додатні члени, то досліджувати на збіжність будемо за ознакою Даламбера:
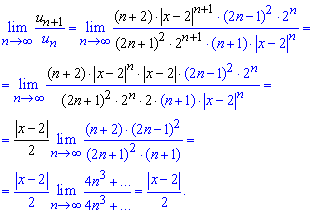
При ![]() - ряд збігається за теоремою Даламбера, тобто необхідно, щоб виконувалися умови
- ряд збігається за теоремою Даламбера, тобто необхідно, щоб виконувалися умови
![]()
Звідси знаходимо R=2 – радіус збіжності ряду та (0; 4) - область збіжності.
б) 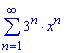
Обчислення: Члени заданого функціонального ряду
![]()
визначені при ![]() , тобто область визначення наступна
, тобто область визначення наступна
![]() .
.
Складемо ряд із модулів членів заданого ряду:
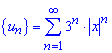
Для дослідження ряду на збіжність використаємо ознаку Даламбера:
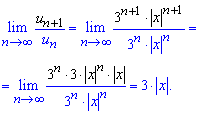
За теоремою Даламбера при границі меншій за одиницю ![]() - ряд збігається.
- ряд збігається.
Звідси знаходимо область збіжності
![]()
та R=1/3 радіус збіжності. Із наведених прикладів
Ви могли побачити таку закономірність, що значення, що обмежує модуль є радіусом збіжності ряду.
Область збіжності має в два рази більшу довжину і визначається розкриттям модуля.
Приклад: 3.17 Знайти радіус збіжності та область збіжності степеневих рядів:
а) 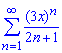
Обчислення: Члени заданого функціонального ряду
![]()
визначені при всіх дійсних аргументах 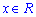 , тобто
, тобто ![]() .
.
Складемо ряд із модулів членів заданого ряду:
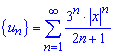 ,
,
тобто
![]()
Оскільки даний ряд має додатні члени, то досліджувати його на збіжність будемо за допомогою ознаки Даламбера. Виписуємо наступний за загальним член ряду
![]()
та підставляємо у границю
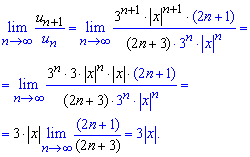
При 3|x|<1 - ряд збігається,
тобто
![]() – область збіжності.
– область збіжності.
Все, що справа від модуля це R=1/3 – радіус збіжності ряду, а обмеження на "ікс"
![]() – це область збіжності.
– це область збіжності.
б) 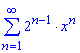
Обчислення: Члени функціонального ряду
![]()
визначені на всій дійсній множині ![]() , їх область визначення
, їх область визначення ![]() .
.
Складемо ряд із модулів членів заданого ряду:
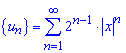
що мають наступний загальний член
![]()
Утворений ряд будемо досліджувати на збіжність за ознакою Даламбера:
Для цього записуємо наступний член, що йде після загального
![]()
та підставляємо у границю
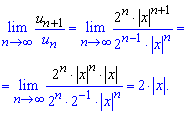
При 2|x|- ряд буде збіжним за Даламбером.
Розкриваємо модуль і знаходимо
![]() – область збіжності.
– область збіжності.
та R=1/2 – радіус збіжності.
У вигляді інтервалу записуємо область збіжності
![]()
Приклад: 3.27 Знайти радіус збіжності та область збіжності степеневого ряду:
а) 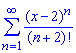
Обчислення: Члени функціонального ряду 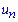 визначені на дійсній осі
визначені на дійсній осі ![]()
Складемо ряд із модулів членів цього ряду:
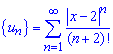
Загальний член задається формулою
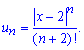
Досліджувати ряд із модулів на збіжність будемо за допомогою ознаки Даламбера:
Записуємо наступний член
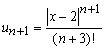
та знаходимо границю
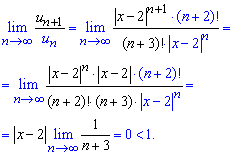
Оскільки A=0<1, то ряд збігається (за теоремою Даламбера) при всіх дійсних змінних ![]() , тобто має необмежену
, тобто має необмежену ![]() - область збіжності.
- область збіжності.
Ряд має безмежний ![]() - радіус збіжності.
- радіус збіжності.
б) 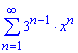
Обчислення: Члени ряду ![]() визначені на множині дійсних чисел
визначені на множині дійсних чисел
![]()
Побудуємо ряд із модулів членів ряду:
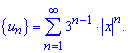
Далі записуємо загальний та наступний після нього член ряду
![]()
та підставляємо у границю
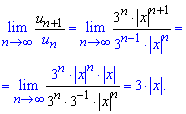
За теоремою Даламбера ряд збігається при 3|x|. З цієї умови визначаємо
![]() – область збіжності ряду
– область збіжності ряду
та R=1/3 – радіус збіжності.
У вигляді інтервалу область збіжності матиме запис ![]() .
.
Приклад 3. Дослідити функціональний ряд на збіжність.
а) 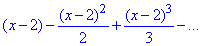
Для степеневого ряду виду
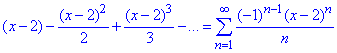
випишемо загальний член 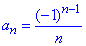 і x0=2.
і x0=2.
Знайдемо радіус збіжності степеневого ряду за формулою:
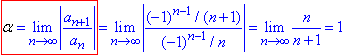
звідси R=1.
Область збіжності ряду:
x∈(-1;1).
Підсумовуємо, що ряд 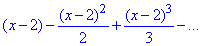 збігається, якщо x∈(-1;1).
збігається, якщо x∈(-1;1).
б) an=xn/(n+3)
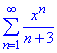
Маємо степеневий ряд виду
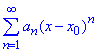 , де an=1/(n+3), x0=0.
, де an=1/(n+3), x0=0.
Знайдемо радіус збіжності степеневого ряду:
R=1/α, де
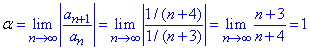
звідси R=1.
Ряд збігається на інтервалі:
x∈(-1;1).
Тепер Ви знаєте як знайти область збіжності та радіус збіжності ряду. Користуйтеся наведеними формулами та успішної Вам здачі сесії.
Готові розв'язки на ряди:
]]>
Наслідком з теорем Абеля є те, що при "іксах" менших радіуса збіжності R ряд абсолютно збіжний, при |x|>R ряд розбігається і при x=-R, x=R потрібні додаткові дослідження. Більше теорії про радіус збіжності та область збіжності степеневих рядів Ви можете ознайомитися за посиланням. Нижче приведені формули радіуса збіжності ряду за ознакою Д'Аламбера та радикальною ознакою Коші.

Переходимо до практичних та детально пройдемо алгоритм знаходження радіуса степеневого ряду, а за ним і самої області збіжності.
Приклад 1. Знайти область збіжності степеневого ряду
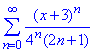
Розв'язування: Виписуємо два послідовних члени ряду, підставляємо в формулу області збіжності та розписуємо границю за д'Аламбером
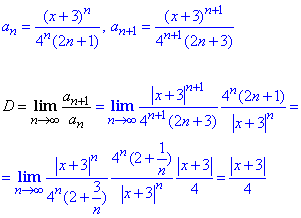
Згідно з теорією, отримана границя за модулем повинна бути менша одиниці
|x+3|/4<1,
|x+3| -4<x+3<4
-4-3<x<4-3
-7<x<1
x∈(-7;1) – область збіжності степеневого ряду.
Окремо слід розібрати граничні випадки.
При x=1 отримаємо ряд близький за поведінкою до гармонічного (an=1/n), тому він розбіжний.
При x=-7 загальний член заданого ряду набуде вигляду
bn=(-1)n/(2n+1).
Члени ряду з модулів монотонно спадають + границя n-го члена прямує до нуля, тому за ознакою Лейбніца він збіжний.
Ця збіжність не абсолютна, а умовна, оскільки ряд складений з модулів розбіжний.
Тому остаточно у відповідь слід записати
x∈[-7;1) – область збіжності степеневого ряду.
Приклад 2. Визначити радіус збіжності та область збіжності функціонального ряду
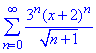
Розв'язування: Повторюємо алгоритм обчислень
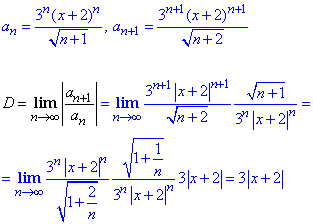
За формулою Даламбера, щоб ряд був збіжним, необхідно щоб знайдена границя по модулю не перевищувала 1.
Звідси розписуємо нерівність з модулем
3|x+2|<1,
|3x+6|<1,
-1<3x+6<1,
-1-6<3x<1,
-6 -7<3x<-5,
-7/3<x<-5/3.
x∈(-7/3;-5/3).
Перевіримо крайні точки.
При x=-5/3 загальний член ряду перетворюєтья до вигляду an=1/√(n+1), що є рядом Діріхле з показником степеня p=1/2<1.
Тому такий числовий ряд розбіжний.
При x=-7/3 отримаємо знакозмінний ряд an=(-1)n+1/√(n+1), який за модулем монотонно спадає і прямує до нуля при спрямуванні номера до безмежності.
Такий ряд за ознакою Лейбніца є збіжним.
Радіус збіжності рівний R=(-5/3+7/3)/2=1/3,
x∈[-7/3;-5/3) – область збіжності функціонального ряду.
Це найповніше обґрунтування до умови прикладу.
Приклад 3. Визначити область збіжності ряду
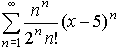
Розв'язування: Запишемо загальний вигляд степеневого ряду
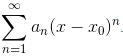
Центр області збіжності x0=5.
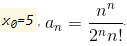
Область збіжності степеневого ряду визначається радіусом збіжності R:
|x-x0|<R або x0-R<x<x0+R
Збіжність ряду на границях (при x=x0±R) необхідно досліджувати додатково.
Знайдемо радіус збіжності ряду за формулою д'Аламбера:
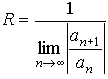
Виписуємо члени ряду та знаходимо границю їх відношення
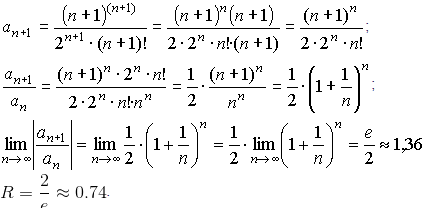
Перевіримо збіжність ряду на правому краю
x=5+2/e.
Підстановкою x в заданий ряд, отримаємо
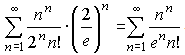
Для дослідження ряду використаємо формулу Стірлінга , справедливу для факторіалів великих чисел
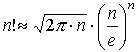
Отримаємо ряд для застосування ознаки порівняння, який є розбіжним
Дослідимо збіжність ряду при x=5-2/e.
При підстановці x=5-2/e в 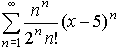 отримаємо знакозмінний числовий ряд
отримаємо знакозмінний числовий ряд
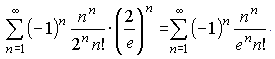
При застосуванні формули Стірлінга дістанемо ряд для порівняння
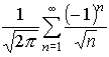
Цей ряд є збіжним за ознакою Лейбніца, хоча й умовно, оскільки для ряду з модулів степінь знаменника p=1/2<1, тому абсолютний ряд розбігається.
Тому ліву границю включаємо в область збіжності степеневого ряду:
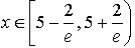
Запам'ятайте, що найшвидше перевірити збіжність ряду можна на лівій границі області. Якщо в ній отриманий знакозміннний ряд умовно збіжний, то цю точку включаємо, а праву границю не включаємо
x0-R≤x<x0+R .
Якщо на лівій границі області збіжності ряд абсолютно збіжний то праву границю також включаємо
x0-R≤x≤x0+R.
Приклад 4. Довести, що радіус збіжності ряду рівний 5/3 та визначити чи входять краї в область збіжності ряду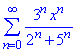
Розв'язування: За формулою Даламбера знаходимо радіус збіжності
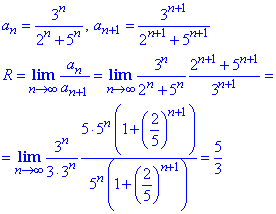
Таким чином отримали R=5/3, і степеневий ряд абсолютно збіжний на інтервалі (-5/3;5/3).
перевіримо збіжність на краях.
Для цього дослідимо лівий край x=-5/3.
При підстановці вихідний ряд прийме вигляд
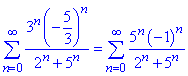
Отриманий знакозмінний ряд монотонно спадає за абсолютною величиною, однак не прямує до нуля при змінній прямуючій до безмежності
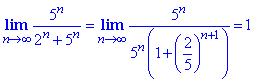
За ознакою Лейбніца ряд розбіжний.
Таку ж границю отримаємо на правому краю області збіжності.
Звідси робимо висновок, що крайні точки не входять в область збіжності ряду.
Остаточно отримали, що степеневий ряд збіжний в інтервалі
x∈(-5/3;5/3).
На цьому всі доведення та дослідження до умови виконані.
Приклад 5. Знайти область збіжності ряду
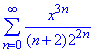
Розв'язування: До ряду складеного з модулів an=x^3n/((n+1)*2^2n) застосуємо ознаку Даламбера:
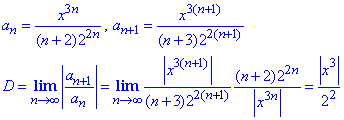
При |x|^3/4<1 степеневий ряд збігається абсолютно.
Звідси випливає, що радіус збіжності рівний коренію кубічному з чотирьох
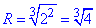 , а інтервалом збіжності ряду є
, а інтервалом збіжності ряду є 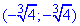
На кінцях інтервалу збіжності:
при 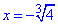 запишемо чому рівний ряд
запишемо чому рівний ряд
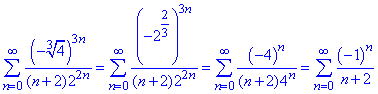
Це знакозмінний ряд, який за модулем монотонно збігається і границя n-го члена прямує до нуля, тому за ознакою Лейбніца ряд збіжний.
Ця збіжність умовна, тому що ряд складений з модулів un=1/(n+2) розбігається як гармонічний ряд.
Тому лівий край в область збіжності степеневого ряду включаємо, а правий ні:
Остаточно, 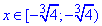 - область збіжності степеневого ряду.
- область збіжності степеневого ряду.
Якщо б викладач питав, чому так, то слід обґрунтувати, що умовної збіжності за Лейбніцом достатньо, щоб включити ліву границю області збіжності в розв'язок.
Таких прикладів ми розв'язуємо десятками, допомагаючи студентам на екзаменах та розрахункових. Крок за кроком вивчайте наведені в категорії Ряди теми і з часом у Вас не буде питань на практичних чи іспитах.
]]>