Подібні завдання на системи диференціальних рівнянь можуть бути задані на контрольній роботі. Перше завдання містить систему двох однорідних рівнянь, друге - систему двох неоднорідних рівнянь. Завдання розв'язані через характеристичне рівняння і без нього, це дає можливість показати Вам переваги кожного з методів. Яким методом краще рішати завдання вибирати Вам, тож не гайте часу і вчіться.
Приклад 7. Розв'язати системи диференціальних рівнянь
а) 
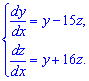
Обчислення: Розв'яжемо характеристичне рівняння
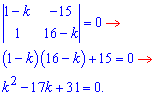
Отримане квадратне рівняння обчислюємо через дискримінант
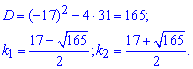
Складемо систему для знаходження чисел γ1 i γ2 , якi вiдповiдають числу k1 Матрицю коефiцiєнтiв цiєї системи отримуємо з матриці
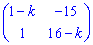
замiною k на k1.
Отже, шуканою системою є
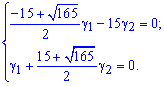
Нехай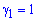 
, тоді
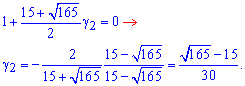
Таким чином, характеристичному числу
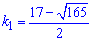
вiдповiдає розв'язок
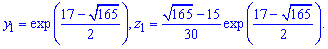
Аналогічним чином, розв'язуємо систему
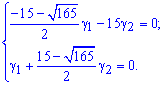
яка відповідає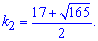 
Поклавши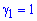 
з другого рівняння знаходимо
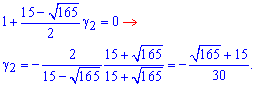
Таким чином, другому числу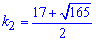 
відповідає розв'язок
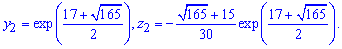
Загальний розв'язок системи ДР записуємо через лінійну комбінацію сталих на знайдені функції
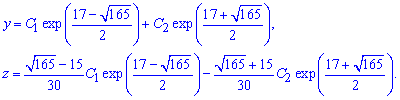
На цьому систему диференціальних рівнянь розв'язано.
б) 
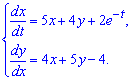
Обчислення: Відповідну однорідну систему рівнянь
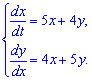
зінтегруємо методом виключення.
З першого рівняння виразимо y
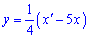
та підставимо у друге
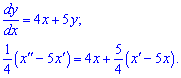
Множимо на 4 і переносимо все в одну сторону
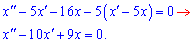
Відповідне характеристичне рівняння матиме вигляд
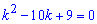
а його корені
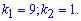
Можемо записати розв'язок однорідного ДР
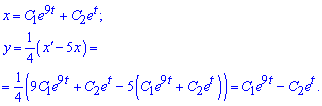
Розв'язок заданої неоднорiдної системи шукаємо у виглядi
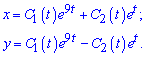(1)
Після підстановки в систему рівнянь отримаємо
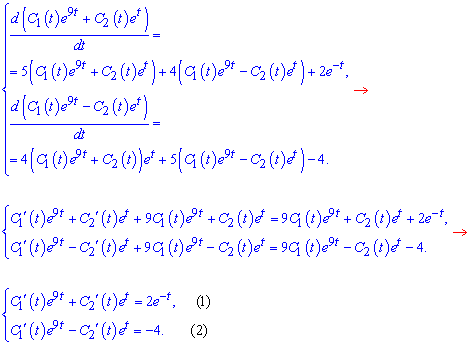
Просумуємо отримані рівняння, щоб позбутися похідної від другої сталої та інтегруванням знайти першу сталу
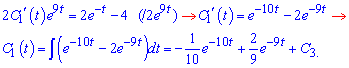
Віднявши від першого рівняння системи друге, знаходимо інтегруванням другу сталу
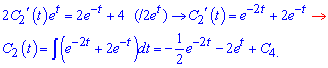
Підставивши знайденi функцiї C1(x), C2(x) у (1), одержимо загальний розв'язок заданої системи у вигляді
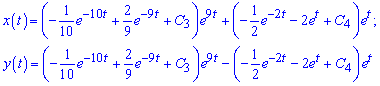
Пiсля розкриття дужок та зведення подібних доданків отримаємо
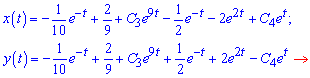
компактний вигляд розв'язку системи неоднорідних рівнянь
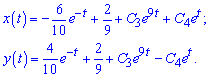
На цьому підсумкова контрольна робота з диференціальних рівнянь повністю проаналізована. Для закріплення знань знайдіть кілька подібних завдань і самостійно розв'яжіть, при потребі використовуйте наведені схеми. Це швидше допоможе вивчити методику диференціальних рівнянь.
