Завдання на практикумі з диференціальних рівнянь нічим не відрізняються від тих, що розглядаються на практичних заняттях.
Однак в аудиторії вивчають тему за темою і розглядають вузький клас завдань. На практикумі, модулі чи контрольній Вам приходиться згадувати чималий кусок теорії ДР за місяць чи симестр, і зорієнтуватися у пройденому матеріалі часом буває не просто.
Особливо гостро це питання стоїть у студентів заочної форми навчання, оскільки теорію їм начитують в досить стислі терміни, а вже розбиратися з практичною стороною, зазвичай, доводиться самостійно.
Тут підготовлено 5 завдань, на обчислення яких ми потратили не більше 20 хвилин.
Набагато більше часу пішло на оформлення відповідей у виді статтю, яку Ви зараз читаєте.
Загалом в розділі диф. р-нь нами підготовлені до основних завдань, що можуть зустрітися Вам у навчанні.
Завдання 1 Знайти загальний розв'язок лінійного однорідного диференціального рівняння (ДР)
y''''-8y''+16y=0
Розв'язок диф. р-ня четвертого порядку шукаємо у вигляді y=ekx.
Характеристичне рівняння матиме вигляд
k^4-8^2+16=0
Це біквадратне рівняння, тому робимо заміну z=k^2 та переходимо до квадратного
z^2-8z+16=0
Знайдемо дискримінант та корені
D=(-8)2-4·16=0
z=8/2=4 маємо два кратні корені.
Підставимо їх в попередню заміну та обчислимо k
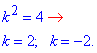
Враховуючи кратність коренів, загальний розв'язок однорідного ДР матиме вигляд
y=(C1·x+C2)e2x+(C3·x+C4)e-2x.
Завдання 2 Знайти частинний розв'язок лінійного ДР другого порядку зі сталими коефіцієнтами, що задовільняє задані умови
y''+25y=0, y(0)=1, y'(0)=6.
Розв'язок: Загальний р-зок лінійного диференціального рівняння
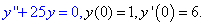
шукаємо у вигляді y=ekx.
Підставляємо у та складаємо характеристичне рівняння
k^2+25=0;
k^2=-25;
k=5i;
k=-5i.
Маємо комплексно спряжені корені, тому розв'язок матиме вигляд розкладу
y=C1cos(5x)+C2sin(5x)
Задовільнимо умову Коші та знайдемо сталі С1, С2
y(0)=C1=1;
C1=1.
y'(0)=5C2=6;
C2=6/5.
Таким чином розв'язок задачі Коші вигляд
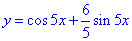
Завдання 3 Знайти частинний розв'язок лінійного диференціального рівняння другого порядку зі сталими коефіцієнтами, що задовільняє задані умови
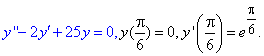
Розв'язок: Заданому однорідному ДР відповідає наступне характеристичне р-ня
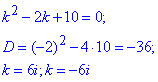
Корені характеристичного рівняння уявні комплексні числа
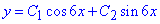
Задовільнимо умову Коші та знайдемо сталі С1, С2 з системи лінійних рівнянь
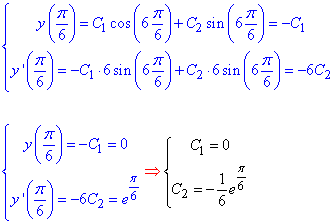
Розв'язок задачі Коші однорідного диференціаьного рівняння має вигляд
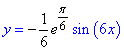
От і всі пояснення до цього завдання.
Завдання 4 Методом невизначених коефіцієнтів знайти загальний розв'язок лінійного неоднорідного диференціального рівняння (ДР) другого порядку зі сталими коефіцієнтами
2y''-3y'-5y=exp(-x)
Розв'язування: Оскільки ДР неоднорідне, то розв'язок шукаємо у вигляді суми р-ку однорідного ДР та чатинного р-ку неоднорідного ДР
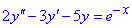
Знайдемо розв'язок однорідного диференціального рівняння (ДР)
2y''-3y'-5y=0
Його шукаємо у вигляді y=ekx.
При підстановці та спрощенні на експоненту отримаємо характеристичне рівняння
2k^2-3k-5=0
Обчислимо корені квадратного рівняння через дискримінант
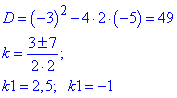
Розв'язок однорідного рівняння має вигляд
y=C1e2,5x+C2e-x.
Знайдемо частинний розв'язок неоднорідного рівняння.
Враховуючи, що степінь (-1) є коренем характеристичного рівняння, частинний р-зок ДР шукаємо у вигляді
y=Axe-x.
Знайдемо першу та другі похідні функції
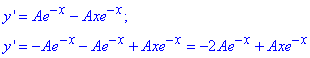
Для визначення сталої А функцію та її похідні підставляємо в диф. рівняння
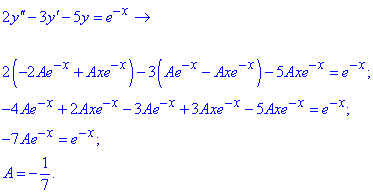
Загальний розв'язок ДР є сумою розв'язку однорідного та частинного р-ку неоднорідного ДР
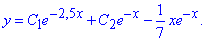
Завдання 5 Методом невизначених коефіцієнтів знайти загальний розв'язок лінійного неоднорідного різницевого рівняння другого порядку зі сталими коефіцієнтами
2yn+2-3yn+1+5yn=3n.
Розв'язування: Складаємо мультиплікаторне рівняння та розв'язуємо його 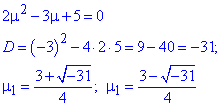
Маємо ірраціональні корені.
Розв'язок однорідного різницевого р-ня має вигляд
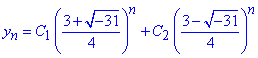
Оскільки права сторона рівна 3n, то частинний розв'зок неоднорідного різницевого рівняння шукаємо у вигляді yn=An+B.
Підставимо запис в початкове різницеве рівняння та визначимо сталі 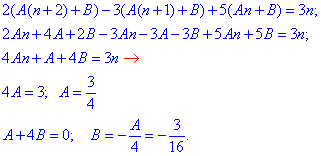
Запишемо частинний р-зок неоднорідного різницевого р-ня
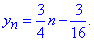
Загальний р-зок неоднорідного різницевого р-ня рівний сумі знайдених 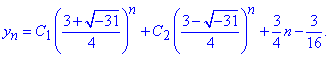
На цьому детальний аналіз відповідей заданого практикуму з ДР завершено.
На сайті опубліковано понад 200 готових розв'язків з ДР, які охоплюють практично всі теми, що розглядаються у ВУЗах з поглибленим вивченням математики.
Тож переглядайте відповіді, діліться посиланнями на кращі матеріали з рузями та обирайте для себе легкі методики обчислень.


