Студенты ВУЗ-ов частенько ищут информацию "Как найти решение уравнения в полных дифференциалах?". Из этого урока Вы получите полную инструкцию плюс готовые решения. Сначала краткое ознакомление - что такое уравнение в полных дифференциалах? Как искать решение уравнения на полный дифференциал?
Далее разбор готовых примеров, после которого возможно у Вас не останется вопросов по данной теме.
Уравнение в полных дифференциалах
Определение 1. Уравнение вида M(x,y)dx+N(x,y)dx=0 называется уравнением в полных дифференциалах, если зависимость перед знаком равенства является полным дифференциалом некоторой функции двух переменных u(x,y), то есть справедливая формула
du(x,y)=M(x,y)dx+N(x,y)dx. (1)
Таким образом, первоначальное уравнение по содержанию означает равенство нулю полного дифференциала функции
du(x,y)=0.
Интегрируя дифференциал получим общий интеграл ДУ в виде
u(x,y)=С. (2)
При вычислениях, как правило, постоянную возлагают равной нулю.
Пред вычислениями всегда возникает вопрос "Как проверить что заданное ДУ является уравнением в полных дифференциалах?"
На этот вопрос дает ответ следующее условие.
Необходимое и достаточное условие полного дифференциала
Необходимым и достаточным условием полного дифференциала является равенство между собой частных производных
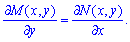(3)
При решении дифференциальных уравнений его проверяют в первую очередь, чтобы идентифицировать имеем ли уравнение в полных дифференциалах или возможно другое.
По содержанию это условие означает что смешанные производные функции равны между собой.
В формулах учитывая зависимости
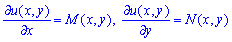(4)
необходимое и достаточное условие существования полного дифференциала можем записать в виде
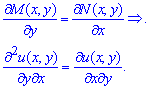
Приведенный критерий и применяют при проверке уравнения на соответствие полному дифференциалу, хотя при изучении данной темы преподаватели не зададут Вам другого типа уравнений.
Алгоритм решения уравнения в полных дифференциалах
С обозначений (4) частных производных полного дифференциала функции следует, что u(x,y) мы можем найти интегрированием
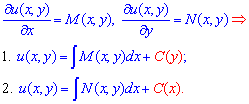
Эти формулы дают выбор при вычислениях, поэтому для интегрирования выбирают ту частную производную, интеграл от которой легче найти на практике.
Далее второй важный момент - неопределенный интеграл представляет собой первообразную то есть "+ С", которую следует определить.
Поэтому, если интегрируем частную производную M(x,y) по "икс" то сталая зависит от y и наоборот - если интегрируем N(x,y) по y то сталая зависима от "икс".
Далее чтобы определить постоянную берут производную от u(x,y ) по другой переменной чем та, по которой производили интегрирование и приравнивают к второй частичной производной.
В формулах это будет выглядеть следующим образом
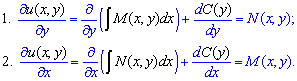
Как правило некоторые слагаемые упрощаются и получим уравнение на производную постоянной. Для первого из уравнений получим
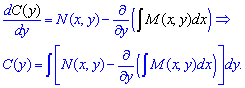
Окончательно общий интеграл после определения постоянной имеет вид
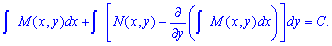
В симметричной форме получим ответ и для другого уравнения.
Запись только на вид сложная, на самом деле на практике все выглядит значительно проще и понятнее. Проанализируйте следующие задачи на полные дифференциалы.
Готовые ответы на уравнение в полных дифференциалах
Пример 1. Решить дифференциальное уравнение
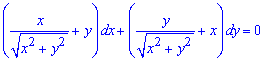
Решение:Левая часть уравнения является полным дифференциалом некоторой функции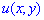 
, поскольку выполняется условие
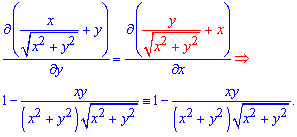
Отсюда записываем частную производную функции двух переменных от "икс"
и интегрированием находим ее вид
Чтобы доопределить постоянную находим частную производную функции по "y" и приравниваем со значением в уравнении
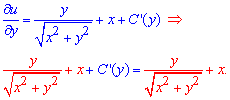
Подобные слагаемые в правой и левой части сокращаем, после чего постоянную находим интегрированием
Теперь имеем все величины для записи общего решения дифференциального уравнения в виде
Как можно убедиться, схема решения уравнений в полных дифференциалах не сложная и ее под силу выучить каждому. Важное значение имеют множители при дифференциалах, поскольку их приходится интегрировать и дифференцировать чтобы найти решение.
Пример 2. (6.18) Найти интеграл дифференциального уравнения
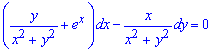
Решение: По теории левая часть уравнения должна быть полным дифференциалом некоторой функции двух переменных u(x,y), при этом проверяем выполняется ли условие
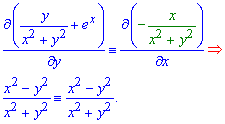
Отсюда берем частную производную и через интеграл находим функцию
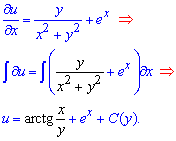
Вычисляем частную производную функции двух переменных по y и приравниваем к правой стороне дифференциального уравнения.
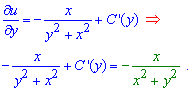
Производная выражается зависимостью
С учетом постоянной получили общий интеграл дифференциального уравнения в виде
На этом вычисления данного примера завершено.
Пример 3. (6.20) Решить дифференциальное уравнение
Решение: Левая часть уравнения будет полным дифференциалом некоторой функции двух переменных u(x; y) , если будет выполняться условие
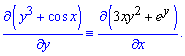
Отсюда начинаем решать уравнения, а вернее интегрирование одной из частных производных
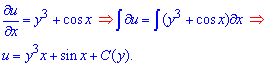
Далее находим производную от полученной функции по переменной y и приравниваем к правой стороне дифференциальной зависимости
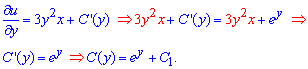
Это позволяет найти константу, как функцию от y. Если начинать раскрывать дифференциальную зависимость с правой стороны, то получим что константа зависит от x. Общее решение дифференциального уравнения при этом не изменится и для заданного уравнения имеет вид
На этом пример решен.
Пример 4. (6.21) Решить дифференциальное уравнение
Решение: Проверяем является ли полным дифференциалом некоторой функции u(x,y) выражение в левой стороне уравнения
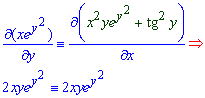
Выписываем частную производную функции двух переменных и интегрированием восстанавливаем решение
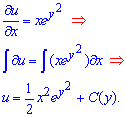
Далее уточняем постоянную. Для этого вычисляем производную функции по y и приравниваем к значению в уравнении (выделено зеленым)
Отсюда, выражаем производную и интегрируем
Общее решение дифференциального уравнения можем записать формулой
Для закрепления тематики просим самостоятельно проверить что данные уравнения являются уравнениями в полных дифференциалах и решить их:
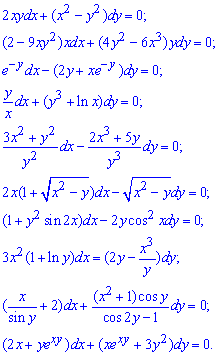Здесь Вам и корневые функции, тригонометрические, экспоненты, логарифмы, одним словом - все что может ожидать Вас на модулях и экзаменах.
После этого Вам станет гораздо проще решать такого типа уравнения.
Из следующей статьи Вы познакомитесь с уравнениями вида
M(x,y)dx+N(x,y)dx=0
которые достаточно подобные уравнению в полных дифференциалах, однако в них не выполняется условие равенства частных производных. Их вычисляют поиском интегрирующего множителя, умножая на который приведенное уравнение становится уравнением в полных дифференциалах.
