Багато студентів шукають зрозумілі пояснення та приклади, що дають відповідь на питання "Що таке мінор? Що таке алгебраїчне доповнення? Яка між ними різниця".
Про все це ви дізнаєтеся, дочитавши дану статтю до кінця, і якщо вмієте обчислювати визначники, то з прикладами на мінори та алгебраїчні доповнення труднощів у Вас не буде. Для початку основні означення, щоб всі хто знайомиться з темою знали про що йде мова.
Мінором M[j,k] визначника є визначник, одержаний з даного викреслюванням рядка та стовпця, які стоять на перетині до елемента a[j,k].
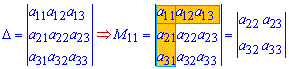
Мінори є визначниками на одиницю меншого порядку ніж матриця для якої їх шукають.
Визначник n порядку має кількість n* n мінорів (рівно кількості елементів матриці).
Для матриці 2*2 мінорами будуть протилежні елементи по діагоналі
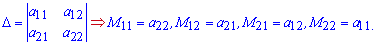
Алгебраїчне доповнення А[j,k] – це мінор M[j,k], взятий зі знаком "плюс" , якщо j+k – парне число і зі знаком "мінус" – якщо непарне
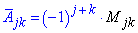
Матриця алгебраїчнихбдоповнень - це матрия складена з визначників А[j,k],j,k=1..n.
Знаки мінорів спрощено можна подати у вигляді схем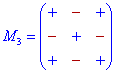
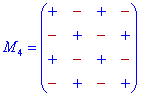
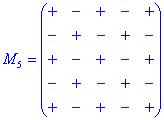 Визначник будь-якого порядку n, згідно правила Лапласа, можна записати у вигляді суми по парних добутків елементів рядків (стовпців) на їх алгебраїчні доповнення.
Визначник будь-якого порядку n, згідно правила Лапласа, можна записати у вигляді суми по парних добутків елементів рядків (стовпців) на їх алгебраїчні доповнення.
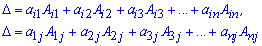
Алгебраїчне доповнення А[j,k], як і мінор, це визначник на одиницю меншого порядку ніж головний визначник. Тому для обчислення визначника n порядку потрібно обчислити n визначників n-1 порядку.
На практиці визначники матриць через алгебраїчні доповнення розписують до тих пір, поки не отримають мінори 3 порядку, які знаходять за правилом Саррюса або трикутників.
Практична реалізація для матриць більших 4 порядку складна, але реалізація таких алгоритмів на мові програмування через рекурентні формули значно спрощує обчислення.
В навчанні переважно оперують з матрицями максимум 4,5 порядку. Якщо маємо розріджені матриці (багато елементів нульових) то визначник за рядком (стовпцем), який містить найбільшу кількість нульових елементів k зводиться до знаходження кількох (n-k) визначників на 1 меншого порядку від основного. Тому з допомогою елементарних перетворень спочатку перетворюють визначник, щоб отримати найбільше нульових елементів, а вже потім розписують його через алгебраїчні доповнення. Щоб Вас не навантажувати зайвою теорією перейдемо до практичної реалізації.
Приклад 1. Знайти мінори матриці 2*2
1)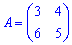
Розв'язок. Матриця мінорів за правилами матиме вигляд
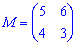
2)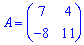
Розв'язок. Міняємо місцями елементи та записуємо у матрицю мінорів
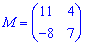
Приклад 2. Знайти мінори матриці 3*3
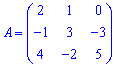
Розв'язок. Викреслюємо перший рядок і стовпець для отримання мінора до першого елемента матриці
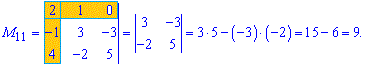
За такою схемою знаходимо усі мінори
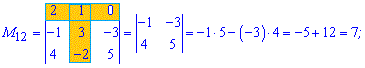
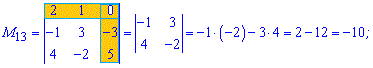
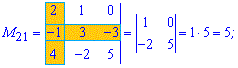
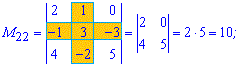
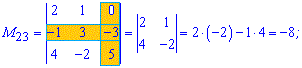
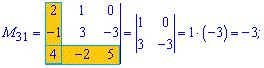
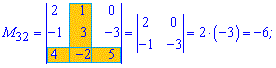
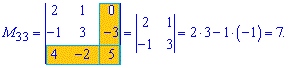
Отримані значення записуємо в матрицю мінорів
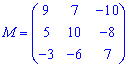
Думаю, після таких детальних пояснень Ви точно зможете знайти мінори самостійно.
Приклад 3. Знайти алгебраїчні доповнення матриці 3*3
1) 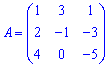
Розв'язок. За наведеною вгорі схемою обчислюємо алгебраїчні доповнення, для цього знаходимо мінори з відповідними знаками
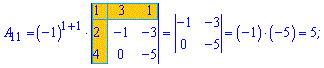
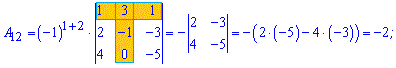
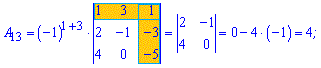
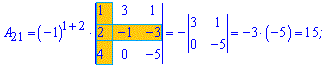
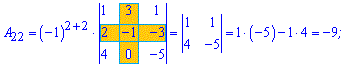
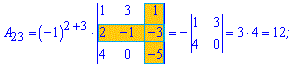
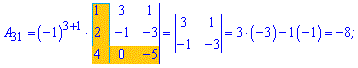
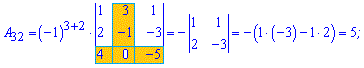
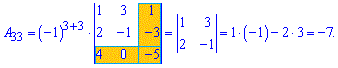
Думаю, що тепер Ви точно знаєте як знайти алгебраїчні доповнення.
Знайдені алгебраїчні доповнення записуємо у вигляді матриці
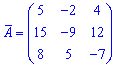
Також, для простоти обчислень, можете спочатку обчислювати мінори, а далі записувати їх у матрицю алгебраїчних доповнень з відповідними знаками. Вибирайте для себе зрозуміліший і простіший спосіб.
Приклад 4. Знайти визначник матриці 3*3
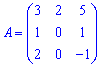
Розв'язок. Знайдемо визначник за правилом трикутника
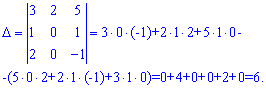
Як бачите багато добутків рівні нулю, оскільки присутні елементи. Тепер, для порівняння, за правилом Лапласа розкладемо визначник через алгебраїчні доповнення другого стовпця
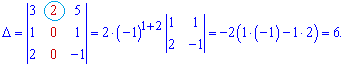
Легко переконатися, що обчислень менше, тільки потрібен час та практика, щоб звикнути до такої схеми обчислень.
Приклад 5. Знайти визначник матриці 4*4
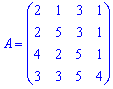
Розв'язок. На перший погляд нас чекає обчислення чотирьох мінорів третього порядку. Але насправді дану кількість можна спростити! Уважно погляньте на перший і другий рядок – вони відрізняються одним елементом. Виконаємо над визначником 4 порядку елементарне перетворення, а саме, від другого рядка віднімемо перший.
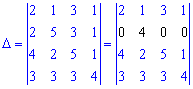
Знак визначника при цьому не поміняється. Тепер розкладемо визначник за елементами 2 рядка. Ми отримаємо 1 доданок у розкладі
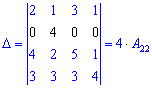
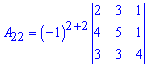
Обчислення вже спростилися. Давайте далі від другого рядка віднімемо перший щоб зробити нулем одиницю
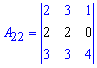
або від третього віднімемо перший, щоб позбутися 3.
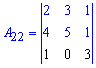
Тоді мінор 3 порядку можна, як визначник, розписати через алгебраїчні доповнення до другого або третього рядка. Обчислимо останній визначник
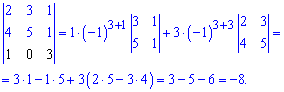
Підставимо знайдене значення у головний визначник
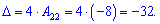
Таким чином завдяки правилу Лапласа та елементарним перетворенням нам вдалося звести відшукання визначника 4 порядку до обчислення 2 визначників 2 порядку. На практиці такі дії економлять багато часу, а в умовах контрольної чи тесту це має вирішальне значення. Тому добре розберіть наведені формули обчислень визначників та алгебраїчних доповнень та застосовуйте їх на практиці.
Вас може зацікавити:


