На попередніх заняттях проаналізовано всеможливі дробові нерівності, які можуть чекати Вас на ЗНО тестуванні.
Далі наведемо пояснення до 5 прикладів підвищеної складності.
Для школярів 10-11 класів шкіл наведені завдання можна охарактеризувати "з категорії складності (**)", однак випускники, що готуються до вступних іспитів повинні вміти вирішувати такі завдання.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 11. Дробові раціональні нерівності
Приклад 11.30 Розв'язати нерівність (x-5)/(x+5)<x.
У відповідь записати найменший цілий розв'язок.
Обчислення: Алгоритм перетворень полягає в отриманні дробу з однієї сторони, та нуля з іншої.
Оскільки умова ускладнюється, то й перетворень, що наведені у формулах дещо більше
(*)
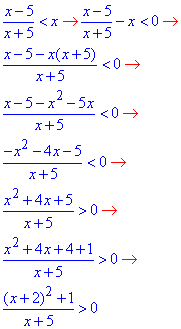Вираз (x+2)^2+1>0 більший нуля для будь-яких x, тому залежність (*) рівносильна нерівності
x+5>0, звідси x>-5.
Будуємо числову вісь та заштриховуємо потрібні значення
Множиною розв'язків є інтервал x∈(-5;+∞).
Звідси слідує, що число -4 є найменшим цілим розв'язком нерівності.
Відповідь: -4.
Незважаючи, що завдання належить до складних на попередніх уроках розглядали умови на нерівності з параметром та модулями, які в плані обчислень більш громіздкі та складні для розуміння.
Приклад 11.31 Розв'язати нерівність 2/(x+9)<x/(x-6).
У відповідь записати суму всіх цілих чисел, які не є розв'язками нерівності. Обчислення: Перетворюємо дробову нерівність до класичного вигляду
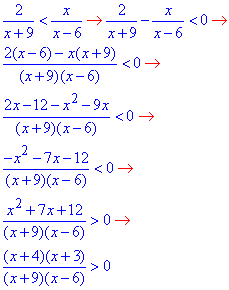
Строгу нерівність замінюємо рівносильною:
(x+4)(x+3)(x+9)(x-6)>0.
Розв'яжемо відповідне рівняння:
(x+4)(x+3)(x+9)(x-6)=0, звідси x1=-9, x2=-4, x3=-3 і x4=6.
Виколюємо знайдені точки з числової осі. В нулі функція від'ємна, далі знаки чергуються.
Множиною розв'язків нерівності є три інтервали
x∈(-∞;-9)∪(-4;-3]∪(6;+∞).
Запишемо суму всіх цілих чисел, які не задовільняють нерівність
(позначені на числовій прямій):
-9+(-8)+(-7)+(-6)+(-4)+(-3)+(-2)+(-1)+0+1+2+3+4+5+6=-24.
Відповідь: -24.
Приклад 11.32 Розв'язати нерівність 1/(1-x)≥1-2x.
У відповідь записати суму всіх додатних цілих чисел, які не є розв'язками нерівності.
Обчислення: Завдання вимагає наступних обчислень
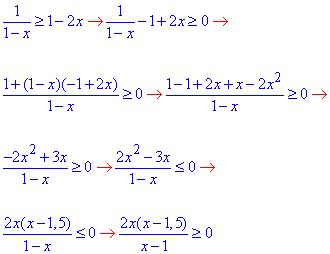
Ці формули не кінцеві, оскільки дробову нерівність можна замінити рівносильною:
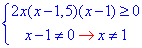
Знайдемо корені рівняння:
2x(x-1,5)(x-1)=0.
звідси x1=0, x2=1 і x3=1,5
Наносимо їх на числову вісь та визначаємо інтервали знакододатності.
Умові відповідають інтервали x∈[0;1)∪[1,5;+∞).
Єдине додатне ціле число, яке не є розв'язком заданої нерівності це 1, тому і сума дорівнюватиме 1.
Відповідь: 1.
Приклад 11.33 Розв'язати нерівність
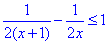
У відповідь записати суму всіх цілих чисел, які не є розв'язками нерівності. Обчислення: Перетворимо нерівність до правильного запису
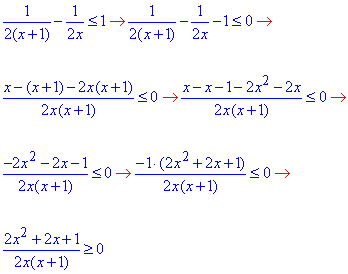
Далі нестрогу нерівність замінюємо еквівалентною системі: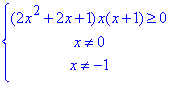 
Розв'яжемо квадратне рівняння:
2x^+2x+1=0,
D=4-4•2•1=4-8=-4<0
Робимо висновок, що рівняння розв'язку не має, далі переконуємося що квадратична форма додатна
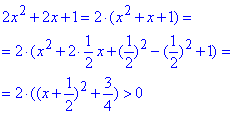
для будь-яких "ікс", тому останню систему повторно замінюємо рівносильною нерівністю:
x(x+1)>0,
Маємо 2 корені відповідного квадратного рівняння:
x1=-1 і x2=0.
Функція f=x(x+1) описує параболу з вітками вгору, тому вона додатна за межами знайдених точок.
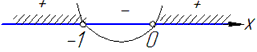
Коренями є два інтервали x∈(-∞;-1)∪(0;+∞).
Цілі числа, які не є розв'язками нерівності – це -1 і 0.
Їх сума дорівнює -1.
Відповідь: -1.
Приклад 11.34 Розв'язати нерівність 1/(x^2-3x+2) ≤1/2.
У відповідь записати добуток усіх цілих чисел, які не є розв'язками нерівності.
Обчислення:Перетворимо дробову нерівність
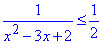
до єдиного дробу
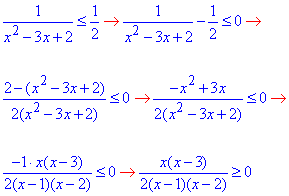
Нестрогу нерівність, що отримали, спрощуємо замінивши еквівалентною системою:
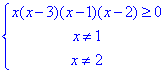
Нулями рівняння x(x-3)(x-1)(x-2)=0 є точки x1=0, x2=1, x3=2 і x4=3.
Точки наносимо на числову вісь та підстановкою будь-якої точки, яка є простою в плані обчислень, визначаємо знак на одному з інтервалів.
Далі методом "змійки" малюємо знаки на сусідніх.
Отримали 3 інтервали, що задовільняють нерівність
x∈(-∞;0]∪(1;2)∪[3;+∞).
Цілі числа, які не є розв'язками – це 1 і 2.
Обчислимо їх добуток: 1•2=2.
Відповідь: 2.
Приклад 11.35 Розв'язати нерівність
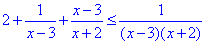
У відповідь записати найбільший цілий розв'язок.
Обчислення:Останнє завдання найважче, оскільки тут потрібно звести 4 значення до спільного дробу. Обчислення записуємо формулою
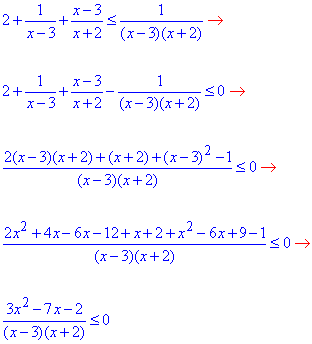
Кінцеву нерівність замінюємо рівносильною системою:
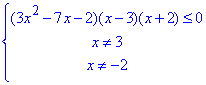
Розв'яжемо квадратне рівняння через дискримінант:
3x^2-7x-2=0;
D=(-7)^2-4•3•(-2)=49+24=73;
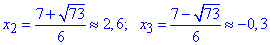
Крім цього маємо ще дві точки:
(3x^2-7x-2)(x-3)(x+2)=0, звідси
x1=-2, 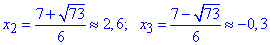і x4=3.
4 точки розбивають числову вісь на 5 інтервалів, знаки на яких наведені на рисунку
Множиною розв'язків є інтервали
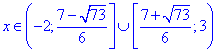
З цілих чисел тільки -1 належить інтервалам.
Відповідь: -1.
На цьому всі завдання, які рекомендовані для підготовки до ЗНО тестів з математики обчислені.
Усі важливі моменти детально розжовані та зроблено акцент на завданнях, які можна трактувати двояко.
Показано де студенти та школярі найчастіше допускають помилки.
Вам залишається перевірити весь арсенал прийомів на подібних завданнях самостійно та переконатися, що Ви готові до будь-яких перевірок.
