підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Логарифмічну нерівність розв'язують застосуванням всіх можливих властивостей логарифма, при цьому потрібно пам'ятати про область визначення логарифма.
Приклад 94. Розв'яжіть нерівність:
1) 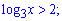
Розв'язання.
Перетворимо логарифмічну нерівність
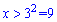
Область визначення логарифма накладає обмеження у вигляді x>0, що не суперечить знайденому. Отже, нерівність виконується при x>9.
2) 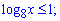
Розв'язання.
Використовуємо схему попереднього прикладу. Область визначення буде такою самою x>0.
Логарифмічну нерівність зводимо до наступної 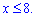
В парі з ОДЗ це дає такий розв'язок нерівності
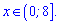
3) 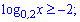
Розв'язання.
Область визначення – додатна вісь абсцис. Перший приклад з основою меншою одиниці. Запам'ятайте, в таких випадках знак при розкритті змінюється на протилежний
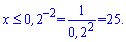
Разом з верхньою умовою отримаємо наступний розв'язок
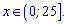
4) 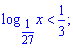
Розв'язання.
Завдання аналогічне попередньому - з усіх можливих обмежень встановлюємо розв'язок
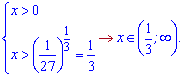
Просто і зрозуміло.
5) 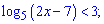
Розв'язання.
Під логарифмом міститься функція - вона повинна бути додатною
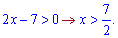
Розв'язок логарифмічної нерівності після спрощень
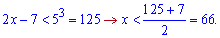
буде наступним
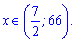
6) 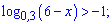
Розв'язання.
Змінюємо знак при розкритті логарифма, оскільки основа менша одиниці
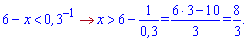
Крім того маємо умову на логарифм
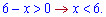
Остаточно отримаємо такий розв'язок логарифмічної нерівності
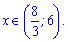
7) 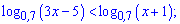
Розв'язання.
Областю визначення буде множина точок
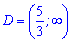
Основа менша одиниці – потрібно змінити знак при розкритті логарифмічної нерівності.
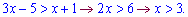
Таким чином розв'язком буде інтервал
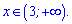
8) 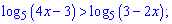
Розв'язання.
Область визначення дає обмеження на змінну з двох сторін
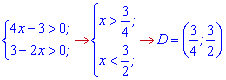
Розкриваємо нерівність

Отримали малий інтервал на якому виконується нерівність
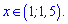
Інші приклади можете переглянути за посиланням нижче.
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Логарифмічні рівняння. №92, 93
- Наступні відповіді - Логарифмічні нерівності. №94
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



