підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) відповіді: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 4. Для кожної з функцій, графік якої зображено на рисунку 1, установіть:
1) чи визначена ця функція в точці x0 ;
2) чи існує границя функції в точці x0 ;
3) якщо границя в точці x0 існує, то чи дорівнює вона значенню функції в цій точці.
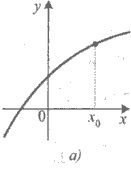
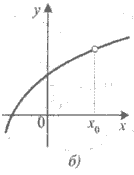
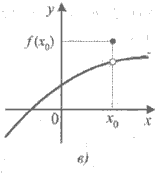
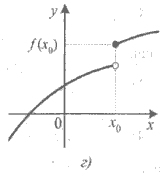
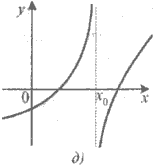
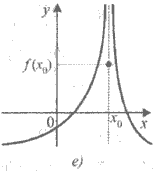
Рис.1. Графіки функцій.
Розв'язання:
За озхначенням функція визначена в точці, якщо вона існує і неперервна в деякому її околі (навколо точки). Границя існує в точці - рівносильне тому, що функція в точці приймає скінченне значення (обмежена). Останнє твердження слід перевіряти співвставленням границь
1) а);
2) а); б); в); г);
3) а) так; б) так; в) і г) ні.
Приклад 5. Користуючись означенням границі функції, доведіть, що:
Границі підібрано так, що не потрібно нічого спрощувати. Виконуємо безпосередню підстановку значення
1)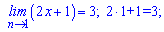
2 )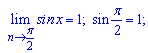
Приклад 6. Обчисліть границю функції:
1) Границю знаходимо підстановкою
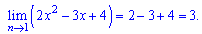
2) Маємо випадок, коли при підстановці точки отримаємо невизначеність типу 0/0.
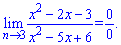
В таких випадках необхідно розкласти чисельник і знаменник на множники.
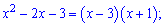
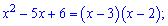
Далі виконаємо підстановку в границю та спрощення
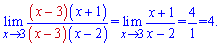
3) Границі, які в знаменнику мають корені розкривають методом домноження на спряжене до знаменника, щоб позбутися ірраціональності. В результаті складну границю можна швидко знайти
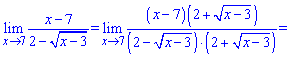
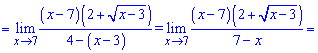
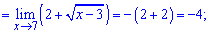
4) Зводимо до спільного знаменника та спрощуємо границю
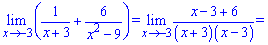
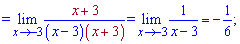
5) Перетворюємо знаменник, щоб звести до чудової границі
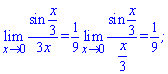
6) Границя першої функції рівна нулеві, друга функція по модулю може приймати максимум одиницю. На основі цього знаходимо границюі
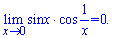
Приклад 7. Доведіть, що функція f неперервна в точці x0:
1) f(x)=3*x-1, x0=2;
Розв'язання:
Функція f(x)=3*x-1 це пряма, областю визначення є всі дійсні числа, тому функція неперервна всюди, а отже і в точці х0=2. Також можемо використати означення границі
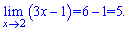
Границя існує, отже функція неперервна.
2) f(x)=x2-4 if x f(x)=3x if x>=4, x0=4.
Розв'язання:
Задана функція
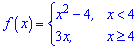
неперервна на кожному із заданих проміжків 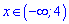 та
та 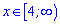 .
.
Проте в точці х0=4 потрібно знайти односторонні границі справа та зліва Обчислимо їх
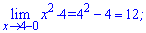
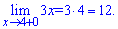
Переконуємося, що границі рівні - отже функція неперервна в точці х0=4.
Приклад 8. Доведіть, що функція f(х) не є неперервною в точці х0=1.
f(x)=x^2 if x<>1 and
f(x)=-1 if x=1, x0=4.
Розв'язання:
Функція визначена на всій дійсній осі. В точці х=1 вона не є неперервною, тому що границі справа та зліва рівні 1,
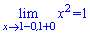
а саме значення функції в цій точці рівне мінус одиниці.
Отже функція має розрив першого роду.
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Границя числової послідовності
- Наступні відповіді - Приріст функції. Поняття похідної
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал -порекомендуйте друзям!



