Уважаемые школьники, выпускники, абитуриенты, этот раздел поможет подготовиться к внешнему независимому оцениванию по математике в 2015 года. Ответы к тестам помогут Вам понять материал и методику вычислений, систематизировать и повысить накопленный уровень знаний по математике.
Раздел II. Уравнения и неравенства
Задача 2.1 -2.36 имеют по пять вариантов ответов, из которых только один правильный. Правильно выполненное задание оценивается 1 баллом.
Задача 2.1 Решите систему уравнений
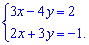
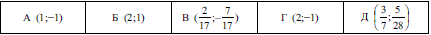Решение: Имеем систему линейных уравнений с двумя неизвестными. Умножим первое уравнение на три, а второе на четыре и найдем их сумму.
В результате получим
(9+8)*х=6-4=2;
х=2/17.
Подставим найденное решение во второе уравнение
3*y=-1-4/17=-21/17;
y=-21/(3*17)=-7/17.
Решением системы уравнений является пара чисел
(2/17; -7/17),
что соответствует варианту В тестов ВНО по математике.
Ответ: В.
Задача 2.2 Решите уравнение
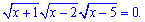
Решение: Есть достаточно простое с одной стороны иррациональное уравнение. Решение каждого из корней имеет значение
х=-1; х=2; х=5.
Многие при тестировании поспешат и впишут в ответ вариант В тестов, однако это неправильный ответ.
В подобных задачах следует проверять область допустимых значений (ОДЗ).
Согласно правилам, подкорневая функция должна быть неотъемлемой
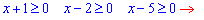
Общей для корней ОДЗ будет при переменной не менее 5.
Итак х=5 – единственный корень уравнения.
Отсюда ответом будет вариант Д, а не В, как предполагалось ранее.
Ответ: Д.
Задача 2.3 Найдите произведение корней уравнения
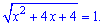
Решение: Выполним некоторые преобразования над корнем. Для начала запишем его в виде полного квадрата
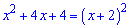
Если извлечь корень из выражения то получим модуль функции
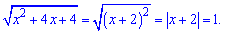
Находим точку, в которой подмодульная функция меняет знак
x+2=0 х=-2.
При переменной x>-2 раскрываем модуль и находим корень уравнения
х+2=1; x=1-2=-1.
Он принадлежит интервалу на котором искали корень, следовательно является решением.
При меньших значениях переменной х <-2 подмодульная функция при раскрытии модуля меняет знак на противоположный.
Поэтому уравнение имеет вид
-x-2=1; x=-2-1=-3.
По условию задачи вычисляем произведение корней
(-1)*(-3)=3.
Вот и вся математика.
Ответ: Д.
Оставайтесь с нами и подготовка к ВНО 2015 по математике останется для Вас приятным воспоминанием и сэкономит много времени и денег на репетиторов.
