Уважаемые школьники, выпускники, абитуриенты, этот раздел поможет подготовиться к экзаменам, тестам, внешнему независимому тестированию по математике в 2015 году. Ответы к тестам помогут Вам понять материал и методику вычислений, систематизировать и повысить накопленный уровень знаний по математике. Решение примеров будут интересны для школьников 9, 10, 11 классов, а так же их родителей.
Раздел II. Уравнения и неравенства
Задача 2.1 -2.36 имеют по пять вариантов ответов, из которых только один правильный. Правильно выполненное задание оценивается 1 баллом.
Задача 2.7 (Т-07, 29) Укажите сколько действительных корней имеет уравнение х^3 - 4|х| = 0.
Решение: Схема вычислений заключается в следующем - раскрываем модуль и находим корни, принадлежащие интервалам
x>0; x^3-4x=0;
x=0; x=-2; x=2.
x<0; x^3+4x=0;
x(x^2+2)=0; x=0.
Получили два корня x=2; x=0, что соответствует варианту В ВНО тестов.
Ответ: В.
Задача 2.8 Корень уравнения
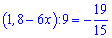
равен:
Решение: Приведем дробное уравнение к виду
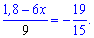
Используя пропорции выполним преобразования
1,8-6*х=-(19*9/15)=-( 19*3/5)=-(57/5)=-11,4
и найдем корень уравнения
6х=1,8+11,4=13,2;
х=13,2/6=2,2.
Из ответов к тестам подходит вариант Г.
Ответ: Г.
Задача 2.9 Решите неравенство
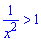
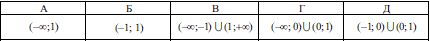Решение: Выписываем условие на область допустимых значений (x<>0). Переносим единицу за знак неравенства и сводим под общий знаменатель
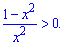
Нулями числителя являются точки x = 1; x = 1. К тому же функция парная, следовательно решение будет симметричным относительно оси Oy.
Подстановкой числа, например двойки, убеждаемся что решением являются интервалы
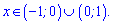
Решение неравенства соответствует варианту Д тестов.
Ответ: Д.
Оставайтесь с нами и подготовка к ВНО 2015 по математике останется для Вас приятным воспоминанием и сэкономит много времени и денег на репетиторов. Помощь по математике в виде готовых решений облегчит учебу всех школьников и будет хорошей инструкцией на экзаменах и тестах.
