На практике это все реализуется достаточно просто. Базис, как правило, проверяют на плоскости или в пространстве, а для этого нужно найти определитель матрицы второго, третьего порядка составленный из координат векторов. Ниже схематически записаны условия, при которых векторы образуют базис
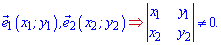
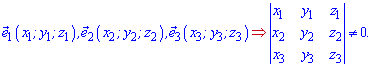
Чтобы разложить вектор b по базисным векторам
e[1],e[2]...,e[n] необходимо найти коэффициенты x[1], ..., x[n] при которых линейная комбинация векторов e[1],e[2]...,e[n] равна вектору b:
x1*e[1]+ ... + x[n]*e[n] = b.
Для этого векторное уравнение следует преобразовать к системе линейных уравнений и найти решения. Это также достаточно просто реализовать.
Найденные коэффициенты x[1], ..., x[n] называются координатами вектора b в базисе e[1],e[2]...,e[n].
Перейдем к практической стороне темы.
Разложение вектора по векторам базиса
Задача 1. Проверьте, образуют ли векторы a1, a2 базис на плоскости
1) a1 (3; 5), a2 (4; 2)
Решение: Составляем определитель из координат векторов и вычисляем его
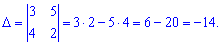
Определитель не равен нулю, следовательно векторы линейно независимы, а значит образуют базис.
2) a1 (2; -3), a2 (5;-1)
Решение: Вычисляем детерминант составленный из векторов
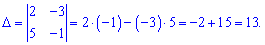
Определитель равен 13 (не равен нулю) - из этого следует что векторы a1, a2 является базисом на плоскости.
---=================---
Рассмотрим типичные примеры из программы МАУП по дисциплине "Высшая математика".
Задача 2. Показать, что векторы a1, a2, a3 образуют базис трехмерного векторного пространства, и разложить вектор b по этому базису (при решении системы линейных алгебраических уравнений использовать метод Крамера).
1) a1 (3; 1; 5), a2 (3; 2; 8), a3 (0; 1; 2), b (−3; 1; 2).
Решение: Сначала рассмотрим систему векторов a1, a2, a3 и проверим определитель матрицы А
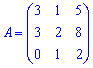
построенной на векторах отличных от нуля. Матрица содержит один нулевой элемент, поэтому детерминант целесообразнее вычислять как расписание по первому столбцу или третей строчке.
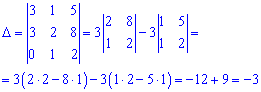
В рекзультаье вычислений получили что определитель отличен от нуля, следовательно векторы a1, a2, a3 линейно независимы.
Согласно определению векторы образуют базис в R3. Запишем расписание вектора b по базису
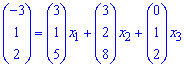
Векторы равны, когда их соответствующие координаты равны.
Поэтому из векторного уравнения получим систему линейных уравнений
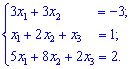
Решим СЛАУ методом Крамера . Для этого запишем систему уравнений в виде
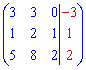
Главный определитель СЛАУ всегда равен определителю составленному из векторов базиса
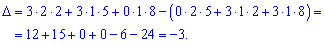
Поэтому на практике его не исчисляют дважды. Для нахождения вспомогательных определителей ставим столбец свободных членов на место каждого столбца главного определителя. Определители вычисляем по правилу треугольников
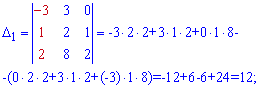
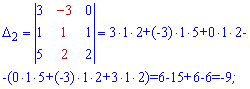
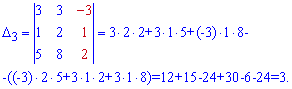
Подставим найденые определители в формулу Крамера
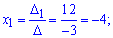
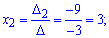
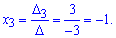
Итак, разложение вектора b по базису имеет вид b=-4a1+3a2-a3. Координатами вектора b в базисе a1, a2, a3 будут (-4,3,-1).
2) a1 (1; -5; 2), a2 (2; 3; 0), a3 (1; -1; 1), b (3; 5; 1).
Решение: Проверяем векторы на базис - составляем определитель из координат векторов и вычисляем его
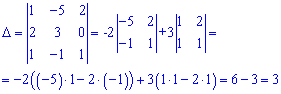
Определитель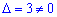 
не равен нулю, следовательно векторы образуют базис в пространстве. Осталось найти расписание вектора b через данный базис. Для этого записываем векторное уравнение
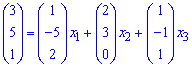
и преобразуем к системе линейных уравнений
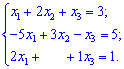
Записываем матричное уравнение
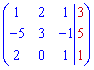
Далее для формул Крамера находим вспомогательные определители
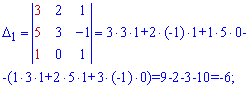
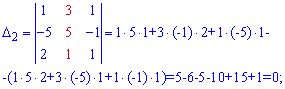
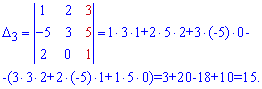
Применяем формулы Крамера
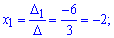
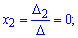
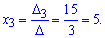
Итак заданный вектора b имеет расписание через два вектора базиса b=-2a1+5a3, а его координаты в базисе равны b(-2,0, 5).
Задача 3. Доказать что векторы a1, a2, a3 образуют базис в пространстве
1) a1 (3;-2;1), a2 (2; -5; 4) , a3 (2; -3; -1)
Решение: Записываем координаты в определитель и применяем правило треугольников для определителя
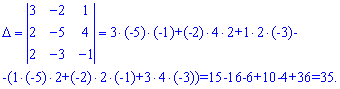
Поскольку определитель (=35) не равен нулю то векторы образуют базис в пространстве.
2) a1 (1; 1;1), a2 (2; -3; 2) , a3 (3; 4; 1)
Решение: Вычисляем определитель составленный из векторов
Det=1*(-3)*1+1*2*3+1*2*4-(1*(-3)*3+1*2*1+1*2*4)=-3+6+8+9-2-8=10 .
Векторы a1, a2, a3 линейно независимы (Det=10), а значит образуют базис в пространстве.
Теперь Вы знаете как проверить, что векторы образуют базис и сможете без проблем разложить вектор по базису.
Посмотреть материалы:
]]>Координаты вектора 
равны разнице соответствующих координат конца и начала вектора. Если 
и 
- соответственно начало и конец вектора, то
Длиной или нормой вектора 
(обозначают 
) называют неотрицательное значение квадратного корня из суммы квадратов координат вектора
Например, если 
то
.
Углом между ненулевыми векторами
и 
называется значение угла 
, которое определяется из равенства
---------------------------------------------------------------
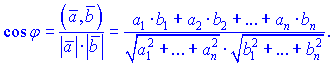
Задача 1.
Найти длину векторов 
и 
, если их начала и концы заданные вершинами
Решение.
Найдем векторы 
и 
Вычислим длину векторов
Найдем скалярное произведение векторов
Найденные значения подставляем в формулу для вычисления угла между векторами
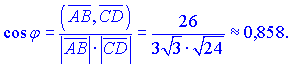
Отсюда окончательно находим значение угла 
-----------------------------------------------------
Посмотреть материалы:
]]>Пусть нам задано векторы
из 
- мерного векторного пространства, а также некоторые действительные числа
а
Вектор
называется линейной комбинацией векторов
Векторы бывают линейно зависимыми или независимыми. Эти свойства определяют на основе следующих правил:
1) Векторы 
называются линейно зависимыми, если найдутся такие действительные числа 
одновременно не равны нулю, при которых подтверждается равенство
2) Если равенство
выполняется только при условии, что
тогда векторы 
называются линейно независимыми.
На практике линейную независимость векторов проверяют из условия, что определитель составленный из координат векторов отличен от нуля. Для прибора, если есть три вектора 
из пространства, то для подтверждения их линейной независимости определитель
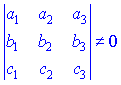
не должно быть равен нулю. В противном случае векторы будут линейно зависимыми.
Из свойств определителей следует, что векторы 
будут линейно зависимы тогда и только тогда, когда хотя бы один из них является линейной комбинацией других или нулевым.
Размерность пространства - это максимальное количество линейно независимых векторовкоторое может быть в нем. Любую совокупность линейно независимых векторов
- мерного линейного пространства 
называют его базисом.
Каждый вектор 
из 
единственным способом может быть изображен в виде линейной комбинации векторов базиса. Если
- базис линейного пространства 
, то 
- разложение вектора по базису 
,
-координаты вектора 
в этом базисе.
Задачи разложения вектора занимают важное место в курс высшей математики, и нужны не меньше отыскания базиса линейного пространства.
------------------------------------
Алгоритм разложения вектора по базису
1. Записать равенство 
в матричной форме. Векторы 
представить в виде матриц-столбцов.
2. Матричное уравнение записать в виде системы линейных алгебраических уравнений. Решить полученную систему.
3.Записать расписание вектора
по базису 
.
Для этого в равенство
вместо 
подставить решения системы уравнений.
----------------------------------
Задача 1.
Записать разложение вектора 
по базису
Решение.
Воспользуемся формулой разложения вектора
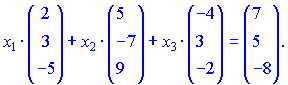
Данное уравнение записываем в виде системы линейных уравнений
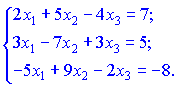
Решением этой системы 
Полученные значения подставляем в уравнение разложения, в результате получим 
- расписание вектора 
в базисе 
Как видите вычисления не сложные, приведена инструкция поможет Вам решить подобные задачи.
----------------------------------------------
Посмотреть материалы:
]]>Пусть имеем две точки 
и нужно найти точку 
на отрезке 
которая делит его в отношении
Координаты точки 
ищем по формулам
В случае разделения отрезка пополам получим известную формулу
Рассмотрим примеры.
----------------------------------
Задача 1.
Отрезок 
, соединяющий точки 
и 
разделить в отношении 
Решение.
По правилам деления отрезка находим координаты искомой точки 
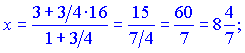
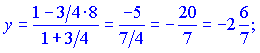
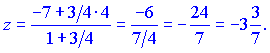
Неизвестная точка будет иметь координаты
----------------------------------
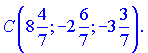
Задача 2.
Найти точку 
, которая делит отрезок 
в отношении 
, если известно координаты точки деления 
и начало отрезка 
Решение.
Подставляем наши данные в формулы деления отрезка
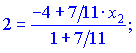
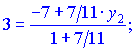
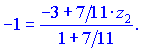
Из полученных неравенств определяем координаты конца отрезка 
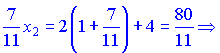
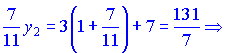
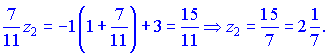
Окончательно точка 
будет иметь координаты
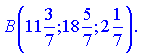
Еще ряд новых задач Вы встретите в геометрии, однако и они решаются с помощью рассмотренных формул.
----------------------------------------------
Посмотреть материалы:
]]>І. Суммой двух 
-мерных векторов
и 
называют
-мерный вектор 
, координаты которого равны сумме соответствующих координат векторов - слагаемых:
Например, если 
,
то 
Из этого правила следует, что разностью двух векторов будет вектор, координаты которого является разницей соответствующих координат векторов
ІІ. Произведением числа 
(скаляра) на 
-мерный вектор 
называется 
-мерный вектор 
, координаты которого равны произведению числа 
на соответствующие координаты вектора 
Например
Операции сложения векторов и умножения числа на вектор (
- некоторые числа) обладают свойствами:
1) 
2) 
3)
4)
5)
6)
7) Для произвольного вектора 
существует противоположный вектор 
такой, что
ІІІ. Скалярным произведением 
двух 
-мерных векторов 
и 
называют число, равное сумме произведений соответствующих координат векторов:
Например,
если
, то
Согласно другому определению, скалярное произведение двух векторов это число, равное произведению длин векторов (их модулей) на косинус угла между ними
Из приведенного выше определения можно получить формулу для вычисления угла между векторами
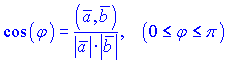
или в координатной форме
Также есть формулировка согласно которой скалярное произведение двух векторов равен модулю одного из них умноженному на проекцию второй вектор на направление первого
Из последнего определения вытекают формулы для нахождения проекции вектора на вектор
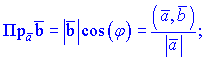
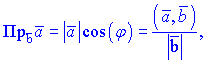
или в координатной форме
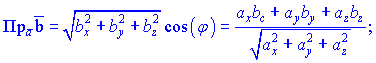
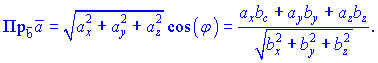
Примеры нахождения скалярного произведения, угла между векторами и проекции одного вектора на другой будут рассмотрены ниже.
Алгебраические свойства скалярного произведения векторов:
1) 
2)
3)
4)
Равенство 
имеет место при условии
Геометрические свойства скалярного произведения
1)векторы 
перпендикулярны между собой, если
2) угол между векторами 
острый в случаях, когда
3) угол между векторами 
тупой в случаях, когда
ІV. Векторным произведением 
или 
двух векторов называется вектор 
, который отвечает следующим условиям:
1) модуль вектора 
равен произведению модулей векторов 
и 
на синус угла между ними
2) вектор 
нормальный к плоскости, построенной на векторах 
и 
;
3) вектор 
направлен так, что с его конца кратчайший поворот от вектора 
к 
происходит против часовой стрелки. Иными словами, векторы 
образуют правую тройку.
Векторное произведение имеет следующие геометрические свойства:
Его модуль равен площади параллелограмма построенного на векторах 
и 
Поэтому площадь треугольника построенного на векторах 
и 
равна модулю половины векторного произведения этих векторов
Алгебраические свойства векторного произведения
1) векторное произведение 
равно нулю в случае коллинеарности векторов или когда один из них нулевой;
2) от перестановки векторов векторное произведение меняет знак на противоположный
3)
4)
На практике важно иметь под рукой формулу для вычисления векторного произведения в координатной форме, поэтому запишем и ее
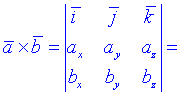
Рассмотрим конкретные примеры для усвоения пройденного материала.
--------------------------------------------
Задача 1.
Заданы векторы 
и 
Найти следующие величины
1) сумму векторов 
2) скалярное произведение векторов 
3) ) векторное произведение 
площадь треугольника построенного на векторах 
4) угол между векторами 
5) проекцию каждого из векторов на другой
Решение
1) Проведем вычисления
2) Скалярное произведение будет равно
3) Векторное произведение вычисляем по формуле
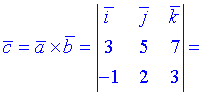
Площадь треугольника будет равна
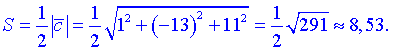
4) Найдем угол между векторами по формуле
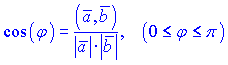
В ней скалярное произведение уже найдено поэтому находим длины векторов
Подставляем нужные значения в формулу
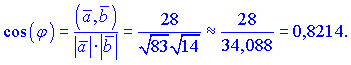
Находим значение угла
5) Найдем проекции векторов
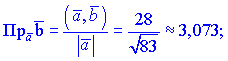
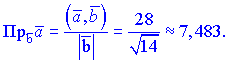
Проекции векторов можно искать через косинус угла между векторами, результат от этого не изменится
На этом урок окончен. Изучайте правила и свойства операций над векторами, они станут Вам полезны при обучении.
-----------------------------------------------------
Посмотреть материалы:
]]>
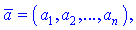
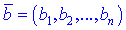
называют число равное сумме попарных произведений координат векторов с каждой оси, т.е.
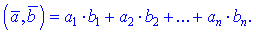
Из формулы видно что вычисление скалярного произведения - это самое простое занятие, которое может выполнить любой школьник.
Например, если есть два вектора в пространстве с координатами
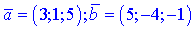
то их скалярное произведение равно 6
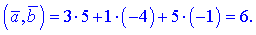
В математике есть еще одно определение скалярного произведения.
Согласно второму определению скалярное произведение двух векторов равно числу, которое получают умножением длин векторов (их модулей) на косинус угла между ними
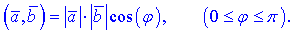
Данное определение используют не столько для нахождения скалярного произведения, как для исчисления значение косинуса угла и уже из таблиц - самого угла между векторами. Из определения получают удобную формулу для вычисления угла между векторами
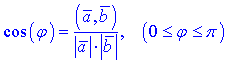
или в координатной форме
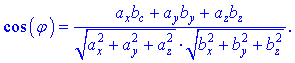
Приведем примеры вычисления скалярного произведения для трехмерных векторов.
--------------------------------------------
Примеры.
Задано векторы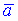 
и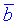 
. Вычислить их скалярное произведение, если
1) 
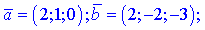
2) 
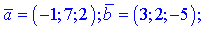
3) 
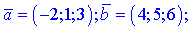
4) 
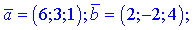
5) 
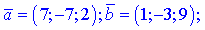
6) 
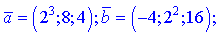
7) 
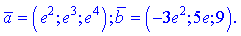
Решение. Выполним вычисления согласно формул
1) 
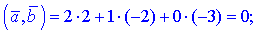
2) 
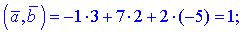
3) 
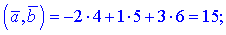
4) 
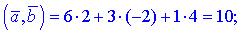
5) 
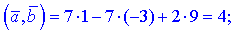
6) 
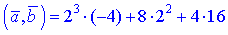
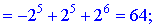
7) 
-----------------------------------
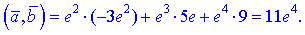
Из примеров Вы убедились, что нахождение скалярного произведения попарным перемножением координат векторов, а затем их суммированием не является сложным. В следующих статьях будут рассмотрены другие стороны скалярного произведения и его применение к векторному анализу.
Посмотреть материалы:
]]>
называется число, равное векторному произведению первых двух векторов, 
, умноженному скалярно на вектор 
. Векторами это можно представить так
Так как векторы 
на практике задают в координатной форме, то их смешанный произведение равен определитель, построенном на их координатам
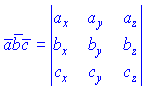
В силу того, что векторное произведение антикомутативно, а скалярное произведение коммутативно, то циклическая перестановка векторов в смешанном произведении не изменяет его значение. Перестановка двух соседних векторов меняет знак на противоположный
Смешанный произведение векторов положительный, если они образуют правую тройку и отрицательный - если левую.
Геометрические свойства смешанного произведения
1. Объем параллелепипеда, построенного на векторах 
равен модулю смешанного произведения этих векторов
2. Объем четырехугольной пирамиды равен трети модуля смешанного произведения
3. Объем треугольной пирамиды равен одной шестой модуля смешанного произведения
4. Векторы 
планарных тогда и только тогда, когда
В координатах условие компланарности означает равенство нулю определителя
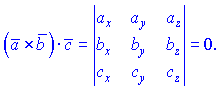
Для практического усвоения рассмотрим примеры.
-------------------------------------------
Пример 1.
Определить, какой тройкой (правой или левой) являются векторы
1)
2) 
3) 
4)
5) 
Решение.
Найдем смешанное произведение векторов и по знаку выясним, какую тройку векторов они образуют
1) 
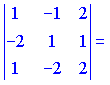
Векторы образуют правую тройку (
).
2) 
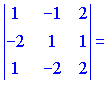
Векторы образуют правую тройку (
).
3) 
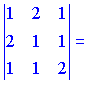
Векторы образуют левую тройку (
).
4)
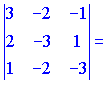
Векторы образуют правую тройку (
).
5)
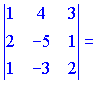
Векторы образуют левую тройку (
).
6)
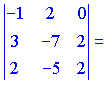
Данные векторы линейно зависимы.
-------------------------------------------
Пример 2.
Выяснить линейную зависимость векторов
1)
2)
3)
Решение.
Найдем смешанный произведение и проверим отличны от нуля определители
1) 
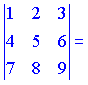
Векторы линейно зависимы (
).
2)
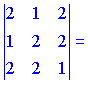
Векторы линейно независимы (
) и образуют левую тройку.
3) 
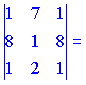
Векторы линейно зависимы (
).
Таким методом можно решить множество других задач, все в конечном итоге сводится к отысканию определителей третьего порядка. Находим определитель, анализируем его значение и принимаем нужный ответ.
----------------------------------------------
Посмотреть материалы:
]]>Тетраэдр в пространстве задано вершинами
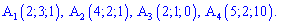
Необходимо найти:
1) уравнение грани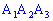 
;
2) уравнение высоты пирамиды, которая проходит через вершину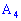 
;
3) длину этой высоты;
4) угол между ребром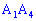 
и гранью 
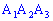в градусах;
5) площадь грани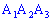
;
6) Объем пирамиды.
Решение.
1) Уравнение грани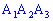 
Запишем уравнение плоскости в виде.
.
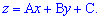Поскольку все три точки принадлежат этой плоскости, то, подставляя их по очереди получим систему уравнений
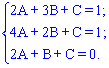
Решая ее получим.
.
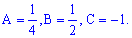Подставляя в исходное уравнение получим
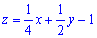, Или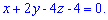 
.
2) Уравнение высоты пирамиды, проходящей через вершину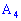 
Запишем уравнение высоты пирамиды, проходящей через вершину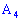
.
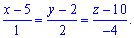3) Высота с вершины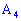 
Найдем высоту, для этого найдем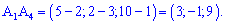 
Высоту найдем учитывая уравнение грани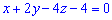 
, по формуле
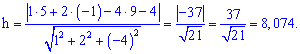
4)Угол между ребром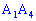 
и гранью 
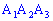в градусах
Найдем угол между ребром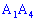 
и гранью 
(
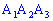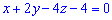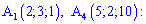
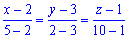) . Запишем уравнение прямой, проходящей через точки 
, или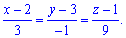 
.
Найдем синус угла по формуле
.
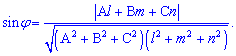Подставим значения
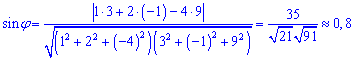
Найдем значение угла
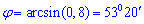
5) Площадь грани 
Площадь грани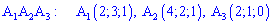
найдем по формуле
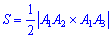
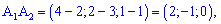
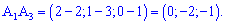
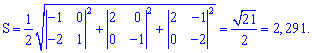
6) Объем пирамиды
Найдем объем пирамиды пирамиды по формуле
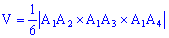, где
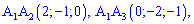
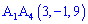
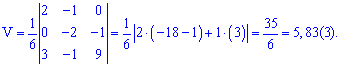
Математический калькулятор YukhymCalc решает эту задачу и немало типичных для студенческой практики математических задач. Фрагмент работы калькулятора приведены ниже.
------------------------------
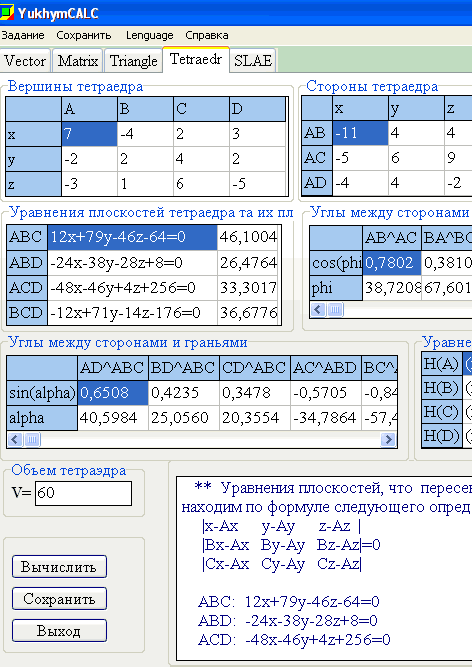
Посмотреть материалы:
]]>