Вычисление определителей второго, третьего и старших порядков можно быстро осуществить с помощью программы-калькулятора YukhymCalc. Скачать ее можно по ссылке в конце статьи, а сейчас рассмотрим как возникли определители и правила их вычисления.
-----------
Решение многих задач математики, экономики, статистики, механики, сводится к решению систем линейных алгебраических уравнений.
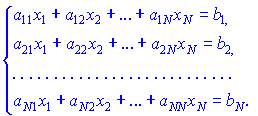
В результате вычислений получаем, что система одно решение, множество или нет ни одного. Давайте выясним от чего это зависит? Рассмотрим, для примера два линейных уравнения с двумя неизвестными:
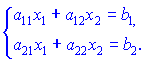
неизвестными Для решения этих уравнений мы должны умножить их на соответствующие множители, при которых исключается одно из неизвестных 
или
: первое на 
минус второй на 
для нахождения 
; второе на 
минус первое на 
для нахождения 
На основе этого
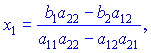
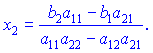
Эти выражения верны при условии, что знаменатель не равен нулю
Если
,то система уравнений или нет решения, или имеет бесконечное количество решений. Выражение в знаменателе (
), которые являются одинаковыми при двух неизвестных, называют определителем и обозначают
Определителем второго порядку называется число, равное разнице произведений элементов главной и вспомогательной диагоналей, т.е
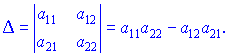
Определителем третьего порядка находят по правилу треугольников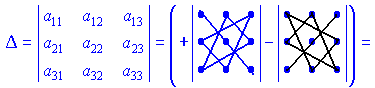 
Это правило легко запомнить, если дописать рядом с определителем первый и второй в столбце.
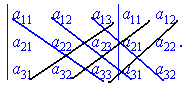
Данный метод вычисления определителя третьего порядка называется правилом Саррюса. В процессе вычислений систем линейных уравнений установлено, что определители равны сумме слагаемых, которые определяются как произведение элементов, взятых по одному одновременно с каждой строки и столбца. Для системы трех уравнений в произведение входит три элемента, четырех - четыре и т. д. Количество слагаемых в определителе в общем равна факториала числа уравнений. В случаях нулевых коэффициентов при неизвестных нахождения определителя упрощается. Для вычисления определителей старших порядков используют правила.
--------------------------------------------
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
1. Величина определителя не изменится, если его строки заменить столбцами, причем каждая строка заменяют столбиком с тем же номером (транспонирования).
2. Если в определителе поменять местами только две строки (или два столбца), то определитель меняет знак на противоположный, сохраняя свое абсолютное значение.
3. Если определитель имеет два одинаковых колонки или два одинаковых строки, то он равен нулю.
4. Если определитель содержит два пропорциональных строк (столбцов), то его значение равно нулю. Если элементы некоторого строки (столбца) равны нулю, то и сам определитель равен нулю.
5.Если все элементы некоторого строки (столбца) умножить на постоянное число, то значение определителя также умножится на это число. Отсюда следует, что общий множитель всех элементов строки (столбца) можно вынести за знак определителя.
--------------------------------------------
Определитель
-го порядка, по правилу, равный сумме произведений элементов произвольного строки или столбца на соответствующие алгебраические дополнения. Мысленно вычеркнем в определителе 
-го порядка 
-й строчку и 
-й столбец, а из оставшихся элементов создадим определитель(
)-го порядка с сохранением размещения строк и столбцов. Полученный определитель называется минором определителя и обозначается 
Алгебраическое дополнение 
элемента
определителя можно представить в виде
--------------------------------------------
Пример 1.
Задачи. Найти определитель 4-го порядка
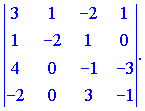
Решение.
Разложим определитель по элементам второго столбца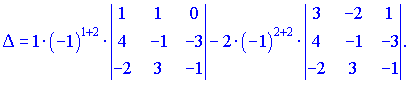 
Первый определитель разложим по первой строкой
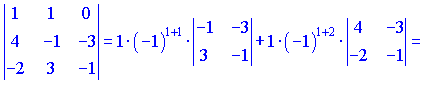
Второй вычислим по правилу
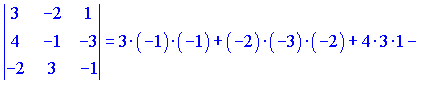
Подставляя в формулу для определителя, получим
Студенческий калькулятор YukhymCALC осуществляет вычисления и выводит результат, быстрее чем Вы сможете ввести соответствующие матрицы. В результате получим следующий результат
*** Матрицы ***
Определитель матрицы
Входные данные
A=(3;1;-2;1)
(1;-2;1;0)
(4;0;-1;-3)
(-2;0;3;-1)
Det(A)=3*(-2*(-1)*(-1)+1*(-3)*0+0*0*3-(0*(-1)*0+1*0*(-1)+(-2)*(-3)*3))-1*(1*(-1)*(-1)+1*(-3)*(-2)+0*4*3-(0*(-1)*(-2)+1*4*(-1)+1*(-3)*3))-2*(1*0*(-1)+(-2)*(-3)*(-2)+0*4*0-(0*0*(-2)+(-2)*4*(-1)+1*(-3)*0))-1*(1*(-1)*(-1)+1*(-3)*(-2)+0*4*3-(0*(-1)*(-2)+1*4*(-1)+1*(-3)*3))=3*(-2+0+0+0+0-18)-1*(1+6+0+0+4+9)-2*(0-12+0+0-8+0)-1*(0-4+0+0+24+0)= 3*(-20)-1*(20)-2*(-20)-1*20=-60-20+40-20=-60
--------------------------------------------
------------------------------
