Решение неоднородных дифференциальных уравнений третьего порядка

Теорию вычислений неоднородных дифференциальных уравнений (ДУ) приводить в данной публикации не будем, из предыдущих уроков Вы можете найти достаточно информации, чтобы найти ответ на вопрос "Как решить неоднородное дифференциальное уравнение?" Степень неоднородного ДУ здесь большой роли не играет, не так уж и много имеется способов, которые позволяют вычислить решение подобных ДУ. Чтобы Вам было легко читать ответы в примерах основной акцент сделан только на методику вычислений и подсказки, которые облегчат вывод конечной функции.

Пример 1. Решить дифференциальное уравнение
Решение: Задано однородное дифференциальное уравнение третьего порядка, причем оно содержит лишь вторую и третью производные и не имеет функции и ее первой производной. В таких случаях применяют метод понижения степени дифференциального уравнения. Для этого вводят параметр - обозначим вторую производную через параметр p

тогда третья производная функции равна

Исходное однородное ДУ упростится к виду

Записываем его в дифференциалах, далее сводим к уравнению с разделенными переменными и находим решение интегрированием

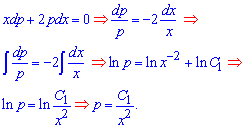
Вспоминаем что параметр это вторая производная функции

поэтому для нахождения формулы самой функции дважды интегрируем найденную дифференциальную зависимость

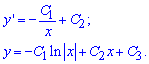
В функции сталые C₁, C₂, C₃ – равны произвольным значениям.
Вот так просто выглядит схема позволяющая найти общее решение однородного дифференциального уравнения методом введения параметра. Следующие задачи более сложные и из них вы научитесь решать неоднородные дифференциальные уравнения третьего порядка. Между однородными и неоднородными ДУ в плане вычислений является некоторое различие, в этом Вы сейчас убедитесь.

Пример 2.Найти общее решение дифференциального уравнения
Решение:Имеем неоднородное дифференциальное уравнение третьего порядка. Поэтому его решение следует искать в вид суммы двух - решения однородного и частного решения неоднородного уравнения

Решим сначала однородное дифференциальное уравнение

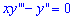
Как видите оно содержит только вторую и третью производную функции и не содержит самой функции. Такого сорта диф. уравнения решают методом введения параметра, что в в свою очередь снижает и упрощает нахождение решения уравнения. На практике это выглядит следующим образом: пусть вторая производная равна определенной функции , тогда третья производная формально будет иметь запись

Рассмотренное однородное ДУ 3 порядка преобразуется к уравнению первого порядка

откуда разделяя переменные находим интеграл
x*dp-p*dx=0;

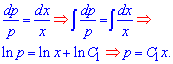
Сталые в таких задачах рекомендуем нумеровать, поскольку решение дифференциального уравнения 3 порядка имеет 3 постоянные, четвертого - 4 и и дальше по аналогии. Теперь возвращаемся к введенному параметру: поскольку вторая производная имеет вид то интегрируя ее один раз мы имеем зависимость для производной функции

и повторным интегрированием находим общий вид однородной функции

Частичное решение уравнения запишем в виде переменной умноженной на логарифм. Это следует из того что правая (неоднородная) часть ДУ равна -1/x и чтобы получить эквивалентную запись

следует решение искать в виде

Найдем коэффициент A, для этого вычислим производные первого и второго порядков

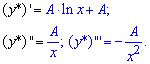
Подставим найденные выражения в исходное дифференциальное уравнение и приравняем коэффициенты при одинаковых степенях x:

Сталая равна -1/2, а решение неоднородного уравнения имеет вид

Общее решение дифференциального уравнения записываем в виде суммы найденных

где C₁, C₂, C₃- произвольные константы которые можно уточнить с задачи Коши.

Пример 3. Найти интеграл ДУ третьего порядка
Решение:Ищем общий интеграл неоднородного ДУ третьего порядка в виде суммы решения однородного и частичного неоднородного уравнения . Сначала для любого типа уравнений начинаем анализировать однородное дифференциальное уравнение

Оно содержит только вторую и третью производные неизвестной пока функции. Вводим замену переменных (параметр): обозначим за вторую производную

Тогда третья производная равна

Такие же преобразования выполняли в предыдущем задании. Это позволяет свести дифференциальное уравнения третьего порядка к уравнению первого порядка вида

Интегрированием находим решение однородного уравнения

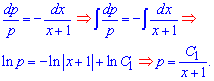
Вспоминаем, что в соответствии с заменой переменных это всего лишь вторая производная

а чтобы найти решение однородного дифференциального уравнения третьего порядка ее нужно дважды проинтегрировать

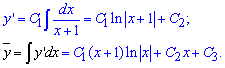
Исходя из вида правой стороны (неоднородной части =x+1), частичное решение уравнения ищем в виде

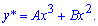
Как знать в каком виде искать частичный решение Вас должны были научить в теоретической части курса дифференциальных уравнений. Если нет, то можем только подсказать, что за функцию выбирают такое выражение чтобы при подстановке в уравнение слагаемое, содержащее старшую производную или моложе был одного порядка (подобный) с неоднородной частью уравнения

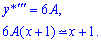
Думаю теперь Вам понятнее, откуда берется вид частного решения. Найдем коэффициенты A, B, для этого вычисляем вторую и третью производную функции

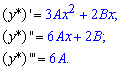
и подставляем в дифференциальное уравнение. После группировки подобных слагаемых получим линейное уравнение

из которого при одинаковых степенях переменной составляем систему уравнений

и находим неизвестные сталые. После их подстановки частичное решение уравнения выражается зависимостью

Общее решение дифференциального уравнения равно сумме однородного и частичного и имеет вид

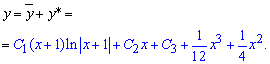
где С₁, С₂, С₃ - произвольные константы.

Пример 4. Решить дифференциальное уравнение
Решение:Имеем неоднородное дифференциальное уравнение третьего порядка решение которого будем находить через сумму . Схема вычислений Вам известна, поэтому переходим к рассмотрению однородного дифференциального уравнения

По стандартной методике вводим параметр
Исходное дифференциальное уравнение примет вид 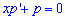, откуда разделив переменные находим интеграл однородного уравнения

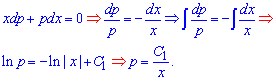
Вспоминаем что параметр равен второй производной
Интегрируя ДУ получим первую производную функции

Повторным интегрированием находим общий интеграл однородного дифференциального уравнения

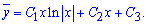
Частичное решение уравнения ищем в виде , так как правая часть равна
Найдем коэффициент A - для этого подставим y* в дифференциальное уравнение и приравняем коэффициент при одинаковых степенях переменной

После подстановки и группировки слагаемых получим зависимость

из которой сталая равна A=8/3.
Таким образом, можем записать частичное решение ДУ

Общее решение дифференциального уравнения равно сумме найденных

где С₁, С₂, С₃ - произвольные константы. Если заданно условие Коши, то их очень легко можем доопределить.

Считаю, что материал Вам пригодится при подготовке к практическим занятиям, модулям или контрольной работе. Здесь не разбирали задачу Коши, однако из предыдущих уроков Вы в целом знаете как это сделать.