Методы (правила) раскрытия неравенств с модулями заключаются в последовательном раскрытии модулей, при этом используют интервалы знакопостоянства подмодульных функций. В конечном варианте получают несколько неравенств из которых и находят интервалы или промежутки, которые удовлетворяют условию задачи.
Перейдем к решению распространенных на практике примеров.
Линейные неравенства с модулями
Под линейными понимаем уравнения, в которых переменная входит в уравнение линейно.
Пример 1. Найти решение неравенства 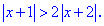
Решение:
Из условия задачи следует, что модули превращаются в ноль при x=-1 и x=-2. Эти точки разбивают числовую ось на интервалы
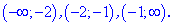
В каждом из этих интервалов решим заданное неравенство. Для этого прежде всего составляем графические рисунки областей знакопостоянства подмодульных функций. Их изображают в виде областей с знаками каждой из функций
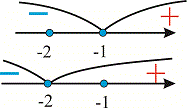
или интервалов со знаками всех функций.
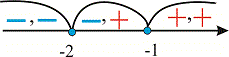
На первом интервале раскрываем модули
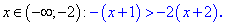
Умножаем обе части на минус единицу, при этом знак в неравенстве поменяется на противоположный. Если Вам до этого правила трудно привыкнуть, то можете перенести каждую из частей за знак, чтобы избавиться минуса. В конечном варианте Вы получите
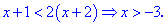
Пересечением множества x>-3 с областью на которой решали уравнения будет интервал (-3;-2). Для тех кому легче искать решения графически можете рисовать пересечение этих областей
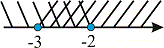
Общие пересечение областей и будет решением. При строгом неровности края не включают. При нестрогое проверяют подстановкой.
На втором интервале получим
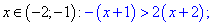
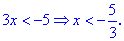
Сечением будет интервал (-2;-5/3). Графически решение будет иметь вид
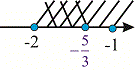
На третьем интервале получим
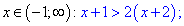
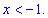
Данное условие не дает решений на искомой областе.
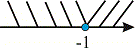
Поскольку два найдены решения (-3;-2) и (-2;-5/3) граничат точкой x=-2, то проверяем и ее.
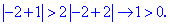
Таким образом точка x=-2 является решением. Общее решение с учетом этого будет выглядеть (-3;5/3).
Пример 2. Найти решение неравенства
|x-2|-|x-3|>=|x-4|
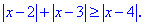
Решение:
Нулями подмодульных функций будут точки x=2, x=3, x=4. При значениях аргументов меньше этих точек подмодульные функции отрицательные, а при больших – положительные.
Точки разбивают действительную ось на четыре интервала. Раскрываем модули согласно интервалов знакопостоянства и решаем неравенства.
1) На первом интервале все подмодульные функции отрицательные, поэтому при раскрытии модулей меняем знак на противоположный.
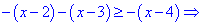
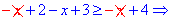
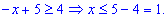
Пересечением найденных значений x с рассматриваемым интервалом будет множество точек
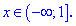
2) На промежутке между точками x=2 и x=3 первая подмодульная функция положительная, вторая и третья – отрицательные. Раскрывая модули, получим
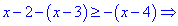
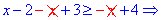
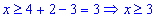
неравенство, которое в пересечении с интервалом, на котором решаем, дает одно решение – x=3.
3) На промежутке между точками x=3 и x=4 первая и вторая подмодульные функции положительные, а третья – отрицательная. На основе этого получим
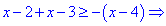
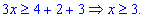
Это условие показывает, что целый промежуток [3;4] будет удовлетворять неравенство с модулями.
4) При значениях x>4 все функции знакоположительные. При раскрытии модулей их знак не меняем.
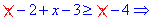
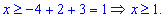
Найденное условие в пересечении с интервалом дает следующее множество решений
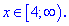
Поскольку неравенство решено на всех интервалах, то остается найти общее всех найденных значений x. Решением будут два интервала
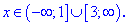
На этом пример решен.
Пример 3. Найти решение неравенства
||x-1|-5|>3-2x
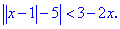
Решение:
Имеем неравенство с модулем от модуля. Такие неравенства раскрывают по мере вложенности модулей, начиная с тех, которые размещены глубже.
Подмодульная функция x-1 преобразуется в нуль в точке x=1. При меньших значениях за 1 она отрицательная и положительная для x>1. На основе этого раскрываем внутренний модуль и рассматриваем неравенство на каждом из интервалов.
Сначала рассмотрим интервал от минус бесконечности до единицы
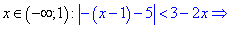
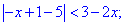
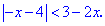
Подмодульная функция равна нулю в точке x=-4. При меньших значениях она знакоположительная, при больших – отрицательная. Раскроем модуль для x<-4:
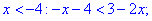
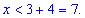
В пересечении с областью, на которой рассматриваем получим множество решений
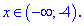
Следующим шагом раскрываем модуль на интервале (-4;1)
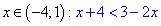
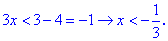
С учетом области раскрытия модуля получим интервал решений
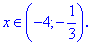
ЗАПОМНИТЕ: если Вы получили в подобных неровностях с модулями два интервала, граничащих общей точкой, то, как правило, она также является решением.
Для этого стоит лишь провести проверку.
В данном случае подставляем точку x=-4.
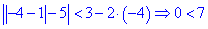
Итак x=-4 является решением.
Раскроем внутренний модуль для x>1
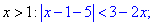
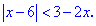
Подмодульная функция отрицательная для x<6.
Раскрывая модуль получим
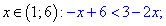
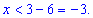
Данное условие в сечении с интервалом (1;6) дает пустое множество решений.
Для x>6 получим неравенство
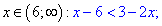
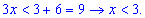
Также решая получили пустое множество.
Учитывая все выше изложенное, единственным решением неравенства с модулями будет следующий интервал.
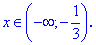
Неравенства с модулями, содержащие квадратные уравнения
Пример 4. Найти решение неравенства
|x^2+3x|>=2-x^2
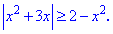
Решение:
Подмодульная функция обращается в нуль в точках x=0, x=-3. Простой подстановкой минус единицы
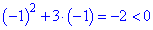
устанавливаем, что она меньше нуля на интервале (-3;0) и положительная за его пределами.
Раскроем модуль в областях где подмодульная функция положительная
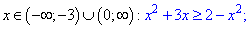
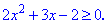
Осталось определить области, где квадратная функция положительная. Для этого определяем корни квадратного уравнения
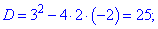
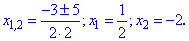
Для удобства подставляем точку x=0, которая принадлежит интервалу (-2;1/2). Функция отрицательная в этом интервале, значит решением будут следующие множества x
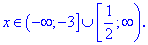
Здесь скобками обозначены края областей с решениями, это сделано сознательно, учитывая следующее правило.
ЗАПОМНИТЕ: Если неравенство с модулями, или простое неравенство является строгим, то края найденных областей не являются решениями, если же неравенства нестроги (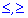 )то края являются решениями (обозначают квадратными скобками).
)то края являются решениями (обозначают квадратными скобками).
Это правило использует многие преподаватели: если задано строгое неравенство, а Вы при вычислениях запишете в решении квадратную скобку ([,]) – они автоматом посчитают это за неправильный ответ. Также при тестировании, если задано нестрогое неравенство с модулями, то среди решений ищите области с квадратными скобками.
На интервале (-3;0) раскрывая модуль меняем знак функции на противоположный
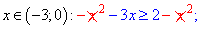
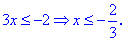
Учитывая область раскрытия неравенства, решение будет иметь вид
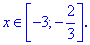
Вместе с предыдущей областью это даст два полуинтервала
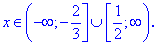
Пример 5. Найти решение неравенства
9x^2-|x-3|>=9x-2
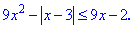
Решение:
Задано нестрогое неравенство, подмодульная функция которого равна нулю в точке x=3. При меньших значениях она отрицательная, при больших – положительная. Раскрываем модуль на интервале x<3.
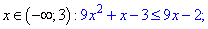
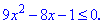
Находим дискриминант уравнения
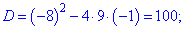
и корни
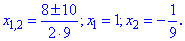
Подставляя точку ноль, выясняем, что на промежутке [-1/9;1] квадратичная функция отрицательна, следовательно промежуток является решением. Далее раскрываем модуль при x>3
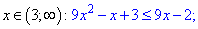
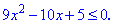
Дискриминант квадратного уравнения
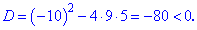
отрицательный, следовательно действительных корней нет.
Единственным решением является промежуток [-1/9;1] .
Давайте выполним данные вычисления в математическом пакете Maple. Анализа подмодульных функций и склеивания областей Вы при этом не увидите, зато без труда получите только правильные решения.
Фрагмент кода в Maple и результаты расчетов приведены ниже
> restart ; - зануление всех переменных
> Q1:=abs(x+1)>2*abs(x+2); - запись уравнения с модулями
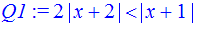
> solve(Q1,x); - решение уравнения с модулями

Здесь RealRange() означает действительный промежуток, Open() - показывает, что края промежутка не включаются (круглые скобки)
> Q2:=abs(x-2)+abs(x-3)>=abs(x-4);
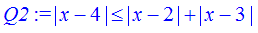
> solve(Q2,x);
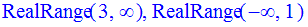
> Q3:=abs(abs(x-1)-5)<3-2*x;
> solve(Q3,x);
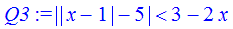
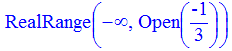
> Q4:=abs(x^2+3*x)>=2-x^2;
> solve(Q4,x);
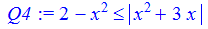
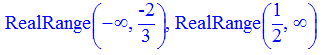
> Q5:=9*x^2-abs(x-3)<=9*x-2;
> solve(Q5,x);
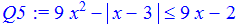
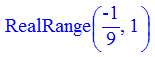
В среде Maple легко реализуется решения иррациональных, логарифмических неравенств с модулями и других. Достаточно лишь ввести заданную неравенство и вызвать команду solve() - решение. Таким образом можно получить решения столь сложных заданий с модулями, что все известные аналитические методы перед ними бессильны.
----------------------------------
Уравнение с модулями требуют большого внимания при решении. Сама меньше невнимательности или ошибка со знаком может привести к лишним решений или их нехватки. При вычислениях можете выполнять проверку методом подстановки. Также можете проверить решения с помощью Maple или других известных Вам математических программ.
Похожие материалы:


