Изменение пределов интегрирования при изменении порядка интегрирования

Продолжаем разбирать готовы примеры на изменение порядка интегрирования в двойном интеграле. Как определять точки пересечения кривых, искать обратные функции и разбивать область интегрирования на подобласти Вам уже должно быть известно из предыдущего урока. Пересмотрите внимательно приведенные задания и хорошо разберите как изменяем пределы при изменении порядка интегрирования.

Пример 3.5 В двойном интеграле изменить порядок интегрирования:

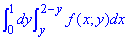
Решение: Построим область интегрирования ограниченную заданными прямыми
0≤y≤1, y≤x≤2-y, здесь x=y и x=2 - y - прямые.
Построим подынтегральную область и заштрихуем, какие нам нужны при вычислениях
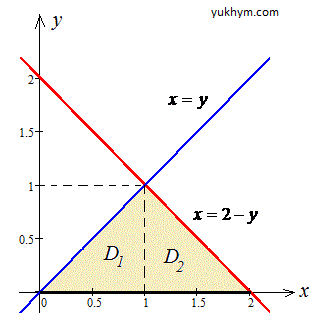Видим, что при изменении порядка интегрирования область интегрирования необходимо разделить на две подобласти
D=D₁+D₂
D₁: 0≤x≤1, 0≤y≤x;
D₂: 1≤x≤2, 0≤y≤2-x.

Это предопределено тем, что нижний предел по игреку у нас постоянная, а верхняя изменяется при прохождении "иксов" от 0 до 2.
При этом двойной интеграл можем заменить суммой двух

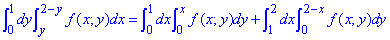
Результат при этом останется одинаковым.

Пример 3.6 Изменить порядок интегрирования в кратном интеграле:

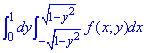
Решение: Построим область интегрирования 
0≤y≤1,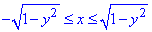
Пределы по переменной "икс" описывают x=√(1-y²), x²=1-y², x²+y²=1² - правый полукруг с центром в начале координат O(0;0) и радиусом 1;
x=-√(1-y²) - левый полукруг с теми же характеристиками.
График области интегрирования приведен ниже

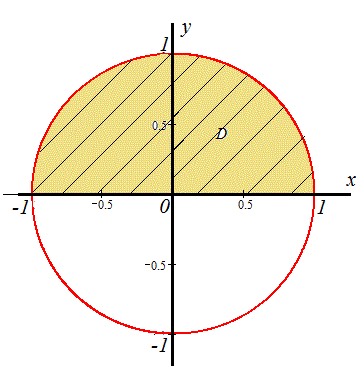
Выражаем полученные функции через переменную y:
x²+y²=1², y=√(1-x²) - верхний полукруг, потому что 0≤y≤1.
Пределы интегралов примут значение:
- 1≤x≤1, 0≤y≤√(1-x²).

Записываем как поменяется двойной интеграл при изменении порядка интегрирования

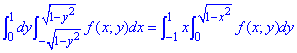
Пример 3.7 Изменить порядок интегрирования:

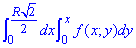
Решение: Область интегрирования в этом примере ограниченна двумя прямыми
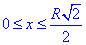, 0≤y≤x, где y=x - прямая.
Кое-кто мог подумать, что где-то должен быть круг, поскольку верхний предел по "икс" содержит R.
Построим область интегрирования


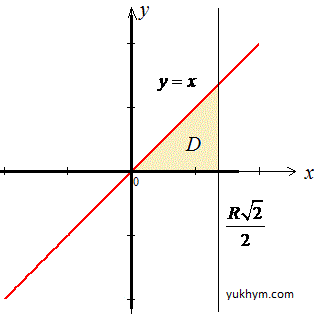
Расставляем пределы при изменении порядка интегрирования
D: 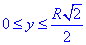, 0≤x≤y.
Двойной интеграл превратится следующим образом:

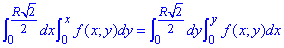
Пример 3.8 Изменить порядок интегрирования в двойном интеграле:

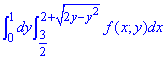
Решение: Распишем область интегрирования ограниченную кривыми
0≤y≤1,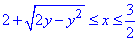
Приведем к каноническому виду запись
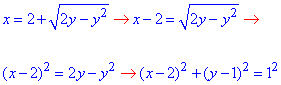- правый полукруг с центром в точке O(2;1) и радиусом R=1.
Подынтегральная область будет иметь следующий вид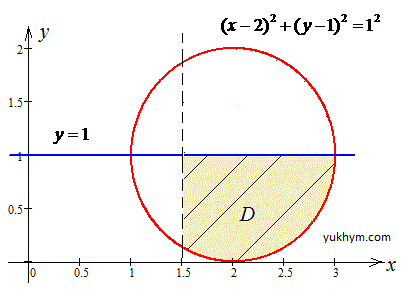

Выражаем полученные функции через переменную x:
(x-2)²+(y-1)²=1, отсюда 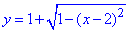(здесь y>0);

Проведем расстановку пределов интегрирования в заданной области D:
1,5≤x≤3,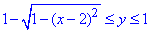

Можем записать интеграл с измененным порядком интегрирования

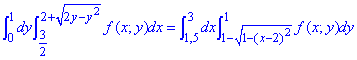
Пример 3.9 Изменить порядок интегрирования:

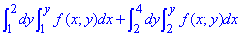
Решение: Видим, что в условии задана сумма двух интегралов.
Следовательно, на плоскости область интегрирования состоит из двух областей
D₁: 1≤y≤2, 1≤x≤y
D₂: 2≤y≤4, 2≤x≤y
где y=x - прямая.
Графически эти области представим рисунком

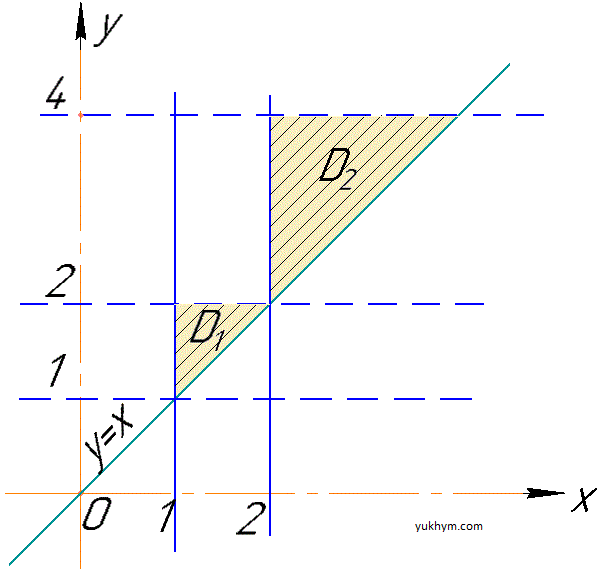
Не пугайтесь подобных заданий, области которые ограничены прямыми легче всего интегрировать.
Расставим пределы в областях D₁, D₂:
D₁: 1≤x≤2, x≤y≤2;
D₂: 2≤x≤4, x≤y≤4.
Внимательно пересмотрите почему именно так изменяются пределы интегрирования.
Выполняем изменение порядка интегрирования

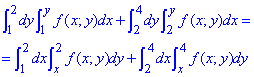
Вот так просто можно вычислять, если хорошо знать теорию и уметь интегрировать на практике.
Учитесь и желаем Вам так же легко решать на практике!