Длина дуги пространственной кривой

Длину дуги получают интегрированием дифференциала дуги от первой точки к конечной. Сложность вычислений заключается в том, что кривая, как правило, заданная двумя или и тремя уравнениями изменения координат по осям, а интегрирование нужно свести к одной координате. Для этого нужно найти дифференциал дуги.
Формулы дифференциалу дуги для пространственных и плоских кривых, заданных явно и параметрически хорошо расписаны.
Их здесь повторять не будем, а лишь выделим цветом в формулах.
Когда известен дифференциал дуги, интеграл вычисляют всеми возможными способами:
непосредственное интегрирование, замена переменных, интегрирования частями.
Часть методов дальше применим для решения заданий.

Пример 1 Найти длину дуги пространственной кривой:
x=3t, y=3t², z=2t³, от точки O(0,0,0) к точке A(3,3,2).
Решение: Найдем производные по переменной t от заданных функций x=x(t), y=y(t) и z=z(t):
x'=3, y'=6t, z'=6t².
Производные нам нужны для нахождения дифференциала дуги ds заданной кривой:

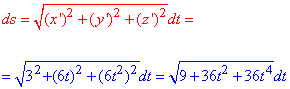
Эта формула справедлива для всех пространственных кривых, заданных параметрически.
Следующим шагом определим пределы интегрирования.
Чтобы их найти нужно в уравнение пространственной кривой

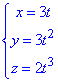
подставить две точки О, А.
Складываем уравнение на определение пределов изменения параметра t:


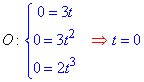
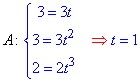
При решении установили, что параметр должен принадлежать интервалу 0≤t≤1.

Вычислим длину дуги заданной кривой, при 0≤t≤1:

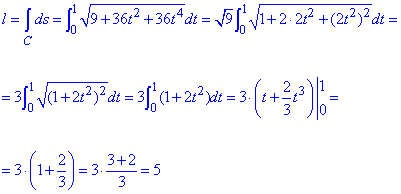
Интеграл найти не трудно, поскольку под корнем легко выделить квадрат, а дальше уже имеем дело с квадратичной функцией, которую легко интегрировать.
Дальше рассмотрим более сложные задания в которых вычисление производных и дифференциала дуги усложняется.

Пример 2 Найти длину дуги пространственной кривой (a>0) :
(x-y)²=a(x+y), x²-y²=9/8-z², от точки O(0,0,0) к точке A(x₀,y₀,z₀).
Решение: В подобных примерах целесообразно сделать замену переменных:

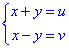
Тогда заданное уравнение (x-y)²=a(x+y) приобретет вид:

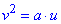
Отсюда

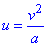
Подобные превращения выполняем для второго уравнения кривой
x²-y²=9/8-z², или (x-y)(x+y)=9/8-z²:

отсюда
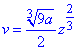(1).
Имеем 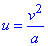, получим:
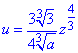(2).
Найдем производные по переменной z от функций u=u(z) и v=v(z):
после упрощений получим такие конечные значения

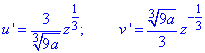
Запишем как изменяется z от точки O(0,0,0) к точке A(x₀, y₀, z₀):
0≤z≤z₀.
Следующим шагом найдем дифференциал дуги ds по формуле: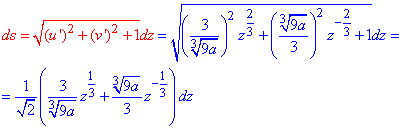

Под корнем выделили полный квадрат, поэтому дифференциал упростился.

Через интеграл вычисляем длину дуги кривой:

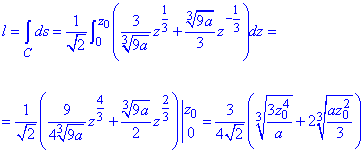
Найти интеграл в этом случае тоже не складывает больших трудностей.

Пример 3 Найти длину дуги пространственной кривой (a>0) :

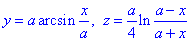
от точки O(0,0,0) к точке A(x₀, y₀, z₀).
Решение: Превратим заданные функции так, чтобы они выражались через переменную y: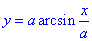

отсюда получим

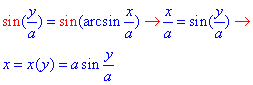
Для вычисления обратной функции к двум сторонам зависимости применили синус преобразование.
Дальше найденное значение обратной функции x(y) и подставляем во второе уравнение пространственной кривой


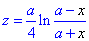
то есть

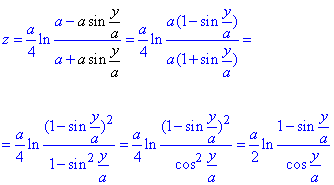
Окончательно получим

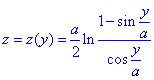
Значение функций в точке A(x₀, y₀, z₀):

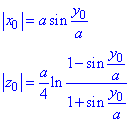
Найдем производные по переменной y функций x=x(y), z=z(y):

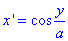
За свойством логарифма превратим логарифм дроби в разницу логарифмов

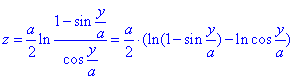
Такой прием поможет при вычислении производной составленной функции

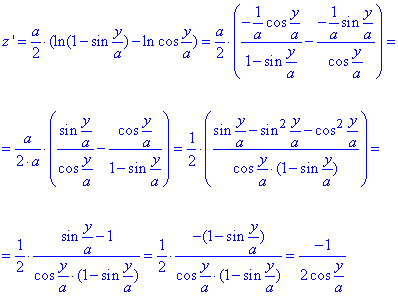
Запишем пределы интегрирования y, когда точка проходит значение от O(0,0,0) к A(x₀, y₀, z₀):
0≤y≤y₀.
Дифференциал дуги ds кривой вычислим по формуле:

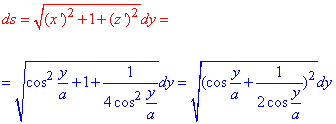
Длину дуги пространственной кривой найдем по формуле:

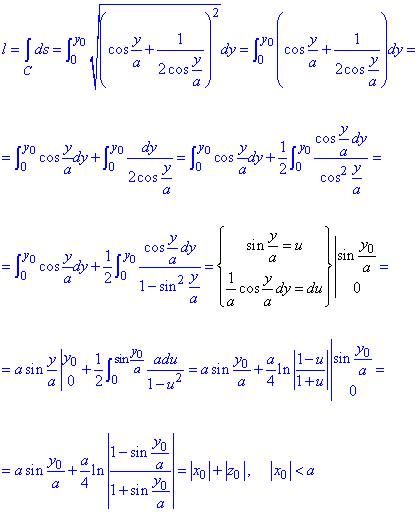
В интеграле сделали замену переменных и интегрировали частями.

Пример 4 Вычислить длину дуги пространственной кривой (a>0, c>0) :
x²+y²=cz, y/x=tg (z/c), от точки O(0,0,0) к точке A(x₀, y₀, z₀).
Решение: Перейдем к полярной системе координат с помощью формул перехода:

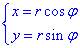
Превращаем первое уравнение кривой

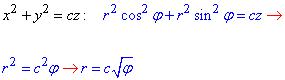
дальше второе

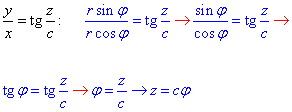
Из формул видим насколько проще стали уравнения кривой.
Запишем все три пространственные координаты через параметр угла φ:

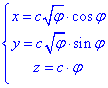
здесь переменная пробегает значение 0≤φ≤z₀/c, поскольку φ=z/c.
Запишем производные по переменной φ для функций x=x(φ), y=y(φ) но z=z(φ):

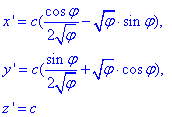
Вычислим дифференциал дуги ds кривой по формуле:

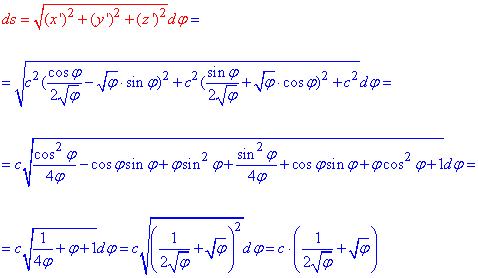
Не забывайте в подобных заданиях выделять полный квадрат под корнем.
Без этого Вы не сможете найти интеграла.
Через интеграл найдем длину дуги пространственной кривой:

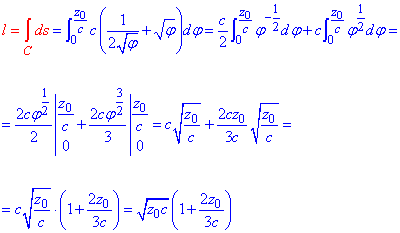
Из приведенных примеров можно сделать вывод, что сложность вычисления криволинейных интегралов имеет место лишь в выборе системы координат, нахождении производных и дифференциалов дуг.
Найти интеграл в большинстве случаев достаточно легко, сложные задания, как правило, преподаватели Вам не дадут вычислять.