1)
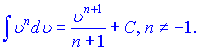
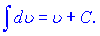
2) 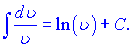
3)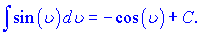
4) 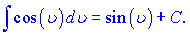
5)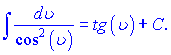
6)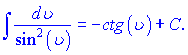
7)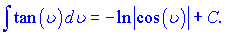
8)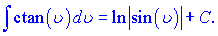
9)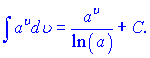
10)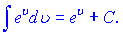
11)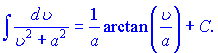
12) 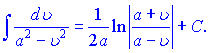
13) 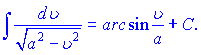
14) 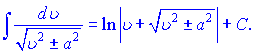
15) 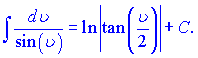
16) 
17) 
18) 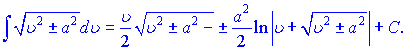
В наведених формулах a - константа, v- незалежна змінна або будь-яка (диференційовна) фунція від незалежної змінної. Ящо Ви займаєтеся складними розрахунками і наведених формул Вам недостатньо, то рекомендуємо завантажити "Таблиці інтегралів" Градштейна, Рижика.
]]>Розв'яжемо декілька прикладів для засвоєння методу безпосереднього інтегрування.
Приклад 1. Обчислити невизначені інтеграли за таблицею.
а) Розкриваємо дужки, щоб отримати поліном, а далі інтегруємо за відомою формулою
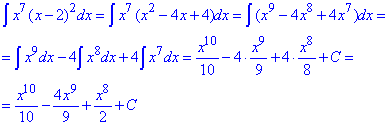
б) Інтеграл замінимо сумою інтегралів, які знаходимо за таблицею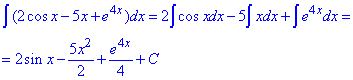
Приклад 2. Знайти інтеграли
а) 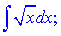
Розв'язання: Даний інтеграл можна переписати у вигляді
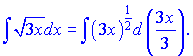
Його знаходимо за формулою степеневих функцій при 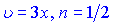 . Згідно цієї формули отримаємо
. Згідно цієї формули отримаємо
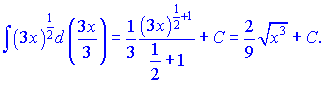
Нічого важкого в роботі з дробовими показниками немає, головне уважність.
б) 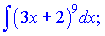
Розв'язання: Інтеграл обчислюємо за 1 формулою таблиці інтегралів при 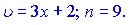
Внісши дужку під диференціал, обчислення інтегралу дещо спроститься
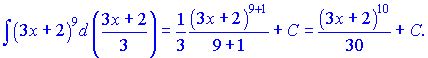
Така техніка в простих випадках дозволяє не проводити заміни змінних.
в) 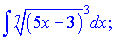
Розв'язання:Тут перетворюємо корінь до показника та застосовуємо 1 формулу з аблиці інтегралів. Для неї вибирамо
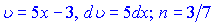
Подальші перетворення дозволяють швидко знайти неозначений інтеграл
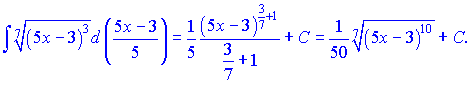
г) 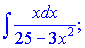
Розв'язання:Підінтегральна функція може бути зведений до формули (2) таблиці при
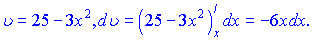
В результаті інтегрування фунції отримаємо
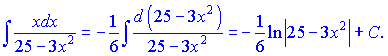
д) 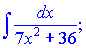
Розв'язок. Інтеграли такого вигляду знаходимо за формулою (10) . Для цього перетворюємо знаменник дробу та вносимо корінь з семи під диференціал
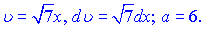
Згідно формул інтегрування неозначений інтеграл рівний арктангенсу
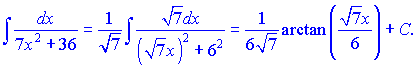
Приклад 1. Обчислити невизначені інтеграли за таблицею.
а) Розкриваємо дужки, щоб отримати поліном, а далі інтегруємо за відомою формулою
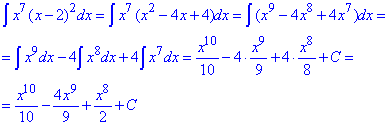
б) Інтеграл замінимо сумою інтегралів, які знаходимо за таблицею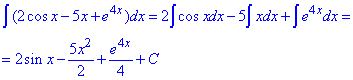
Далі будуть розглянуті завдання, які навчать зводити функції під усі формули таблиці інтеграів. Також Ви познайомитися з рядом методик, без яких складні на вигляд функції в анлітичний спосіб проінтегрувати неможливо. Залишайтеся з нами і навчання математичних дисциплін Вам буде легким і зрозумілим.
]]>Наведу Вам декілька прикладів для ознайомлення з інтегруванням методом розкладу.
Приклад 1. Знайти інтеграли
а) 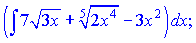
Розв'язання: Інтеграл переписуємо у вигляді суми простих степеневих функцій, після чого кожну з них інтегруємо
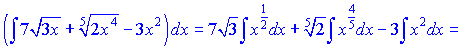
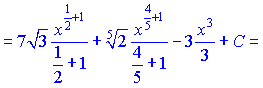
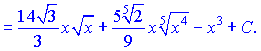
б) 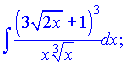
Розв'язання:Піднесемо до третього степеня дужку в чисельнику
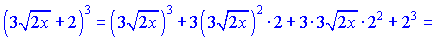
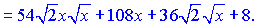
Поділимо знайдений чисельник на знаменник та розпишемо результат через степеневі залежності
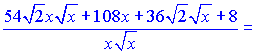
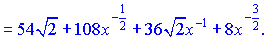
Далі проінтегруємо отримані доданки
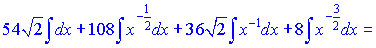
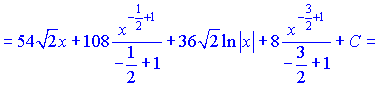
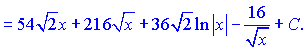
в) 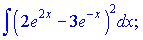
Розв'язання: Піднесемо до квадрату вираз, що містить експоненти та знайдемо неозначений інтеграл за табличною формулою
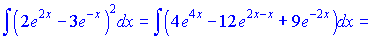
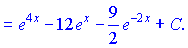
Експоненту з усіх функцій, напевно найлегше інтегрувати.
г) 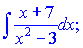
Розв'язання:Розкладемо дробову функцію у вигляді суми двох
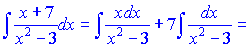
Далі вніссши змінну в першому інтегралі під диференціал, а в другому записавши знаменник у вигляді різниці квадратів, прийдемо до табличних формул інтегрування. Це дає можливість швидко отримати у відповідь логарифми наступних функцій
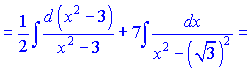
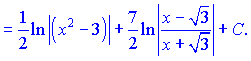
Дану методику рекомендуємо вивчити, в практичних завданнях наведена схема зустрічається доволі часто.
д) 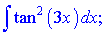
Розв'язання:Проведемо тригонометричні маніпуляції з тангенсом, щоб звести його під формли інтегрування.
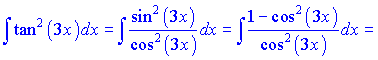
В результаті неозначений інтеграл рівний квадрату тангенса мінус змінна
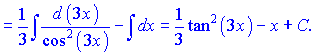
е) 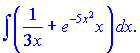
Розв'язок.Розпишемо підінтегральний вираз у вигляді суми окремих доданків
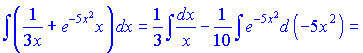
Далі знаходимо відповідні функціям формули та інтегруємо
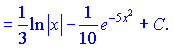
Таким чином, якщо мати таблицю основних інтегралів під рукою, то розв'язування подібних прикладів – це вже справа навичків. Чим більше подібних прикладів Ви розв'яжете, тим легше буде в освоєнні подальших розділів інтегрування.
]]>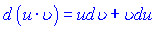 інтегруванням двох частин рівності одержуємо формулу інтегрування частинами
інтегруванням двох частин рівності одержуємо формулу інтегрування частинами
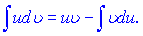
За цією формулою знаходження інтеграла 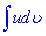 зводиться до знаходження іншого інтеграла
зводиться до знаходження іншого інтеграла 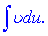 Застосовувати цю формулу потрібно в тих випадках, коли інтеграл
Застосовувати цю формулу потрібно в тих випадках, коли інтеграл 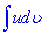 легко знаходитися. Якщо неправильно вибрати
легко знаходитися. Якщо неправильно вибрати 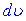 , то завдання навпаки може ускладнитись. Для застосування формули інтегрування частинами до інтегралу
, то завдання навпаки може ускладнитись. Для застосування формули інтегрування частинами до інтегралу 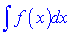 необхідно підінтегральний вираз
необхідно підінтегральний вираз 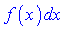 представити в вигляді добутку двох множників
представити в вигляді добутку двох множників 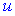 та
та 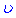 . За диференціал
. За диференціал 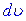 завжди вибирають такий вираз, що містить
завжди вибирають такий вираз, що містить 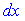 . Його інтегруванням можна знайти
. Його інтегруванням можна знайти 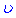 . За
. За 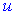 в більшості випадків приймається функція, яка при диференціюванні спрощується.
в більшості випадків приймається функція, яка при диференціюванні спрощується.
В такий спосіб на перший погляд важкі і незрозумілі, з точки зору обчислень, інтеграли можна швидко звести до табличного вигляду.
Поширені приклади інтегрування частинами
Приклад 1. Обчислити невизначені інтеграли методом інтегрування частинами.
а) якщо на практиці Ви зустрінете добуток полінома на синус чи косинус, то останні і слід вносити під диференціал
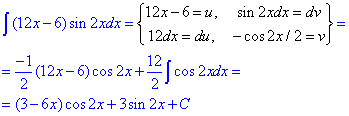
б) Перший раз арктангенс залишаємо, а за dv позначаємо dx. Далі обчислюємо похідну арктангенса та підставляємо.
подальші заміни для інтегрування частинами розбирайте самостійно з формули
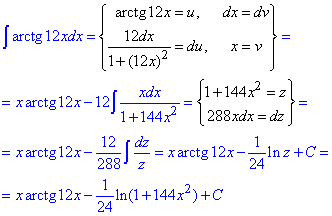
Приклад 2. Обчислити інтеграли
а) 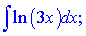
Розв'язок: Даний інтеграл один з класичних в курсі вищої математики. Функції 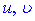 підбираємо таким чином
підбираємо таким чином
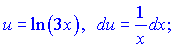
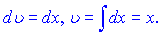
Згідно формул інтегрування частинами маємо
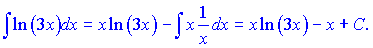
б) 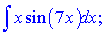
Розв'язок: Для даного інтеграла функції 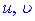 для підстановки вибираємо у вигляді
для підстановки вибираємо у вигляді
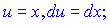
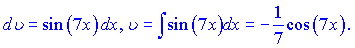
За формулою отримаємо
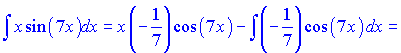
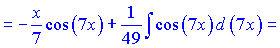
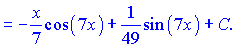
На цьому прикладі добре видно ефективність методу підстановки. Ніяка інша методика не дозволяє так швидко обчислити інтеграл.
в) 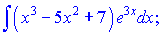
Розв'язок: Для заданого заміни вибираємо наступними
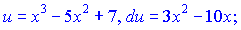
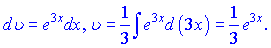
Підставляємо в інтеграл та обчислюємо його
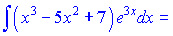
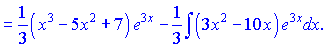
Бачимо, що знову отримали інтеграл до якого потрібно застосувати правило інтегрування частинами. За схемою вибираємо функцію
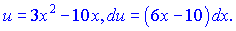
Формли для 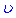 беремо з попереднього інтегрування. Підставляємо в інтеграл та знаходимо
беремо з попереднього інтегрування. Підставляємо в інтеграл та знаходимо
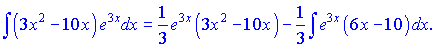
Останній доданок потребує повторного інтегрування частинами. Для цього записуємо заміну змінних
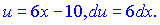
Друга змінна залишається без змін. Залишився один крок до повного обчислення значення інтегралу.
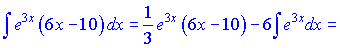
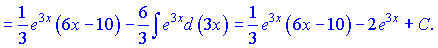
Всі внутрішні інтеграли підставляємо у початкову формулу
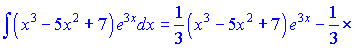
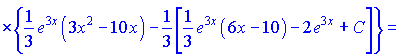
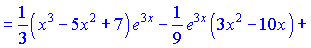
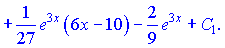
Це і є відповіддю до завдання.
г) 
Розв'язок: Вибираємо функції 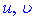 для застосування правила заміни змінних у вигляді
для застосування правила заміни змінних у вигляді
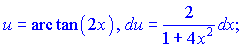
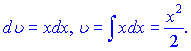
За правилами інтегрування отримаємо
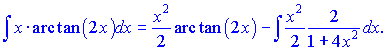
Останній інтеграл знайдемо за правилом розкладу, для цього чисельник доповнюємо до вигляду знаменника
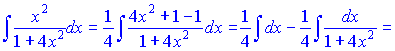

Остаточно інтеграл матиме вигляд
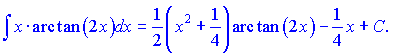
д) 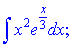
Розв'язок: За функції u,v вибираємо наступні
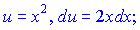
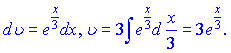
За правилом інтегрування частинами знаходимо неозначений інтеграл
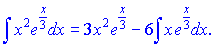
Для останнього доданку необхідно повторно застосувати інтегрування частинами.
Першу функцію вибираємо так
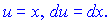
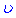 - залишається без змін. Обчислюємо інтеграл
- залишається без змін. Обчислюємо інтеграл
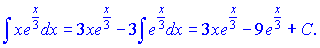
Значення інтегралу підставимо в попередній вираз
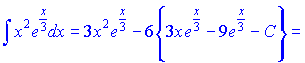
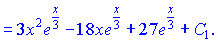
В цьому завдання застосовувати правило доводилося повторно. Це не складно, адже Ви тепер знаєте, яку робити заміну змінних при інтегруванні частинами.
е) 
Розв'язок:Вибираємо функції u,v для заміни змінних наступними
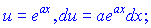
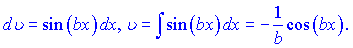
Здійснимо інтегрування частинами
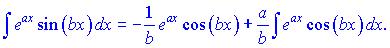
Далі u залишаємо без змін, а v знаходимо інтегруванням
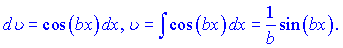
Повторно інтегруємо косинус
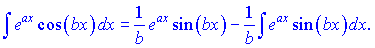
Необхідно зауважити, що шуканий інтеграл та останній однакові. Позначимо їх
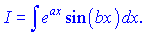
При цьому отримуємо рекурентну залежність
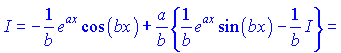
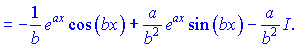
З рівняння виражаємо невідомий інтеграл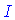
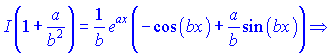
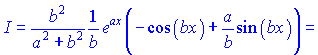
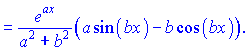
Інтеграли на подобі останнього зустрічаються доволі рідко, проте вимагають особливої уваги при їх розв'язанні. Найменша помилка може призвести до ускладнення інтегралу і красивого рівняння Ви можете не отримати. Тому будьте уважні при обчисленнях.
Сподіваюсь, що з даного уроку Ви багато потрібного для себе почерпнули. Практикуйте в розв'язуванні задач і до зустрічі в наступних уроках.
Приклад 1. При інтегруванні дробової функції необхідно в знаменнику корінь квадратний перетворити на показник, далі розділити чисельник на знаменник і отримані доданки проінтегрувати. Якщо не вдаватися в дрібні розписування то в кінцевому варіанті інтеграл прийме значення
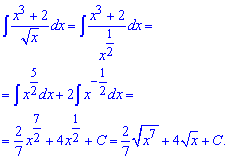
Для більшості студентів хід обчислень має бути зрозумілим, якщо перехід між останніми двома рядками Ви не можете здійснити то почніть з того, що відкрийте або роздрукуйте основні формули інтегрування.
Приклад 2. Маємо під інтегралом дріб від синус функцій, спершу спрощуємо діленням чисельника на знаменник. Далі знаменник дробу в другому інтегралі розписуємо за теоремою косинуса, а синус вносимо під диференціал. Таким чином перейдемо до нової змінної t=cos(x) в інтегруванні.
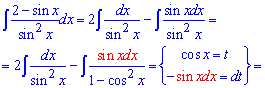
Другий інтеграл за табличними формулами рівний логарифму від частки простих множників знаменника
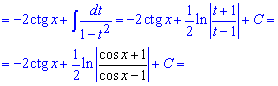
Повертаємося до заміни, яку виконували. На цьому інтегрування можна було і завершити, а можна записати в компактнішому вигляді. Але для цього необхідно знати або мати під рукою тригонометричні формули та властивості логарифма.
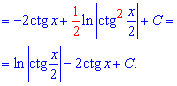
Приклад 3. Для обчислення інтегралу запишемо знаменник дробу у вигляді різниці квадратів, а далі помножимо на мінус одиницю та зведемо до табличного логарифма від частки простих множників
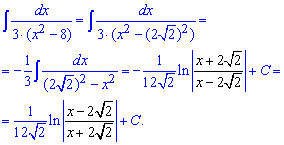
Мінус перед логарифмом загнали в показник функції, тому дріб під логарифмом в кінцевому варіанті обернутий.
Приклад 4. Дуже повчальне завдання на інтегрування, побільше би таких на контрольних чи тестах. Якщо б в степені мали 3 чи 4, то підносити ще хоч якось було б можна. Тут же стоїть 10, тому підносити до 10 степеня мало хто захоче. Для спрощення вираз в дужках в подібних завданнях на інтегрування позначте за нову змінну t=2x+5. Далі застосовуємо табличну формулу і після того, як проінтегрували не забуваємо підставити заміну.
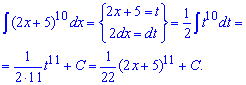
Добре запам'ятайте схему обчислення цього інтегралу.
Приклад 5. На перший погляд складний інтеграл, однак схема обчислень достатньо проста. Позначимо арккосинус за нову змінну t=arccos(x) та запишемо її диференціал. Як бачите диференціал рівний dx розділити на знаменник. І така схема більшості складних прикладів на неозначені інтеграли. Тому Ваше основне завдання – навчитися бачити заміни змінних, схеми зведення під табличну формулу, вдало вибирати функцію під правило інтегрування частинами. А для цього потрібно розв'язати чимало інтегралів, тож краще вчитися на готових відповідях+самосійна робота.
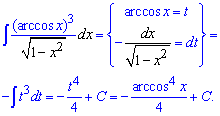
Приклад 6. Під інтегралом маємо дробову ірраціональну функцію від експоненти. Для обчислення інтегралу позначимо функцію під коренем за нову змінну. Також перетворимо експоненту в чисельнику та знайдемо диференціал від нової змінної.
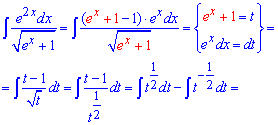
Після таких дій отриманий інтеграл за складністю нічим не поступатиметься першому з розглянутих прикладів. Після інтегрування не забуваємо повернутися до виконаної заміни змінних.
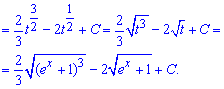
Приклад 7. Для обчислення цього та інших прикладів Ви повинні знати, що похідна від логарифма рівна одиниці розділеній на змінну. Таким чином більшості інтегралів де міститься показникові функція від логарифма та «ікс» в знаменнику за нову змінну вибирайте логарифм t=ln(x). В результаті інтеграл суттєво спростися і отримаємо компактний результат
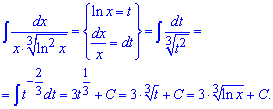
Решта відповідей в наступних матеріалах. Пам'ятайте, що такого роду приклади задають на контрольній чи тестах та уважно розбирайте відповіді до завдань.
Готові розв'язки контрольної з інтегрування
]]>Приклад 1. Якщо перед інтегралом мали б множником "ікс", то його можна було б внести під диференціал і провести заміну змінних. Однак інтеграл дещо складніший, тому вирази в дужках підносимо до кубу, а далі виконуємо інтегрування кожного з доданків.
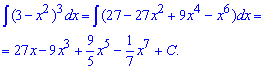
Приклад 2. Задано дробову функцію в знаменнику якої міститься ірраціональність. Щоб її позбутися функцію під коренем позначимо за нову змінну, далі знаходимо її диференціал та підставляємо в інтеграл. Після незначних маніпуляцій з показниками обчислюємо інтеграл, і замість змінної підставляємо виконану заміну.
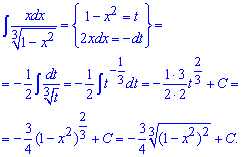
Приклад 3. Хто часто обчислює інтеграли або добре знає теорію інтегралів, то в цьому та подібних завданнях за нову змінну вибирає логарифм. При диференціюванні логарифма отримуємо одиницю розділену на "ікс", що значно спрощує подальше інтегрування. Вкінці не забувайте в прикладах на заміну змінних перейти до початкової змінної "ікс".
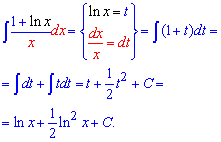
Приклад 4. Виконуємо інтегрування частинами, для цього синус вносимо під диференціал
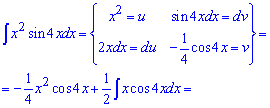
Після першого разу знову отримаємо інтеграл, який обчислюємо інтегруванням частинами.
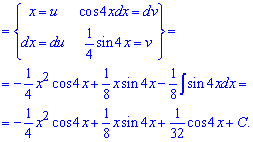
Приклад 5. Маємо завдання під правило інтегрування частинами u*dv. За змінну вибираємо експоненту, а синус вносимо під диференціал.
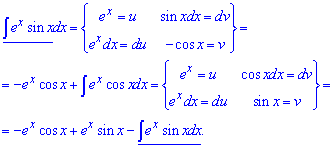
Після повторного інтегрування частинами прийдемо до рекурентної формули, з якої і визначаємо інтеграл.
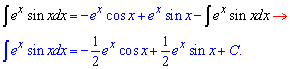
Приклад 6. В цьому інтегралі квадратний тричлен, що стоїть в знаменнику треба звести до суми чи різниці квадратів.
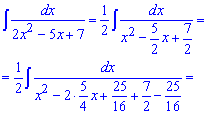
Далі за формулами інтегрування отримаємо арктангенс.
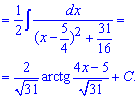
Приклад 7. Інтегрування добутку тригонометричних функцій дається не всім студентам, і тут потрібно враховувати як степені, так і сам вигляд функцій. В цьому прикладі один косинус потрібно внести під диференціал і звести завдання до інтегрування функції від синуса.
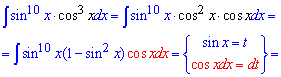
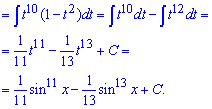
Сам інтеграл не складний і знаходиться за правилом для степеневих функцій.
Приклад 8. Якщо маємо синуси чи косинуси у показниках більших одиниці, то за тригонометричними формулами їх треба порозписувати аж до першого степеня. Далі застосовують формули інтегрування синусів або косинусів.
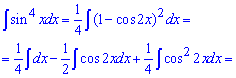
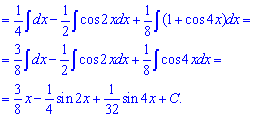
Приклад 9. Щоб знайти інтеграл від дробової функції спершу розділимо чисельник на знаменник, та отриманий в остачі дріб розпишемо на найпростіші дроби. Після цього, використовуючи формули інтегрування, обчислюємо значення кожного з інтегралів.
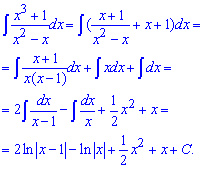
Приклад 10. Маємо інтеграл від дробової функції
![]()
Записуємо її через найпростіші дроби першого та другого типів.
![]()
Далі зводимо дроби під спільний знаменник та з умови рівності чисельників складаємо систему лінійних рівнянь для обчислення невідомих сталих.
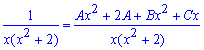
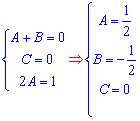
Після її розв'язування повертаємося до дробу, підставляємо сталі та виконуємо інтегрування.
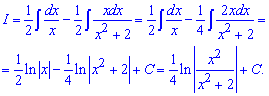
Приклад 11. Маємо інтеграл від дробової ірраціональної функції. Для розкриття ірраціональності виконуємо наступну заміну змінних під інтегралом
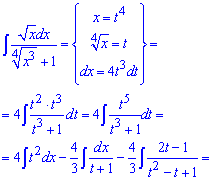
В результаті прийдемо до дробової раціональної функції під інтегралом, яку розписавши на прості дроби легко проінтегрувати
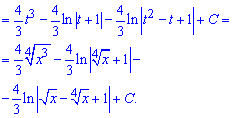
Приклад 12. В цьому завданні для поз буття ірраціональності під інтегралом необхідно використати одну відому хитрість. Вона полягає в тому, що провівши наступну заміну змінних прийдемо до раціональної функції від косинуса.
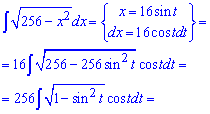
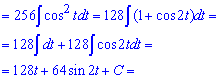
Після інтегрування повертаємося до виконаної заміни і на цьому обчислення можна завершити. Однак, якщо мати під рукою тригонометричні формули то відповідь можна дещо спростити ізаписати в більш компактному вигляді.
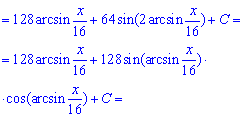
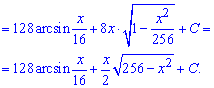
Приклад 13. Маємо в знаменнику раціональну функцію від косинуса і синуса. Такі інтеграли слід знаходити через універсальну тригонометричну заміну t=tg(x/2)
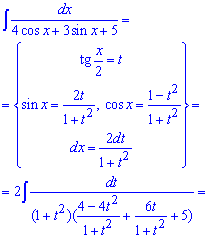
Після підстановки формул синус та косинуса через тангенс половини кута підінтегральна функція перетвориться до дробової, в знаменнику якої матимемо квадратний тричлен. Його зводимо до квадрату виразу, що містить змінну та інтегруємо за правилом для степеневих функцій.
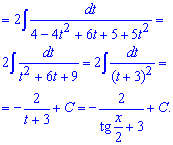
Після інтегрування не забуваємо, що наше t=tg(x/2) і підставляємо його у формулу інтегралу.
На цьому добірка прикладів завершується, більше прикладів Ви знайдете в категорії інтегрування. Для збільшення бази готових інтегралів надсилайте цікаві приклади на [email protected] або замовляйте у нас розв'язання контрольних робіт та модулів.
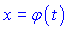 , де
, де 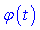 –диференційована функція від t. Після цього знаходять
–диференційована функція від t. Після цього знаходять 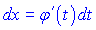 і інтеграл
і інтеграл 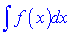 перетворюють до вигляду
перетворюють до вигляду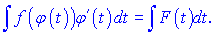
Якщо одержаний інтеграл з новою змінною інтегрування t буде знайдено, то перетворивши результат в зворотньому напрямку до змінної x, використовуючи залежність
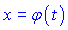 , відшукаємо вираз заданого інтегралу.
, відшукаємо вираз заданого інтегралу.На перший погляд вище наведені формулювання методу виглядають не такими простими, як хотілося. Але повірте, що за даним методом стоять не такі важкі математичні перетворення. Розглянувши приклади, які наведені нижче і попрактикувавши на інших, у Вас все получиться. Якщо ні – надсилайте важкі приклади нам, а ми зі своєї сторони спробуємо їх розв'язати і опублікувати в наступних статтях. Отже переходимо до прикладів.
Приклад 1. Обчислити невизначені інтеграли методом заміни змінної.
а) 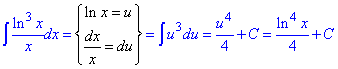
б) 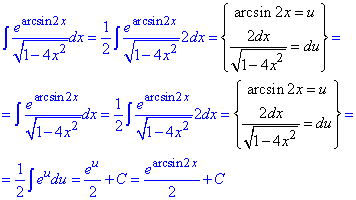
Приклад 2. Обчислити інтеграли
а) 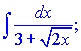
Розв'язок. Перш ніж читати наведені відповіді Ви повинні хоч частово ознайомитис з теорією інтеграів. Лише тоді наведена інформаці буде для Вас корисно та повчально.
Вибираємо за нову змінну t такий вираз, що дозволяє позбутися кореня в знаменнику
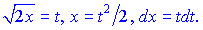
Заcтосовуючи це до інтеграла отримаємо:
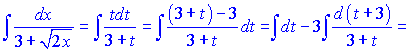
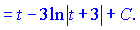
Залишилося не забути в останній вираз підставити заміну, яку зробили на початку 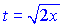
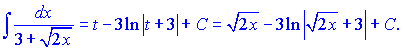
Варто зазначити, що єдиної методики заміни змінної немає. Кожен вибирає заміну так, як підказує досвід і практика. Для даного прикладу за змінну t можна взяти цілий знаменник. Давайте зробимо це і поглянемо наскільки зміниться складність обчислень.
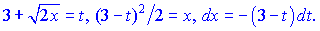
Робимо заміну змінних в інтегралі та обчислюємо його
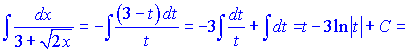
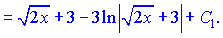
Ви можливо зауважили, що після другої заміни змінних інтеграл, порівняно з першою заміною, відрізняється на константу, яка рівна 3. Це не є помилкою, оскільки неозначені інтеграли можуть відрізнятися на константу.
Як бачимо, обидві заміни змінних в даному випадку ефективні.
б) 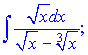
Розв'язок.Вводимо таку підстановку, щоб добувалися корені в знаменнику 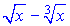
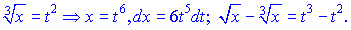
Підставляємо в інтеграл
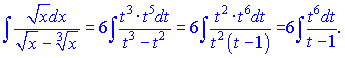
Поділимо чисельник t6 на знаменник t-1, щоб отримати правильний дріб. Після ділення отримаємо розклад
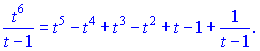
Підставимо в інтеграл та проінтегруємо
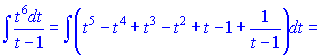
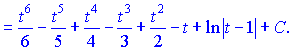
Повертаємося назад до змінної x
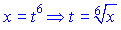
та замінюємо в інтегралі
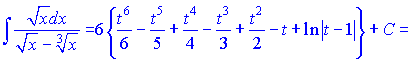
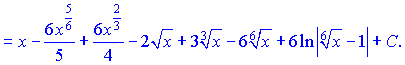
Результат отримали досить швидко і заміна змінних в цьому випадку дуже допомогла.
в) 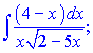
Розв'язок.Для підінтегральної функції вводимо підстановку, яка дозволяє позбутися кореня в знаменнику
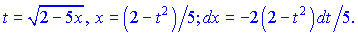
Проводимо інтегрування
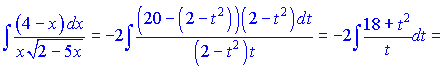
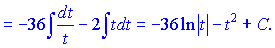
Ряд перетворень пропущено, Ви їх можете виконати самостійно.
Повертаємося до змінної x
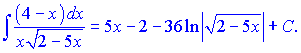
Це і є кінцеве значення неозначеного інтегралу.
г) 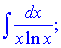
Розв'язок.За нову змінну в подібних завданнях необхідно вибирати логарифм
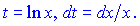
Підставимо в інтеграл та знайдемо його значення
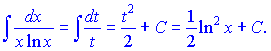
д) 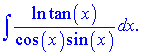
Розв'язок.Позначимо через нову змінну чисельник дробу ln(tan(x))
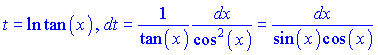
і підставимо в інтеграл
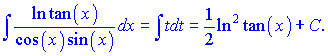
На перший погляд складний інтеграл методом заміни змінних зведено до простого табличного інтегралу. Саме головне в методі – вдало підібрати заміну змінних. Подальше розв'язування, як правило, не надто громіздке і, при добрих знаннях попереднього матеріалу , швидко приводить до кінцевого результату.
Даний урок думаю приніс Вам певну ясність в реалізації методу підстановки. Збагачуйте практичні знання і до зустрічі в наступних уроках.
Приклад 1. Перетворюємо корінь знаменнику на показник, далі виконуємо ділення і після цього інтегруємо згідно формул інтегрування степеневих функцій
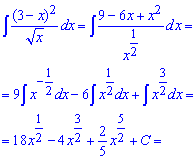
Після інтегрування відповідь переписуємо через корені
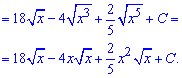
Приклад 2. Розбиваємо підінтегральну функцію на дві, першу з яких знаходимо за правилом інтегрування показникових функцій
![]()
Приклад 3. Перетворюємо підінтегральну функцію так, щоб під коренем при змінній коефіцієнт був рівний одиниці. За формулами інтегрування отримаємо арксинус
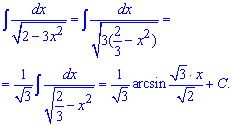
Заміна змінних під інтегралом
Приклад 4. Чисельник дробу перетворюємо таким чином, щоб він став рівним диференціалу від знаменника. Це дозволить застосувати заміну змінних та спростити інтегрування. В результаті отримаємо логарифм від функції, що знаходиться в знаменнику вихідного інтегралу
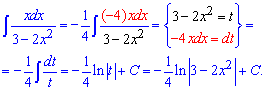
Приклад 5. В такого роду завданнях на інтеграли слід знати чому рівні похідні від тригонометричних функцій. В даному випадку, якщо за нову змінну вибрати котангенс та про диференціювати його то при підстановці отримаємо інтеграл від лінійної функції. Його знайти може учень 11 класу, проте не кожен учень зуміє побачити наведену заміну.
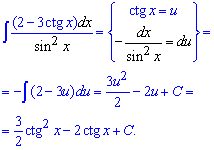
Після інтегрування всюди замість змінної підставляємо котангенс.
Приклад 6. Маємо дробову функцію, яка являє собою синус розділений на експоненту в степені косинус. Щоб перейти до другої основи інтегрування за змінну виберемо показник експоненти, продиференціюємо змінну та підставимо в інтеграл. При таких діях отримаємо інтеграл від експоненти з від'ємним показником. Його обчислюємо за табличною формулою
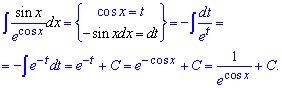
Приклад 7. Одиницю мінус логарифм позначимо за нову змінну, похідна нам дасть потрібну частину інтегралу. Після підстановки прийдемо до інтегрування степеневої функції з від'ємним показником.
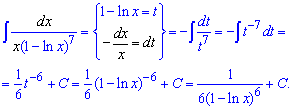
Вкінці не забувайте в усіх прикладах, де виконували заміну, підставляти початкову функцію (1-ln(x)).
Приклад 8. Декілька наступних завдань потрібно розв'язувати за правилом інтегрування частинами udv. За dv вибирають функцію, яка за 1 два роки приведе до рекурентної формули або після ряду повторного застосування правила інтегрування частинами отримаємо кінцеву відповідь. Тут косинус потрійного аргументу потрібно внести під диференціал
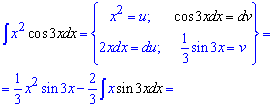
Повторно застосовуємо інтегрування частинами
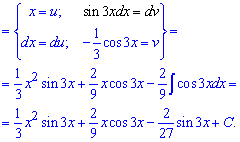
Як бачите нічого складного в інтегруванні немає, головне слідкувати за знаками синуса, косинуса.
Приклад 9. Завжди де бачите добуток експоненти на будь-яку функцію знайте, що доведеться інтегрувати частинами. Причому за dv вибираємо експоненту на dx.
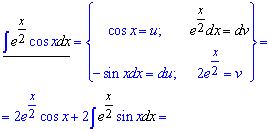
Після повторного інтегрування частинами отримаємо
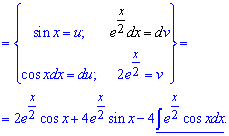
Слід зазначити, що далі інтегрувати ми не будемо. В такому отримали рекурентну формулу (справа і зліва від знаку рівності маємо потрібний інтеграл).
![]()
Переносимо невідомі по один знак рівності та обчислюємо інтеграл.
![]()
В подібних завданнях при інтегралі можуть бути не тільки константи, а й функції.
Приклад 10. Інтегруємо частинами, за функцію вибираємо арктангенс, за диференціал dv=x*dx. Після диференціювання арктангенса та інтегрування частинами другий інтеграл спроститься до двох табличних формул.
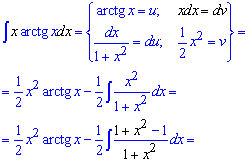
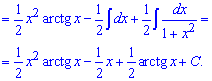
Приклад 11. Інтегруємо методом заміни змінних. Змінну вибираємо таким чином, щоб в показнику експоненти позбутися ірраціональності. Далі приходимо до інтегрування частинами та загнавши експоненту під диференціал експоненту застосовуємо формули udv
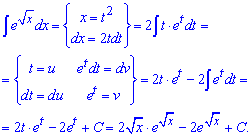
Приклад 12. В таких завданнях квадратний тричлен в знаменнику слід записати у вигляді різниці або суми квадратів. Далі прийдемо до інтегралу, що в підсумку дає арктангенс
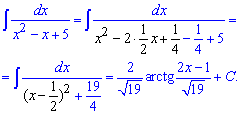
Приклад 13. Виділяємо квадрати під коренем та зводимо інтеграл до арксинуса.
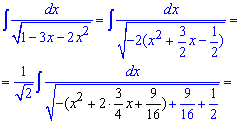
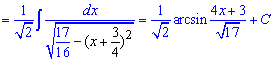
Ось і кінець уроку, в ньому при мінімальних поясненнях Ви отримали якісні схеми та поради для обчислення невизначених інтегралів. Користуйтеся ними та застосовуйте на практиці.
При групуванні уважно слідкуйте за сумою дробів, в такій простій операції левова частка помилок при інтегруванні, принаймні для тих хто дійшов хоч до якоїсь відповіді. Також запам'ятайте схему обчислень цього та попереднього прикладів, вони є поширеними на контрольних і тестах.
Готові розв'язки контрольної з інтегрування
]]>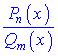
називається раціональним, якщо чисельник Pn(x) та знаменник Qm(x) є многочлени.
Раціональні дроби поділяють на правильні та неправильні. Дріб називається правильним, якщо найвищий показник степеня чисельника n менший від найвищого степеня знаменника m. У іншому випадку дріб називається неправильним. Інтегруються лише правильні дроби. Неправильний раціональний дріб у якого степінь чисельника вищий або дорівнює степені знаменника можна діленням чисельника на знаменник звести до cуми многочлена та правильного раціонального дробу.
Типи раціональних дробів
Найпростішими раціональними дробами називають наступні
І. 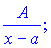
ІІ. 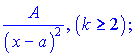
ІІІ. 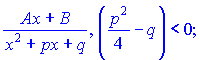
ІV. 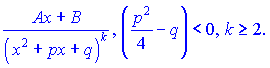
Умова 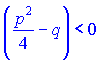 означає, що квадратне рівняння x2+px+q не має дійсних коренів. В іншому випадку його можна розкласти на множники і звести до 1 типу.
означає, що квадратне рівняння x2+px+q не має дійсних коренів. В іншому випадку його можна розкласти на множники і звести до 1 типу.
Для всіх чотирьох груп існують правила зведення до табличного вигляду і інтегрування. Інтеграли І та ІІ типу знаходять методом безпосереднього інтегрування
І. 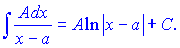
ІІ. 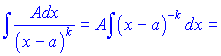
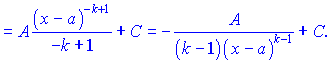
При інтегруванні найпростішого дробу ІІІ-го типу потрібно виконати наступні перетворення.
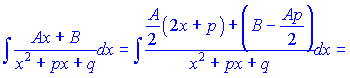
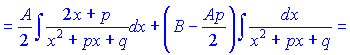
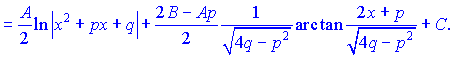
Інтеграл від найпростішого дробу IV-го типу шляхом повторного інтегрування частинами можна звести до інтегралу від найпростішого дробу III-го типу. Інтеграл від дробово-раціональної функції 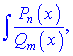 де
де 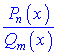 – правильний дріб, можна звести методом розкладу на доданки, які легко інтегруються за основними формулами інтегрування. Усі правильні раціональні дроби розкладаються на суму найпростіших раціональних дробів, коефіцієнти яких можна знайти методом невизначених коефіцієнтів. Кінцевий вигляд найпростіших дробів залежить від коренів знаменника Qm(x) та їх кратності.
– правильний дріб, можна звести методом розкладу на доданки, які легко інтегруються за основними формулами інтегрування. Усі правильні раціональні дроби розкладаються на суму найпростіших раціональних дробів, коефіцієнти яких можна знайти методом невизначених коефіцієнтів. Кінцевий вигляд найпростіших дробів залежить від коренів знаменника Qm(x) та їх кратності.
Можливі наступні варіанти поліномів:
1. Корені знаменника – дійсні та різні числа, тобто
Qm(x)=(x-a)(x-b)...(x-d)
Тоді дріб розкладається на суму найпростіших дробів І-го типу
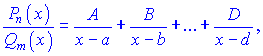
де A, B, ..., D – невідомі коефіцієнти. Їх знаходять наступним чином: доданки справа зводять до спільного знаменника, а потім прирівнюють отримані коефіцієнти при степенях x чисельника з тими, які містить поліном Pn(x).
2. Корені знаменника дійсні числа, деякі з них кратні k
Qm(x)=(x-a)...(x-b)k.
В цьому випадку правильний дріб розкладається на суму найпростіших дробів І-го та ІІ-го типів:
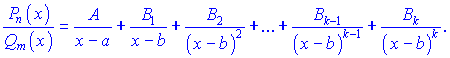
Невідомі коефіцієнти A, B1, B2,..., Bk шукаємо методом невизначених оефіцієнтів.
3. Деякі корені знаменника дійсні числа, деякі з них кратні. Крім того знаменник містить один або декілька квадратних тричленів, які не розкладаються на множники
Qm(x)=(x-a)...(x-b)k...(x2+px+q).
Тоді дріб розкладається на суму найпростіших дробів І-го, ІІ-го та ІІІ-го типів
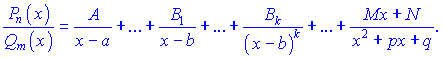
Тут A, B1, B2,..., Bk, M, N – невідомі коефіцієнти, які шукають за схемою поданою вище (неозначені коефіцієнти).
4. Цей випадок відрізняється від попереднього тим, що в знаменнику дробів квадратні тричлени бувають в степенях >=2. В таких випадках можемо отримати суму найпростіших дробів І-ІV-го типів. Вони найскладніші, але наведеними вище методами їх розв'язування можливе.
Практична сторона інтегрування раціональних дробів детально розглянута в наступній статті.
Нижче будуть наведені завдання на дроби І- ІІІ типів, які наочно покажуть як використовувати правила інтегрування для дробових функцій.
Приклад 1. Обчислити інтеграли
а) 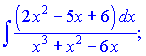
Розв'язок. Оскільки степінь чисельника менший за степінь знаменника, то підінтегральна функція – правильний дріб. Знаменник x3+x2-6x можна розкласти на множники
x(x-2)(x+3)
Таким чином дріб розкладається на суму доданків першого типу (І)
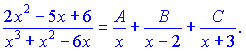
Невідомі коефіцієнти A, B, C знаходимо методом невизначених коефіцієнтів. Для цього праву частину отриманої тільки що нерівності зводимо до спільного знаменника
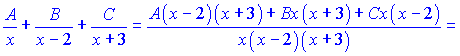
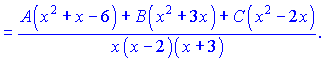
Прирівнюємо чисельники для знаходження невідомих коефіцієнтів
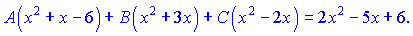
Ця рівність виконується коли коефіцієнти при однакових степенях x рівні між собою. З цієї умови отримуємо систему лінійних рівнянь для визначення невідомих A, B, C
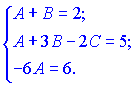
Розв'язуючи її знаходимо невідомі коефіцієнти
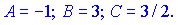
Тоді підінтегральна функція набуде вигляду
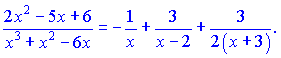
Інтегруючи дроби за знаком рівності отримаємо значення неозначеного інтегралу
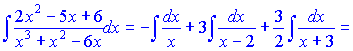
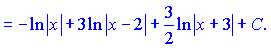
Нічого складного в розв'язування такого сорту прикладів немає, лише правильно скласти і розв'язати систему лінійних рівнянь для визначення невідомих.
б) 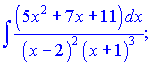
Розв'язок.Підінтегральна функція є правильним дробом, знаменник якого має дійсні корені. Такий дріб розкладається на суму найпростіших дробів І-го та ІІ-го типів методом невизначених коефіцієнтів
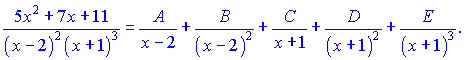
Визначимо невідомі онстанти A, B, C, D, E, для цього праву частину зводимо до спільного знаменника.
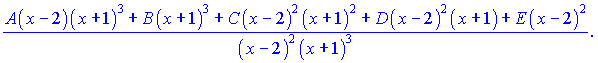
Розкриваємо дужки і прирівнюємо коефіцієнти при однакових степенях в чисельниках. Отримаємо наступну систему лінійних рівнянь
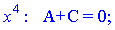
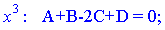
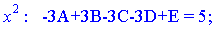
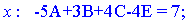
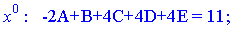
Можемо розв'язувати систему рівнянь методом Гауса, але це важкий шлях.
Є інший спосіб отримання системи рівнянь для визначення невідомих. Чисельники справа і зліва повинні бути рівні для всіх а. Ця особливість дещо спрощує розв'язування системи рівнянь. Як правило, за точки x в першу чергу беруть корені рівняння та 0. В нашому випаду це були б значення x=-1; x=2. Нуль вибирають за рахунок простоти обчислень.
Розв'язавши отриману вище систему лінійних рівнянь, отримаємо наступні значення невідомих:
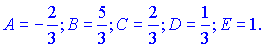
Інтегруємо підінтегральну функцію, врахувавши знайдені константи
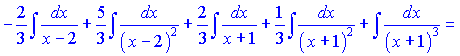
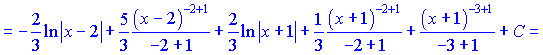
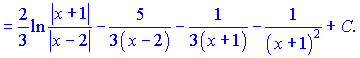
в) 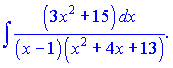
Розв'язок. Знаменник містить квадратний тричлен і множник. Даний дріб за правилами розкладається на суму дробів І-го та ІІІ-го типів:
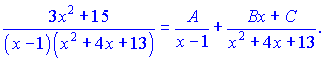
Звівши до спільного знаменника, отримаємо:
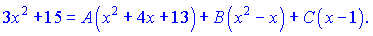
Можемо прирівняти коефіцієнти при однакових степенях, але поступимо інакше, щоб навчитися використовувати іншу методику. Для цього підставимо корінь x=1 в ліву і праву частину рівності, отримаємо
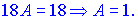
Щоб позбутися невідомої B підставимо x=0
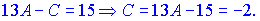
Для знаходження невідомої C випишемо невідомі при x

В такий спосіб, не виписуючи систем лінійних рівнянь і не розв'язуючи їх, можна досить швидко знайти невідомі константи.
Підставивши знайдені значення, розпишемо вихідний інтеграл через суму
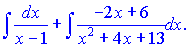
Перший доданок інтегрується за табличною формулою і дає модуль логарифма
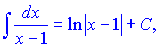
до другого застосовуємо заміну
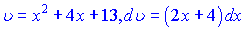
та зводимо до суми двох
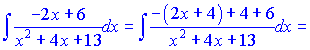
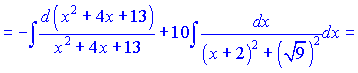
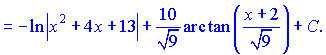
Просумувавши отримані інтеграли, остаточно отримаємо розв'язок
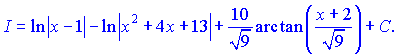
Розв'язавши декілька прикладів на кожен з типів Вам стане зрозуміліше, до якого типу зводити інтеграли і який приблизно буде результат. Тож практикуйте самостійно, вдосконалюйте навики і отримуйте лише вірні розв'язки.