Пример 1. Если бы перед интегралом имели множителем "икс", то его можно было бы внести под дифференциал и провести замену переменных.
Однако интеграл более сложен, потому выражения в скобках подносим к кубу, а дальше выполняем интегрирование каждого из слагаемых.
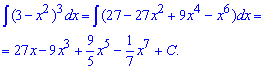
Пример 2. Задана дробная функция в знаменателе которой содержится иррациональность. Чтобы от нее избавиться функцию под корнем обозначим за новую переменную, дальше находим ее дифференциал и подставляем в интеграл. После незначительных манипуляций с показателями вычисляем интеграл, и вместо переменной подставляем выполненную замену.
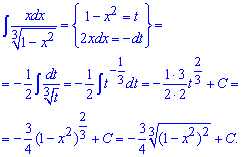
Пример 3. Кто часто вычисляет интегралы или хорошо знает теорию интегралов, то в этом и подобных заданиях за новую переменную выбирает логарифм. При дифференцировании логарифма получаем единицу разделенную на "икс", который значительно упрощает дальнейшее интегрирование.
Напоследок не забывайте в примерах на замену переменных перейти к начальной переменной "икс".
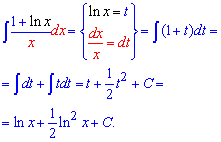
Пример 4. Выполняем интегрирование частями, для этого синус вносим под дифференциал
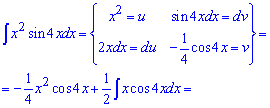
После первого раза опять получим интеграл, который вычисляем интегрированием частями.
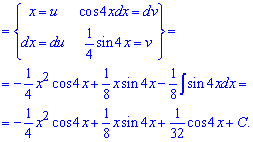
Пример 5. Имеем задание под правило интегрирования частями u*dv. За переменную выбираем экспоненту, а синус вносим под дифференциал.
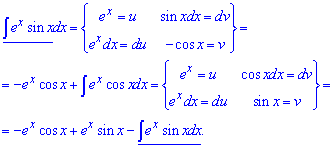
После повторного интегрирования частями придем к рекуррентной формуле, из которой и определяем интеграл.
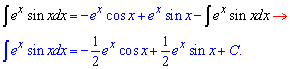
Пример 6. В этом интеграле квадратный трехчлен, который стоит в знаменателе надо возвести к сумме или разнице квадратов.
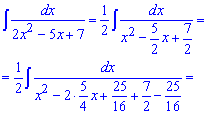
Дальше за формулами интегрирования получим арктангенс.
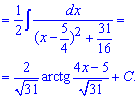
Пример 7. Интегрирование произведения тригонометрических функций дается не всем студентам, и здесь нужно учитывать как степени, так и сам вид функций.
В этом примере один косинус нужно внести под дифференциал и свести задание к интегрированию функции от синуса.
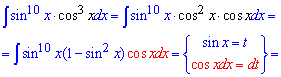
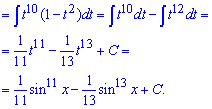
Сам интеграл не сложен и находится по правилу степенных функций .
Пример 8. Если имеем синусы или косинусы в показателях больше единицы, то за тригонометрическими формулами их надо расписать вплоть до первой степени. Дальше применяют формулы интегрирования синусов или косинусов.
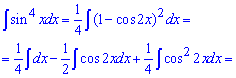
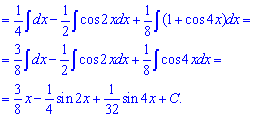
Пример 9. Чтобы найти интеграл от дробной функции сначала разделим числитель на знаменатель, и полученную в остатке дробь распишем на самые простые дроби. После этого, используя формулы интегрирования, вычисляем значение каждого из интегралов.
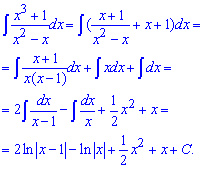
Пример 10. Имеем интеграл от дробной функции
Записываем ее через самые простые дроби первого и второго типов.
Дальше возводим дроби под общий знаменатель и из условия равенства числителей складываем систему линейных уравнений для вычисления неизвестных постоянных.
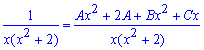
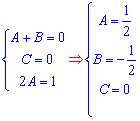
После ее решения возвращаемся к дроби, подставляем сталые и выполняем интегрирование.
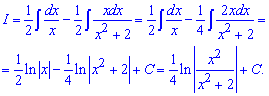
Пример 11. Имеем интеграл от дробной иррациональной функции. Для раскрытия иррациональности выполняем следующую замену переменных под интегралом
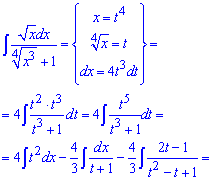
В результате придем к дробной рациональной функции под интегралом, которую расписав на простые дроби легко проинтегрировать.
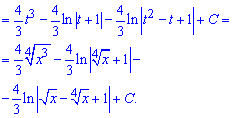
Пример 12. В этом задании чтобы избавиться иррациональности под интегралом необходимо использовать одну известную схему.
Она заключается в том, что проведя следующую замену переменных придем к рациональной функции от косинуса.
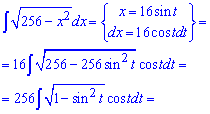
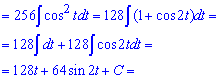
После интегрирования возвращаемся к выполненной замене и на этом вычислению можно завершить.
Однако, если иметь под рукой тригонометрические формулы то ответ можно упростить и записать в более компактном виде.
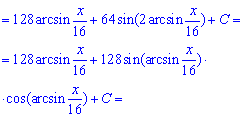
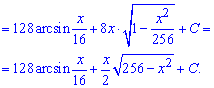
Пример 13. Имеем в знаменателе рациональную функцию от косинуса и синуса. Такие интегралы следует находить через универсальную тригонометрическую замену t=tg (x/2)
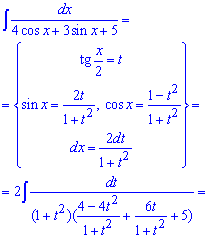
После подстановки формул синус и косинуса через тангенс половины кута подинтегральная функция превратится к дробной, в знаменателе которой будем иметь квадратный трехчлен. Его возводим к квадрату выражения, которое содержит переменную и интегрируем по правилу степенных функций .
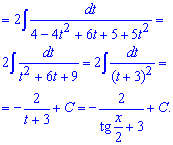
После интегрирования не забываем, что наше t=tg (x/2) и подставляем его в формулу интеграла.
На этом подборка примеров завершается, больше примеров Вы найдете в категории интегрирования.
Для увеличения базы готовых интегралов присылайте интересные примеры на [email protected] или заказывайте у нас решение контрольных и расчетных работ.
Пример 1. Нужно найти интеграл от дробной иррациональной функции. Для этого сначала корни превратим в показатели
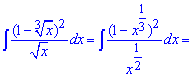
Далее в числителе возведем дужку к квадрату. Остается разделить числитель на знаменатель и по правилу суммы проинтегрировать каждое из слагаемых.
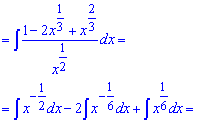
В результате интеграл примет значение
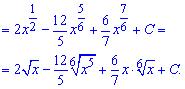
Пример 2. Вычисляем интеграл от произведения показательной функции на экспоненту. Для этого оба множителя вносим под общий степень и применяем формулуинтегрирования
Пример 3. Для нахождения интеграла под корнем выполним преобразования, которые позволят получить при переменной коэффициент единицу. Это удобно для прямого применения табличной формулы
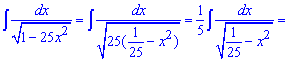
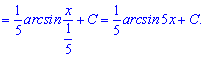
Поскольку имеем дело с неопределенными интегралами то следует не забывать добавить в конце постоянную.
Замена переменных под интегралом
Пример 4. Для вычисления интеграла обозначим дужку в знаменателе за новую переменную. Далее найдем dx и подставим в интеграл
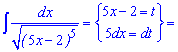
В конце не забываем вернуться к замене, которую делали в начале.
Пример 5. Для вычисления интеграла от дроби тригонометрических функций следует выполнить следующую замену. Ее трудно заметить, однако производная от котангенса равна минус единицы разделенной на синус в квадрате, то есть знаменателе дроби. Таким образом интеграл преобразуем к следующему
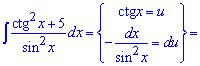
После интегрирования подставляем сделанную замену.
Пример 6. Нужно найти интеграл от экспоненты умноженной на иррациональную функцию от экспоненты. Для упрощения возьмем выражение под корнем за новую переменную и найдем остальные необходимых для интегрирования величины.
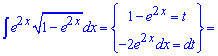
После интегрирования возвращаемся к замене.
Пример 7. На вид сложный интеграл имеет простое решение. Все что для Вас создает трудности при интегрировании отмечайте за новую переменную. В этом задании особенность вносит функция под синусом. Ее и обозначим за u, и найдем дифференциал du
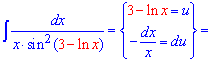
Интеграл упростится до табличного значения, после его нахождения выполняем замену переменных.
Как только Вы изучите приведенные схемы интегрирование и сможете самостоятельно найти подобные интегралы - тогда контрольная работа не будет для Вас чем то сложным в обучении. Если в обучении встречаются сложные интегралы, которые Вы не в силах решить, помните - мы всегда готовы оказать помощь. Это предложение актуально как для студентов стационарной формы обучения, так и для заочников и школьников. Те кто заочно учатся получают очень слабую теоретическую базу для понимания всей силы формул интегрирования.
Готовые решения контрольной по интегрированию
]]>Интегрирование рациональных дробей
Пример 15. Сначала раскладываем знаменатель на простые множители
В результате функция под интеграл сведется к простейшим дробям с неизвестными постоянными.
Для их вычисления сводим слагаемые под общий знаменатель
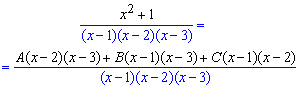
При равных знаменателях расписываем и приравниваем коэффициенты при одинаковых степенях "икс" по обе стороны знака равенства.
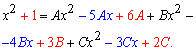
В результате получим систему линейных алгебраических уравнений (СЛАУ) для вычисления постоянных A, B, C
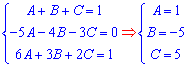
Решение СЛАУ можете находить методом Крамера если большинство коэффициентов ненулевые, или методом Гаусса в противном случае. При известных постоянных переходим к интегрированию.
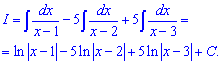
Пример 16. Знаменатель дроби раскладываем на простые множители. Один из корней находим среди делителей свободного члена (4={4;-4;2;-2;1;-1}).
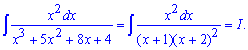
Раскладываем дробь на слагаемые с неизвестными постоянными
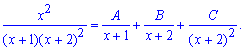
Далее сводим под общий знаменатель
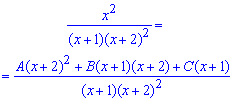
и после раскрытия скобок в числителе группируем слагаемые
Далее составляем систему уравнений и вычисляем коэффициенты
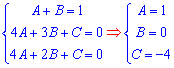
Постоянные подставляем в интеграл и находим его значение
Методика возведения под табличные интегралы
Пример 17. В данном задании необходимо в числителе дробной функции выделить множитель, который получим при расписании знаменателя к разнице или сумме квадратов. Далее его вносим под дифференциал и интегрируем
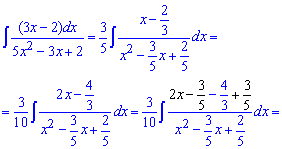
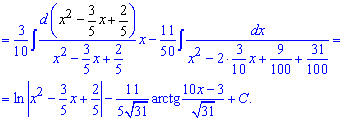
Здесь пропущено переход от последнего интеграла к арктангенсу, поэтому попробуйте преобразовать самостоятельно. Практическая работа никому еще не повредила, а многих даже изменила в лучшую сторону.
Пример 18. Чтобы избавиться от иррациональности в числителе введем степенную замену переменных. При этом интеграл разложится на две слагаемые, которые имеют простой для интегрирования вид
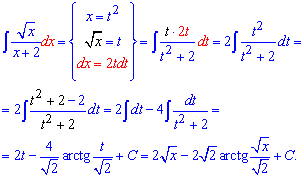
Если посмотреть на ответ то виглидит все просто и понятно, но как только приходится иметь дело с подобным заданием самостоятельно сразу руки опускаются и все знания куда-то исчезают. Чтобы такого не было решайте аналогичные примеры самостоятельно. Их можно придумать на основе этих примеров, или поискать например в Демидовича.
Пример 19. В знаменателе имеем иррациональную функцию, поэтому чтобы ее раскрыть за новую переменную выбираем такую, чтобы при ее подстановке не иметь корней. В результате замены интеграл сведется к табличной формуле
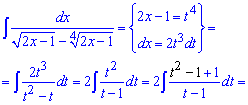
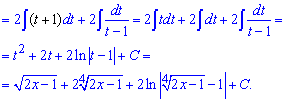
После интегрирования возвращаемся к выполненной замене.
Остальные ответы в следующих материалах. Помните что такого рода примеры задают на контрольной или тестах и внимательно разбирайте ответы к заданиям.
Готовые решения контрольных с интегрирования
]]>Пример 8. Интеграл находим по правилу интегрирования частями int(u*dv)=u*v-int(v*du). Здесь главное правильно выбрать функции под правило. (Для себя запомните что за dv если возможно выбирают периодические функции или такие, которые при дифференцировании с точностью до множителя дают сами себя - экспонента). В этом интеграле нужно синус внести под дифференциал
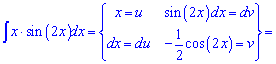
Дальнейшее интегрирование достаточно простое и на деталях останавливаться не будем.
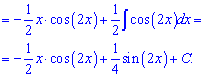
Пример 9.Снова нужно применять правило интегрирования по частям u*dv. Здесь имеем произведение периодической функции на экспоненту, поэтому что лучше вносить под дифференциал выбирать Вам. Можно как экспоненту, так и косинус (в каждом варианте получим рекуррентную формулу).
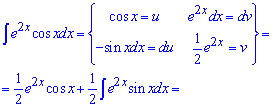
Применяем интегрирование по частям повторно
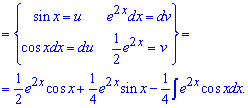
Пришли к рекуррентной формуле. Если записать интеграл который искали и результат вычислений то получим два подобные слагаемые
Группируем их и находим искомый интеграл
Пример 10. Имеем готовую запись интеграла под правило u*dv. Находим du и выполняем интегрирование
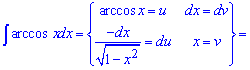
Сводим второй интеграл под табличную формулу и вычисляем его
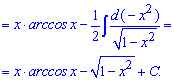
Пример 11. Обозначим за новую переменную cos(ln(x))=u і найдем du, затем внесением под дифференциал
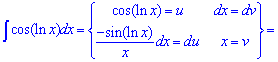
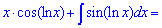
К интегралу повторно применяем правило интегрирования по частям
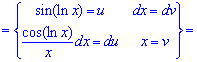
Пришли к рекуррентной формуле
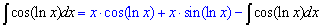
с которой и вычисляем неизвестный интеграл
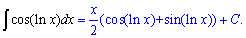
Пример 12. Для нахождения интеграла выделим в знаменателе полный квадрат. Далее сведя знаменатель к известной формуле интегрирования получим арктангенс
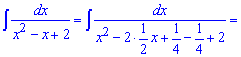
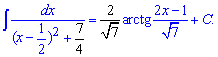
Хорошо запомните порядок чередования множителей. Единица разделена на корень из свободного члена фигурирует перед арктангенсом, также этот множитель присутствует в арктангенс перед переменной.
Пример 13. Дело имеем с подобным интегралом, только в знаменателе квадратичная зависимость находится под корнем. Выделяем полный квадрат и сводим под формулу интегрирования, которая дает логарифм
Вот такие бывают примеры на контрольной или тестах. Хорошо запомните основные схемы интегрирования.
Если не можете решить интеграл сами, тогда обращайтесь за помощью.
Готовые решения контрольной по интегрированию
]]>1)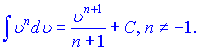
2)
3)
4)
5)
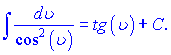
6)
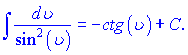
7)
8)
9)
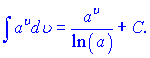
10)
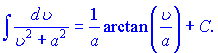
11)
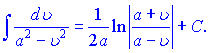
12)
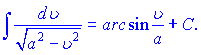
13)
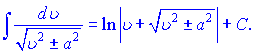
14)
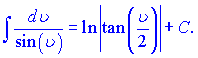
15)
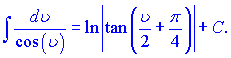
16) 
17)
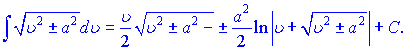
В приведенных формулах 
- константа, 
- независимая переменная или любая (дифференцируемая) функция от независимой переменной.
Пример 15. Мы пришли к интегрированию дробно-рациональных функций. Они занимают особое место среди интегралов, поскольку требуют много времени на вычисление и помогают преподавателям проверить Ваши знания не только по интегрированию. Для упрощения функции под интегралом добавим и вычтем в числителе выражение, которое позволит разбить функцию под интегралом на две простые
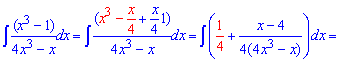
В результате один интеграл находим довольно быстро, во втором нужно дробь разложить на суму элементарных дробей
При сведении к общему знаменателю получим такие числительные
Далее раскрываем скобки и группируем
Приравниваем значение при одинаковых степенях "икс" справа и слева. В результате придем к системе трех линейных уравнений (СЛАУ) с тремя неизвестными.
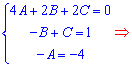
Как решать системы уравнений описано в других статьях сайта. В конечном варианте Вы получите следующее решения СЛАУ
A=4; B=-9/2; C=-7/2.
Подставляем постоянные в разложение дроби на простейшие и выполняем интегрирование
На этом пример решен.
Пример 16. Опять нужно найти интеграл от дробно-рациональной функции. Для начала кубическое уравнение, которое содержится в знаменателе дроби разложим на простые множители
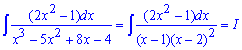
Далее выполняем разложение дроби на простейшие
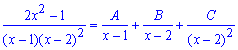
Сводим правую сторону к общему знаменателю и раскрываем скобки в числителе.
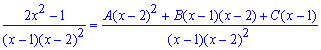
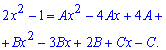
Приравниваем коэффициенты при одинаковых степенях переменной. Снова придем к СЛАУ с тремя неизвестными
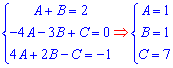
Подставляем значения А,В,С в разложение и вычисляем интеграл
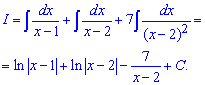
Первые два слагаемых дают логарифм, последний тоже легко найти.
Пример 17. В знаменателе дробно-рациональной функции имеем разницу кубов. Ее по формулам сокращенного умножения раскладываем на два простых множителя
Далее полученную дробную функцию расписываем на сумму простых дробей и сводим их под общий знаменатель
В числителе получим следующее выражение.
Из него формируем систему линейных уравнений для вычисления 3 неизвестных
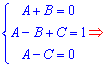
A=1/3; B=-1/3; C=1/3.
Подставляем А, В, С в формулу и выполняем интегрирование. В результате придем к такому ответу
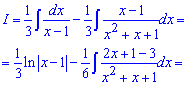
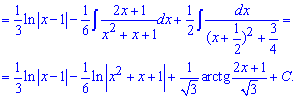
Здесь числитель второго интеграла превращали в логарифм, при этом остаток под интегралом дает арктангенс.
Подобных примеров на интегрирование рациональных дробей в интернете очень много. Похожие примеры Вы можете найти из приведенных ниже материалов.
Готовые решения контрольной по интегрированию
]]>Интегрирование тригонометрических функций
Пример 20. Для вычисления интеграла от произведения косинуса и синуса необходимо синус внести под дифференциал. В результате перейдем к интегрированию показательной функции от косинуса. Через формулы это будет выглядеть следующим образом
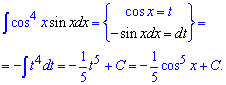
Пример 21. Для начала следует проанализировать аргументы под синусом и косинусом и показатели. Произведение функций можем записать через квадрат синуса двойного угла, который в свою очередь записываем через косинус в два раза большего аргумента. Как только дойдем до функций в первой степени имеем право применять табличные интегралы
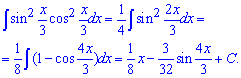
Пример 22. Косинус двойного угла записываем по тригонометрическим формулам через косинус 1 угла. Далее чтобы получить интеграл от одной из тригонометрических функций необходимо синус внести под дифференциал. Дальнейшие вычисления сводятся к интегрированию простых функций
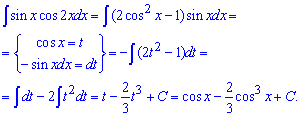
Следует отметить что в этом и предыдущем примере использовали некоторые тригонометрические формулы. Для вычисления всех возможных интегралов их нужно знать или иметь под рукой очень много, но для решения базовых интегралов необходимо не более 10 популярных тригонометрических формул.
Пример 23. Имеем дробную тригонометрическую функцию. Для ее вычисления необходимо применить универсальную тригонометрическую замену – тангенс половины угла. Синус через тангенс половины угла выражается зависимостью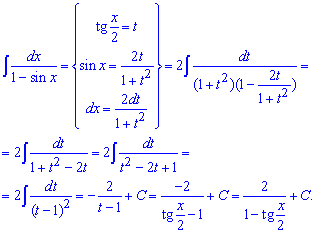
После подстановки замены в интеграл и упрощении, которое зачастую при таких заменах бывает не простым, получим простую дробную функцию. Ее интегрировать должен уметь каждый студент. Если нет, то контрольная или самостоятельная на интегралы покажет "кто есть кто".
Пример 24. Чтобы найти интеграл можно применить универсальную тригонометрическую замену, как один из распространенных способов. Как альтернативный вариант можно вынести квадрат косинуса за скобки, а в скобках добавить и вычесть единицу, чтобы получить тангенс. Далее его обозначаем за новую переменную и вычисляем дифференциал (он совпадет со второй частью подынтегральной функции). Таким образом перейдем к интегрированию функции, которая сводится к арктангенсу.
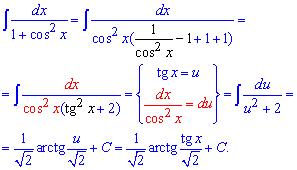
Такой подход несколько упрощает вычисления, но не всегда легко его увидеть и применить. Выполните интегрирование приведенной функции через универсальную замену переменных самостоятельно.
Пример 25. Интеграл от котангенса в квадрате от тройного аргумента находим после следующих преобразований
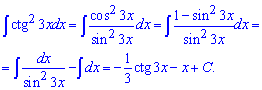
Здесь использована простая зависимость, что сумма квадратов синуса и косинуса равна единице.
Остальные готовых ответы из контрольной работы на интегралы Вы найдете по приведенным ниже ссылкам. Задания и схемы их вычислений помогут разобраться практически с любыми интегралами.
Готовые решения контрольных с интегрирования
]]>
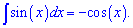Те кто изучает первоначальную должны помнить что к правой стороне следует добавить постоянную 
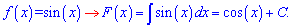Ету постоянную определяют с дополнительной условия.График синуса имеет вид
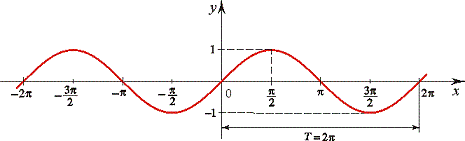
Синус нечетная, а косинус - четная функция, поэтому при интегрировании появляется знак минус. В начале всем кажется все простым и понятным. Но рано или поздно наступает время усложнять интеграл, то есть интегрировать синус двойного угла, тройного аргумента и т.д. И во многих возникают трудности с интегрированием. Для вывода формулы интеграла для sin (k*x) проведем все выкладки сначала. Для того чтобы свести интеграл к табличной формулы надо внести коэффициент под дифференциал, но это изменит сам интеграл. Поэтому одновременно делим на коэффициент
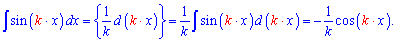
Зная эту формулу, интеграл от синуса двойного угла записываем одной строкой
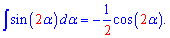Далее можем проинтегрировать синус тройного угла
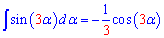и т.д.
int(sin(k*x)=-1/k*cos(k*x).
По такой же формуле выводят интеграл от синуса половины угла, который равен минус 2 косинус половины угла.
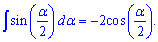Интеграл от синуса одной третьей х равен
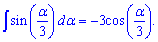
Распространенные примеры интегрирования синуса
Пример 1. Найти интеграл от sin(4*x).
Решение: По формуле интегрирования находим
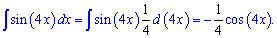
Пример 2. Вычислить интеграл от sin(5*x).
Решение: Выполняем интегрирования
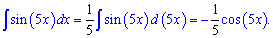
Пример 3. Проинтегрировать выражение sin(7*x).
Решение: Находим неопределенный интеграл
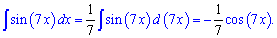
Пример 4. Найти интеграл функции y=sin(x/5).
Решение: Находим неопределенный интеграл
Как только Вы научитесь вычислять простые интегралы от синуса можете переходить к определенному интегралу
Пример 5. Найти первоначальную от sin(x) которая в нуле равна 2.
Решение: Вычисляем первоначальную
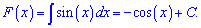
Из условия на первоначальную находим постоянную
-cos(0)+C=2;
C=2+cos(0)=3.
Возвращаемся к первоначальной и подставляем найденную постоянную
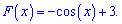
Это и есть ответ к задаче.
Пример 7. Проинтегрировать синус двойного угла y=sin(2*x) от 0 до 45 градусов.
Решение: Записываем интеграл от синуса и подставляем пределы интегрирования
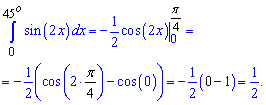
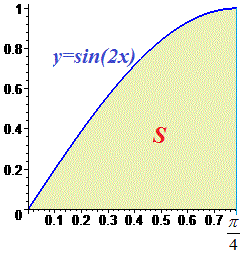
По физическому содержанию определенный интеграл равен площади фигуры ограниченной функцией sin (x) и осью абсцисс.
Но определенный интеграл и площадь, это не одно и то же. Интеграл может быть отрицательным, а площадь нет. Если функция большую площадь имеет под осью абсцисс, то ее определенный интеграл отрицательный.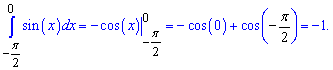
Площадь криволинейной трапеции равна интегралу от разницы уравнения верхней кривой и нижней.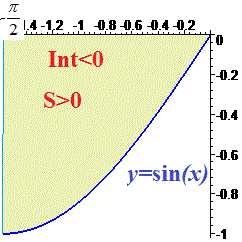
В данном случае верхняя кривая это ось абсцисс или y = 0. Нижняя - это график синуса. Поэтому формула площади синус функции равна 1, или определенному интегралу по модулю.
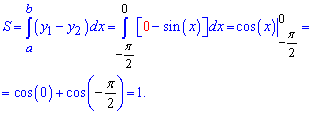
Если функция антисимметрична относительно оси абсцисс то ее интеграл равен нулю, а площадь равна двойному интегралу графика над осью абсцисс. Например, интеграл синуса двойного угла от -45 до 45 градусов равен нулю
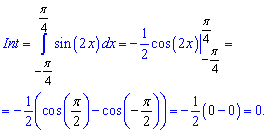
В то же время площадь заштрихованной фигуры равна единице.
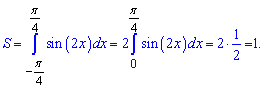
На графике это будет выглядеть.
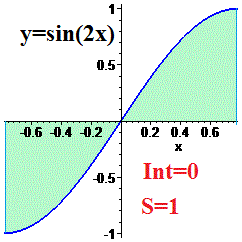
Из следующих материалов Вы узнаете, как найти интеграл от функции вида
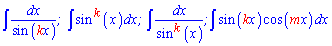какие формулы свертки и замены переменных при этом следует использовать. Также Вы овладеете методикой вычисления интегралов вида полином умноженый на синус функцию
где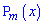 
- полином от переменной. В таких случаях применяют интегрирования по частям, но об этом пойдет речь позже.
На этом знакомство с интегрированием синуса завершается. Интегралы от других тригонометрических и обратных к ним функций Вы найдете на страницах категории "Интегрирование функций".
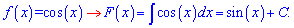Постоянную определяют с дополнительного условия на первоначальную.График косинуса имеет вид
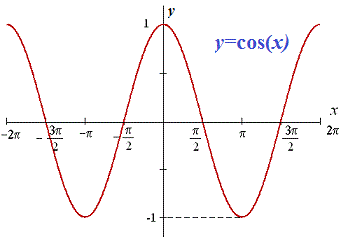Само по себе определение интеграла косинуса достаточно простое. Но как только задают вычислить интеграл косинуса двойного угла, тройного или половины угла, сразу возникают трудности в половины студентов. Выведем формулу интегрирования для функции cos (k*x). Для применения табличной формулы интегрирования надо внести коэффициент под дифференциал, что может привести к изменению самого интеграл. Поэтому одновременно необходимо разделить на этот коэффициент.
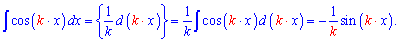. Зная приведенную формулу, проинтегрировать косинус двойного угла сможет каждый школьник 10, 11 класса. Все что необходимо это подставить 2 или 3 в интеграл
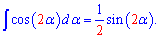
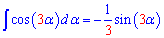и по индукции следующие интегралыint(sin(k*x)=-1/k*cos(k*x).
Приведенная формула позволяет вычислить интеграл от косинуса половины угла
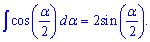и интеграл от косинуса одной трети угла
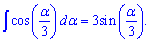В этих случаях коэффициент, стоящий при переменной в косинусе при интегрировании становится обратным значением перед синусом.
Распространенные примеры интегрирования косинуса
Пример 1. Найти интеграл от cos(5*x).
Решение: По формуле интегрируем косинус
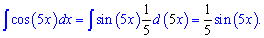
Пример 2. Вычислить интеграл от cos(7*x).
Решение: Выполняем интегрирование
Пример 3. Проинтегрировать выражение cos (11*x).
Решение: Вычисляем неопределенный интеграл
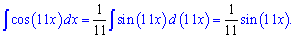
Пример 4. Найти интеграл функции y= cos (x/5).
Решение: Записываем неопределенный интеграл
Пример 5. Найти интеграл функции y= cos (x/6).
Решение: Проинтегрируем по приведенной выше формуле
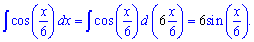Как только Вы освоите методику интегрирования на простых примерах, смело можете переходить к определенным интегралам и первообразным. Для отискания определенного интеграла проводим интегрирование, а дальше подставляем пределы интегрирования и находим изменение первообразной функции.
Пример 6. Проинтегрировать косинус двойного угла y = cos (2 * x) от 0 до 45 градусов.
Решение: Находим указанный интеграл от косинуса
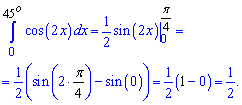
Пример 7. Найти интеграл от косинуса y = cos (x) от 0 до 60 градусов.
Решение: Вычисляем интеграл и подставляем пределы интегрирования
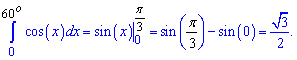
Пример 8. Найти первоначальную от cos (x), которая при 30 градусах равна 1.
Решение: Находим первоначальную
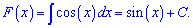С наложенного условия на первоначальную вычисляем постоянную
sin(Pi/6)+C=1; C=1-
sin(Pi/6)=1-0,5=0,5.
Подставляем полученную постоянную в уравнение
На этом задача решена. На таких простых примерах Вы четко должны знать, чему равный интеграл от косинуса.
Далее полученные знания можно применять для вычисления площадей криволинейных трапеций. Это достаточно абстрактное понятие, но с помощью интегрирования находить площадь фигур достаточно просто и быстро. Следует только помнить, что площадь всегда принимает положительное значение, в то время как определенный интеграл может принимать отрицательное значение.
Например вычислим площадь и интеграл от косинуса, если переменная принадлежит интервалу от 0 до 2*Pi.
По физическому содержанию площадь равна заштрихованным поверхностям.
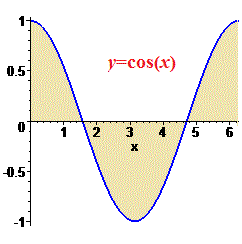Находим определенный интеграл в указанных пределах
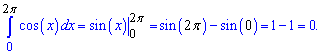Он равен нулю. Что касается площади, то сначала следует найти точки пересечения с осью абсцисс на этом интервале
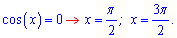Таким образом площадь необходимо искать на трех промежутках
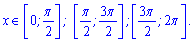Ось абсцисс можем записать функцией y = 0. Таким образом на первом промежутке площадь равна интегралу от косинуса,
на втором 0-cos (x) = - cos (x) от минус косинуса и на третьем от косинуса. Все при вычислении площади зависит от того, какая функция принимает большее значение по оси ординат (Oy). Вычисляем площадь интегрированием в указаных пределах
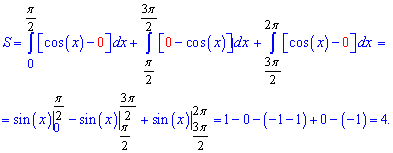Таким образом искомая площадь равна 4. Если иметь график функции перед глазами, то данное значение можно получить как 4 площади косинус функции, которые периодически повторяются
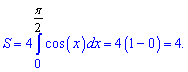На этом знакомство с интегрированием косинуса завершается. Приведенная методика интегрирования позволяет вычислить 80% основных задач на интегрирование косинуса. Остальные 20% Вы научитесь после изучения способов нахождения интегралов от функций вида
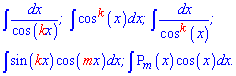Мы научим Вас, какие свертки и замены переменных следует использовать, в каких случаях целесообразно интегрировать по частям.
Интегралы от других тригонометрических и обратных к ним функций Вы найдете в категории "Интегрирование функций".
Начнем с тангенса, распишем его в виде частки синуса на косинус
tg(x)=sin(x)/cos(x)
и подставим в интеграл.
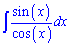Сейчас Вам понятно. Далее нужно внести синус под дифференциал, чтобы свести интеграции в логарифма
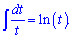В результате получим
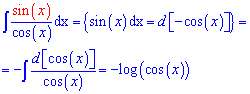Таким образом вывели простую и нужную на практике формулу - интеграл от тангенса равен логарифму косинуса со знаком минус. Int(tan(x),x)=-log(cos(x)).
По приведенной схеме выведем формулу для интеграла от котангенса. Записываем частку косинуса на синус в интеграл и после внесения косинуса под дифференциал сводим интеграл к логарифму
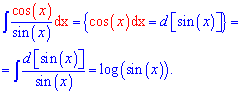Интеграл от котангенса равный логарифму от синуса. Int(cot(x),x)=log(sin(x)).
Простые на вид формулы интегралов от тангенса и котангенса позволяют решить немало сложных примеров, например интегрирования тангенса двойного угла или котангенса половины угла.
Примеры интегрирования тангенса и котангенса
Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса
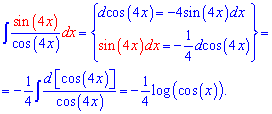
Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интегралаtan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5.
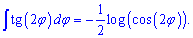Для тангенса половины угла tan (phi / 2) интеграл равен -2 умножить на логарифм косинуса половины угла
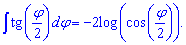По индукции получим формулу интеграла для тангенса одной третьей угла tan(phi/3)
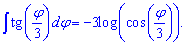
Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал
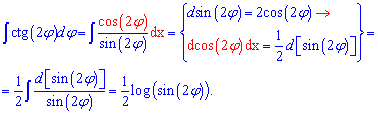
Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
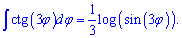Интегралы от котангенса половины и трети угла будут иметь множителями перед логарифмом соответственно двойку и тройку
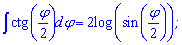
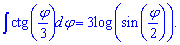При нахождении первоначальной от тангенса и котангенса следует справа добавить постоянную
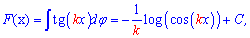
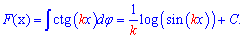Зная данную методику, Вы знаете как найти интеграл от тангенса, аргумент которого содержит множителем произвольное число.
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.
С методикой интегрирования обратных тригонометрических функций, иррациональных и показательных Вы можете ознакомиться на страницах категории "Интегрирование функции" в левом меню сайта.