Контрольную работу на интегрирование функций, в том числе и рациональных дробей задают студентам 1, 2 курсов. Примеры интегралов в основном будут интересны для математиков, экономистов, статистов. Данные примеры задавали на контрольной работе в ЛНУ им. И. Франка. Условия следующих примеров "Найти интеграл" или "Вычислить интеграл", поэтому для экономии места и Вашего времени их не выписывали.
Пример 15. Мы пришли к интегрированию дробно-рациональных функций. Они занимают особое место среди интегралов, поскольку требуют много времени на вычисление и помогают преподавателям проверить Ваши знания не только по интегрированию. Для упрощения функции под интегралом добавим и вычтем в числителе выражение, которое позволит разбить функцию под интегралом на две простые
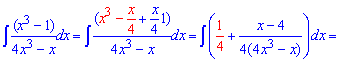
![]()
В результате один интеграл находим довольно быстро, во втором нужно дробь разложить на суму элементарных дробей
![]()
При сведении к общему знаменателю получим такие числительные
![]()
Далее раскрываем скобки и группируем
![]()
Приравниваем значение при одинаковых степенях "икс" справа и слева. В результате придем к системе трех линейных уравнений (СЛАУ) с тремя неизвестными.
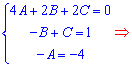
Как решать системы уравнений описано в других статьях сайта. В конечном варианте Вы получите следующее решения СЛАУ
A=4; B=-9/2; C=-7/2.
Подставляем постоянные в разложение дроби на простейшие и выполняем интегрирование
![]()
![]()
На этом пример решен.
Пример 16. Опять нужно найти интеграл от дробно-рациональной функции. Для начала кубическое уравнение, которое содержится в знаменателе дроби разложим на простые множители
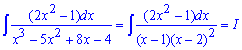
Далее выполняем разложение дроби на простейшие
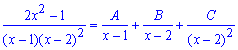
Сводим правую сторону к общему знаменателю и раскрываем скобки в числителе.
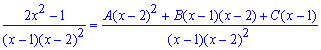
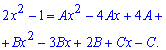
Приравниваем коэффициенты при одинаковых степенях переменной. Снова придем к СЛАУ с тремя неизвестными
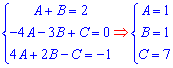
Подставляем значения А,В,С в разложение и вычисляем интеграл
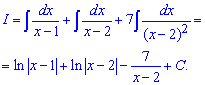
Первые два слагаемых дают логарифм, последний тоже легко найти.
Пример 17. В знаменателе дробно-рациональной функции имеем разницу кубов. Ее по формулам сокращенного умножения раскладываем на два простых множителя
![]()
Далее полученную дробную функцию расписываем на сумму простых дробей и сводим их под общий знаменатель
![]()
В числителе получим следующее выражение.
![]()
Из него формируем систему линейных уравнений для вычисления 3 неизвестных
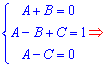
A=1/3; B=-1/3; C=1/3.
Подставляем А, В, С в формулу и выполняем интегрирование. В результате придем к такому ответу
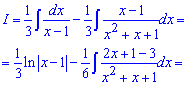
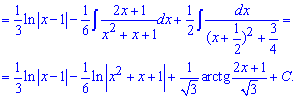
Здесь числитель второго интеграла превращали в логарифм, при этом остаток под интегралом дает арктангенс.
Подобных примеров на интегрирование рациональных дробей в интернете очень много. Похожие примеры Вы можете найти из приведенных ниже материалов.
Готовые решения контрольной по интегрированию


