Примеры интегрирования по частям подобного состава задают студентам 1, 2 курсов. Данные задания задавали на контрольной работе в ЛНУ им. И. Франка. Чтобы формулы в задачах и ответах не повторялись же задачи описывать не будем. По условию заданий нужно или "Найти интеграл", или "Вычислить интеграл".
Пример 8. Интеграл находим по правилу интегрирования частями int(u*dv)=u*v-int(v*du). Здесь главное правильно выбрать функции под правило. (Для себя запомните что за dv если возможно выбирают периодические функции или такие, которые при дифференцировании с точностью до множителя дают сами себя - экспонента). В этом интеграле нужно синус внести под дифференциал
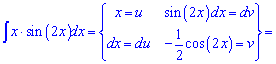
Дальнейшее интегрирование достаточно простое и на деталях останавливаться не будем.
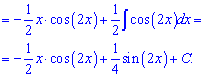
Пример 9.Снова нужно применять правило интегрирования по частям u*dv. Здесь имеем произведение периодической функции на экспоненту, поэтому что лучше вносить под дифференциал выбирать Вам. Можно как экспоненту, так и косинус (в каждом варианте получим рекуррентную формулу).
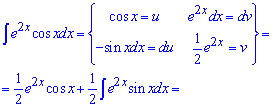
Применяем интегрирование по частям повторно
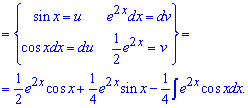
Пришли к рекуррентной формуле. Если записать интеграл который искали и результат вычислений то получим два подобные слагаемые
![]()
Группируем их и находим искомый интеграл
![]()
![]()
Пример 10. Имеем готовую запись интеграла под правило u*dv. Находим du и выполняем интегрирование
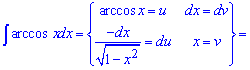
![]()
Сводим второй интеграл под табличную формулу и вычисляем его
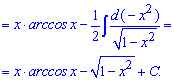
Пример 11. Обозначим за новую переменную cos(ln(x))=u і найдем du, затем внесением под дифференциал
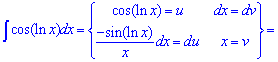
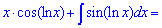
К интегралу повторно применяем правило интегрирования по частям
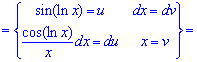

Пришли к рекуррентной формуле
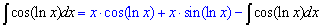
с которой и вычисляем неизвестный интеграл
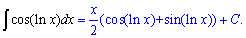
Пример 12. Для нахождения интеграла выделим в знаменателе полный квадрат. Далее сведя знаменатель к известной формуле интегрирования получим арктангенс
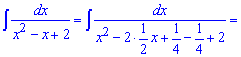
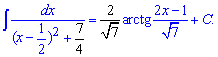
Хорошо запомните порядок чередования множителей. Единица разделена на корень из свободного члена фигурирует перед арктангенсом, также этот множитель присутствует в арктангенс перед переменной.
Пример 13. Дело имеем с подобным интегралом, только в знаменателе квадратичная зависимость находится под корнем. Выделяем полный квадрат и сводим под формулу интегрирования, которая дает логарифм
![]()
![]()
Вот такие бывают примеры на контрольной или тестах. Хорошо запомните основные схемы интегрирования.
Если не можете решить интеграл сами, тогда обращайтесь за помощью.
Готовые решения контрольной по интегрированию


