ЗНО 2015 математика. Система рівнянь з параметром

Шановні школярі, випускники, абітурієнти, цей розділ допоможе при підготовці до зовнішнього оцінювання 2017 року з математики. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці до тестування, систематизувати та підвищити накопичений рівень знань з математики.

Розділ II. Рівняння і нерівності

Завдання 11.58 Знайдіть значення параметра а, при якому система рівнянь

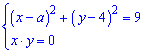
має єдиний розв'язок. Якщо таких значень параметра а кілька, то запишіть їх добуток.
Розв'язання: Почнемо з аналізу рівнянь, які входять в систему. Перше рівняння описує коло радіусом 3 із зміщеним від початку координат центром. Друге рівняння розв'язком має прямі

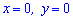
що співпадають з координатними осями. Оскільки коло по осі Оy зміщене на чотири, а його радіус рівний 3 то воно не має точок перетину з віссю абсцис (Ох) (див. рис.). Залишається знайти точки перетину з віссю ординат.

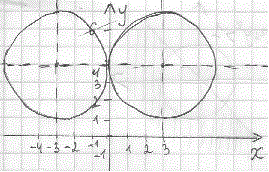
В такому випадку в перше рівняння слід підставити y=4; x=0 і знайти параметр

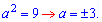
За умовою знаходимо добуток параметрів
(-3)*3=-9.
Відповідь: -9.

Завдання 11.59 (Т-06, 13) Знайдіть НАЙМЕНШЕ значення параметра а, при якому система рівнянь

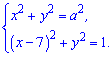
має єдиний розв'язок.
Розв'язання: Проаналізуємо рівняння, які входять в систему рівнянь. Обидва описують рівняння кола, перше з центром в початку координат і радіусом а, друге – з центром зміщеним по осі абсцис на 7 одиниць праворуч і радіусом 1. Таким чином друге графік другої функції перетинає вісь абсцис в точках
7-1=6; 7+1=8.
Щоб перше коло з другом мало точки дотику необхідно, щоб вони дотикалися в знайдених точках.

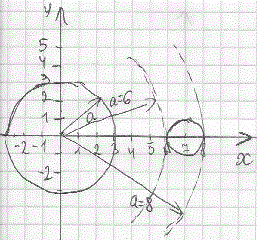
Звідси параметр а приймає значення 6 або 8.
Але це ще не кінець аналізу системи рівнянь. Оскільки в рівнянні параметр стоїть в парному степені, то він може приймати і від'ємне значення, тобто -6 і -8 також задовільнятимуть рівняння.
І тільки тепер маємо право вписати потрібний варіант параметра (-8).
Відповідь: -8.