Центр поверхні другого порядку. Заміна системи координат

Завдання на перенесення початку координат вимагають знань всього попереднього матеріалу, тому якщо Ви почали читати цю статтю і багато чого не розумієте, тоді реомендуємо ознайомитися з попередніми публікаціями. Тут Вам також стануть в нагоді знання систем координат, а саме як правильно виконати паралельний перенос. Проанізуйте відповіді і навчіться обчислювати завдання на переніс центру поверхні.

Задача 6.3.2 б) Перенесіть початок координат в центр поверхні другого порядку:
y²+3xy+xz+2yz+3x+2y=0;
Розв'язання: Цей та наступні приклади дозволять Вам самостійно опанувати методику знаходження центру поверхні.
Спершу виписуємо коефіцієнти рівняння заданої поверхні другого порядку:
a₁₁=0, a₂₂=1, a₃₃=0, a₁₂=1.5, a₁₃=0.5, a₂₃=1, a₁₄=1.5, a₂₄=1, a₃₄=0, a₄₄=0.
Як правильно виписати оефіцієнти описано в попередніх публікаціях.
Будуємо систему рівнянь та методом Гауса зводимо її до східчастої: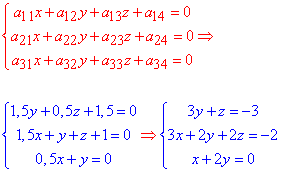
Звідси отримаємо центр поверхні другого порядку

Перенесемо початок координат в центр O(0,8; -0,4;-1,8), необхідна заміна координат наступна

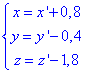
Звідси нові координати в старій системі

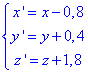
Підставляємо їх в рівняння поверхні та знаходимо шукану відповідь

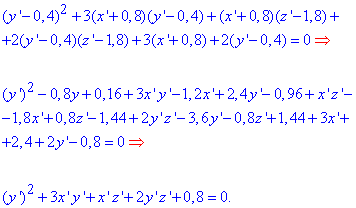
Хід трансформації рівняння поверхні до нових координат можете прослідкувати з аналізу наведених формул.

Задача в) Перенесіть початок координат в центр поверхні другого порядку: x²+2y²2-z²+2x-4y+2z+1=0.

Розв'язання: Дотримуємося наведеної інструкції і з практикою, що раз швидше зможете виконувати подібні вправи.
З рівняння поверхні виписуємо коефіцієнти при змінних:
a₁₁=10, a₂₂=2, a₃₃=-1, a₁₂=0, a₁₃=0, a₂₃=0, a₁₄=15, a₂₄=-2, a₃₄=1, a₄₄=1.
Правильно виписані значення - це половина правиьної відповіді, тому, якщо Вам тяжко зрозуміти звідки їх беремо, оді краще застосовуйте формули часткових похідних по змінних.
І в першому, і в другому випадку Ви прийдете до системи трьох рівнянь з трьома невідомии:

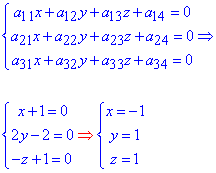
Як її обчислювати залежить від Ваших вподобань, проте в більшості випадків сам запис СЛАР підкаже, що далі з ними робити.
В цьому завданні система проста, тому легко знаходимо центр поверхні -O(-1;1;1).
Далі виписуємо заміну координат, яка перенесе початок координат в центр поверхні - точку O:

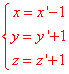
Звідси перехід від нових координат до попередніх має вигляд

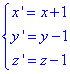
Підставляємо заміну змінних та розписуємо рівняння поверхні в якої центр співпадає з початком координат

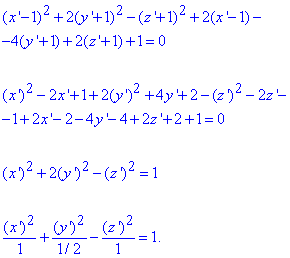
Отримали канонічне рівняння однополого гіперболоїда (поверхня обертання).
Думаю, що більшість наведених прикладів допоможуть Вам вправніше вирішувати практичні завдання, не мати страху на екзаменах та контроьних.