ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 90.Розв'яжіть логарифмічне рівняння:
1) 
Розв'язання:
Функція визначена для всіх невідомих більших за нуль. Перетворимо рівняння ввівши нову змінну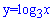 
. Отримаємо квадратне рівняння з відповідними коренями
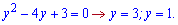
Повертаємося до заміни і знаходимо невідому
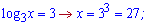
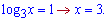
Логарифмічне рівняння має два розв'язки x=27;x=3.
2) 
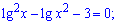
Розв'язання:
Використовуємо схему розв'язування попереднього завдання.
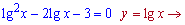
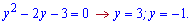
Згадуємо заміну і знаходимо невідомий розв'язок
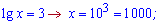
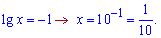
Із заміною обчислення виконуються набагато швидше та зрозуміліше, тому її слід виконувати всюди де це можливо.
3) 
Розв'язання:
Зводимо логарифмічне рівняння до квадратного
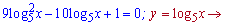
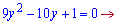
Теорема Вієта тут не допоможе, тому знаходимо дискримінант
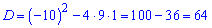
та корені рівняння
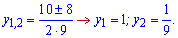
Підставляємо знайдені значення в заміну та обчислюємо корені
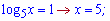
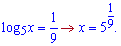
Ось так просто отримали відповідь.
4) 
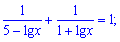
Розв'язання:
Жодних перетворень виконувати не потрібно, вводимо заміну 
та розв'язуємо відносно неї
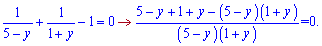
Знаменник не повинен дорівнювати нулю
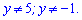
Чисельник після розкриття дужок та групування подібних доданків набуде вигляду квадратного рівняння
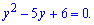
Корені за теоремою Вієта рівні y=2; y=3.
Повертаємося до заміни і обчислюємо
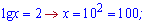
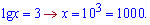
Отже 100, 100 - розв'язки логарифмічного рівняння.
5) 
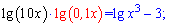
Розв'язання:
Такі приклади достатньо специфічні в обчисленнях.
Основа в них однакова, однак функції різняться.
Для того, щоб звести до квадратного рівняння потрібно розписати логарифми через доданки (використавши властивість логарифма)
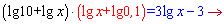
Вводимо заміну 
і спрощуємо
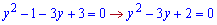
Корені рівняння рівні y=1; y=2.
Повертаємося до заміни і знаходимо розв'язок логарифмічного рівняння
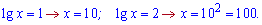
Значення 10 та 100 будуть єдиними.
6) 
Розв'язання:
На вигляд складне рівняння при знанні властивостей логарифма досить швидко вирішується. Вносимо все під один логарифм та вводимо заміну змінних
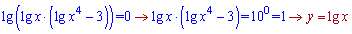
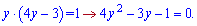
Областю визначення буде множина
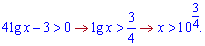
Дискримінант рівний
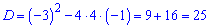
корені рівняння
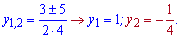
Другий корінь відкидаємо через обмеження на логарифм, перший дає наступний вклад
7) 
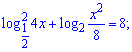
Розв'язання:
Завдання на перевірку знань властивостей логарифма. Перетворимо ліву частину рівняння
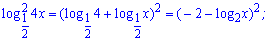
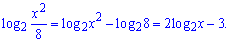
Думаю, що правила на основі яких виконали перетворення Ви знаєте.
Підставляємо в рівняння
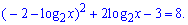
Заміна 
перетворить логарифмічне рівняння на квадратне
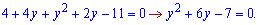
Корені рівні y=-7; y=1.
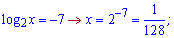
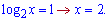
8) 
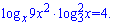
Розв'язання:
Перший множник розписуємо як суму логарифмів
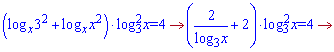
та зводимо до квадратного рівняння
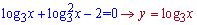
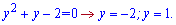
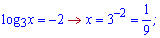
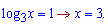
На цьому розрахунки завершилися, інші приклади можете розглянути в наступних статтях.
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Логарифмічні рівняння. №89
- Наступні відповіді - Логарифмічні рівняння. №91
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
