Продолжаем разбирать готовые ответы на правило Лопиталя и сегодня рассмотрим примеры сведение неопределенностей 1^∞, 0^0, 0^∞ под это правило. Все случаи рассмотреть невозможно, однако 15 примеров, что идут далее помогут разобраться с алгоритмами вычисления пределов каждого внимательного студента.
Метод логарифмирования раскрытия неопределенностей в пределах
Пример 16 Вычислить предел по формуле Лопиталя limit(x^(1/(1-x)),x→0)
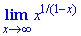
Решение: Предел имеет особенность типа 1^∞. Для применения метода логарифмирования за новую функцию обозначим y=x1/(1-x). Делее логарифмируем обе части, получим
ln(y)=ln(x1/(1-x))=ln(x)/(1-x).
По правилу Лопиталя раскрываем неопределенность вида 0/0
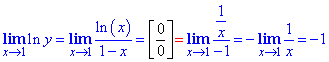
Это еще не конечный ответ, чтобы найти y нужно экспоненту поднести к степени равному найденному пределу.
ln(y)=-1 →y=e-1=1/e.
Пример 17 Раскрыть неопределенность по правилу Лопиталя

Решение: Имеем неопределенность типа ноль в степени ноль 0^0. Поступаем по схеме для показательных функций, а именно – логарифмуємо выражение в лимите.
y=(arcsin(x))2;
ln(y)=2x•ln(arcsin(x)).
Для раскрытия неопределенности используем правило Лопиталя дважды
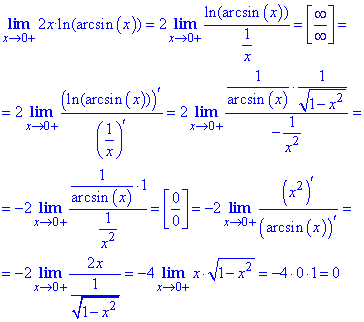
Здесь нужно брать производную от ln(arcsin(x)), как от сложной функции, помните об этом.
Пример 18 Найти предел пользуясь правилом Лопиталя
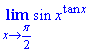
Решение: Подставки аргумента равного 90 градусам дает неопределенность вида единицы в степени бесконечность 1^∞. Согласно алгоритму вычисления пределов, функцию под лимитом следует прологарифмирувать. Далее найти предел логарифма, а потом экспонента в степени полученного значения и будет ответом к заданию. Проведем вычисления
y= tan(x)sin(x);
ln(y)=ln(sin(x))^tg(x)=tan(x)•ln(sin(x)).
Воспользуемся правилом Лопиталя, предварительно заменив тангенс на котангенс по формуле tg(x)=1/cot(x).
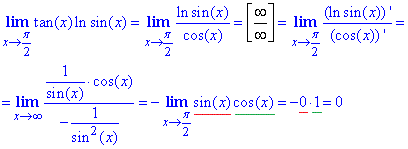
Но это еще не ответ, нужно потенцировать 0.
ln(y)=0 →y=e0=e.
Сведение неопределенностей в пределах под правило Лопиталя
Пример 19 Мнимая подстановка x=2 в функцию дает неопределенность вида 0/0, поэтому применяем правило Лопиталя однократно, а далее без труда вычисляем лимит.
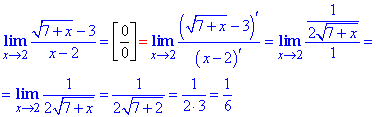
Пример 20 Подстановкой убеждаемся, что имеем неопределенность вида 0/0. По формуле Лопиталя вычисляем производную числителя и знаменателя по переменной, чтобы раскрыть неопределенность.
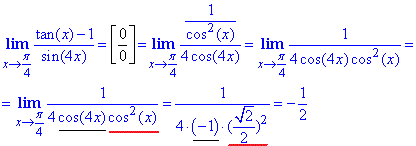
Пример 21 Имеем долю полиномов без свободного члена, что в предельной точке дает особенность вида 0/0. Для ее раскрытие по правилу Лопиталя дифференцируем каждый полином пока не получим дробь, предел которой можно вычислить подстановкой
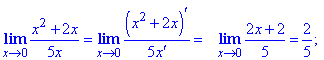
Пример 22 В числителе имеем x^2, в знаменателе 2^x.
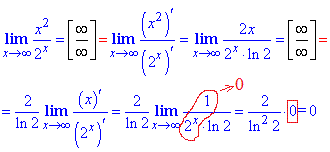
Решение: Поскольку аргумент стремится к бесконечности, то прямая подстановка дает особенность вида ∞/∞. Ее раскрываем дважды беря производные числителя и знаменателя по "x".
Пример 23 Имеем дробь с функций e^x, x^a. В такого сорта примерах правило Лопиталя применяют до тех пор, пока в знаменателе не получим факториал числа a!
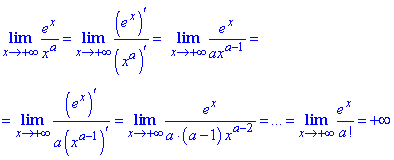
Запомните, что ограничений на количество повторных применений правила Лопиталя нет, находим производные до тех пор, пока имеем одну из неопределенностей 0/0 или ∞/∞.
Пример 24 Очередное задание на раскрытие неопределенности вида ∞/∞ решаем путем дифференцирования отдельно числителя x^a и знаменателя ln(x).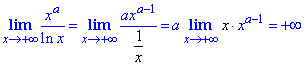
Пример 25 Имеем долю функций f(x)=arctan(x) и g(x)=e3x-1. В нуле они дают неопределенность вида 0/0, поэтому имеем все основания применить правило Лопиталя.
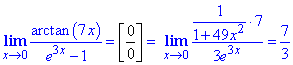
Поскольку выражения e^3x→1 и 1/(1+49x^2) →1 когда x→0, то предел равен 7/3.
Пример 26 Согласно алгоритму, чтобы раскрыть неопределенность ∞/∞ дважды применяем правило Лопиталя.
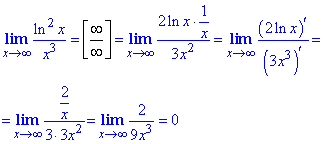
Пример 27 Переходим от неопределенности вида ноль умножить на бесконечность к неопределенности бесконечность разделить на бесконечность, которую раскрываем по правилу Лопиталя через дифференцирование числителя и знаменателя дроби. Внимательно посмотрите схему перехода от одной неопределенности к другой и запомните, что когда имеем произведение логарифма на другую функцию, то в знаменатель переносим последнюю, а не логарифм.
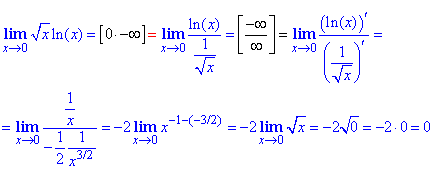
Пример 28 Прямая подстановка дает неопределенность ноль умножить на бесконечность 0*∞
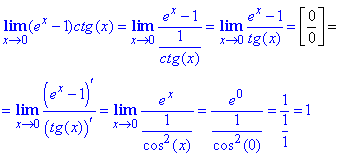
Чтобы свести пример к применению правила Лопиталя в искусственный способ котангенс переносим в знаменатель дроби, а далее заменяем 1/ctg(x)=tg(x). Таким образом получаем особенность в виде доли бесконечно малых функций, раскрываем дифференцированием по Лопиталю и подстановкой x=0.
Раскрытие неопределенностей ∞-∞
Пределы с неопределенностью ∞-∞ также раскрываем по правилу Лопиталя, но предварительно проводим определенные элементарные действия над слагаемыми, чтобы перейти от разности бесконечно больших функций к дроби.
Пример 29 Формулы ниже хорошо иллюстрируют как дважды применяли дифференцирование числителя и знаменателя дроби, чтобы избавиться от неопределенности 0/0.
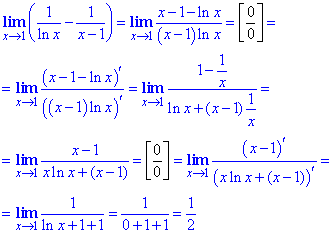
Пример 30 Имеем неопределенность вида ∞-∞, которую раскрываем путем сведения дробей к общему знаменателю. Далее по правилу Лопиталя вычисляем производные числителя и знаменателя, и так дважды.
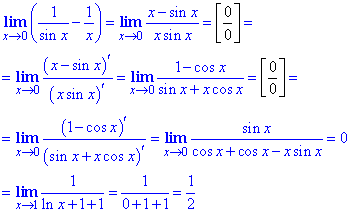
И только когда избавляемся неопределенности выполняем подстановку аргумента в предел. Считаем, чтобы начать решать примеры на правило Лопиталя, 30 приведенных примеров вполне достаточно. Если есть проблемы с расчетными или модулями, то всегда можете обращаться к нам за помощью!


