Решения задач внешнего тестирования по математике пригодятся Вам при подготовке к тестированию. Ответы на задания 17-22 второй сесии 2013 не слишком сложные и после анализа Вами внесут существенный вклад в подготовку к ВНО.
------------------------------
Задача 17. Упростите выражение
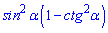
Варианты ответов:
А)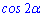 
Б)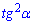 
В) 1
Г)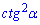 
Д)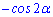 
Решение : Преобразуем выражение в скобках
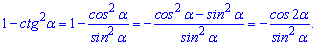
и упростим
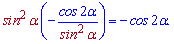
Без знания преобразований тригонометрических выражений подобные задачи не всегда легко удается решить поэтому постарайтесь при подготовке к ВНО или иного тестирования изучить хотя бы базовые преобразования.
Ответ: Д.
------------------------------
Задача 18. Найдите производную функции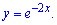 
Варианты ответов:
А)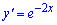 
Б)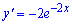 
В)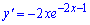 
Г)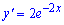 
Д)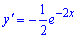 
Решение: По правилу дифференцирования сложной функции находим
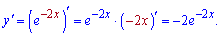
Ответ: Б.
------------------------------
Задача 19. Решите неравенство
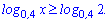
Варианты ответов:
А)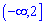 
Б) 
В)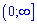 
Г)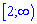 
Д)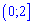 
Решение: Поскольку основы одинаковы то экспонируем обе части неравенства, помня при этом важное правило: если в логарифмическом неравенстве основа меньше единицы то знак неравенства меняется на противоположный
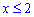
Так как ОДЗ логарифма начинается от нуля и при отрицательных значениях он не существует то решением будет промежуток
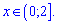
Ответь: Д.
------------------------------
Задача 20. Для разогрева в микроволновой печи жидких блюд используют сосуд в форме цилиндра, радиус основания которого равен 9 см. Сосуд ставится на горизонтальный диск в форме круга и накрывается крышкой имеющей форму полусферы (см. рисунок). Радиус полусферы равен 12 см и меньше радиуса круга. Укажите самое больше из приведенных значений которому может равняться высота сосуда если он не касается крышки.
Варианты ответов:
А) 3 см
Б) 5 см
В) 6 см
Г) 7 см
Д) 8 см
Решение: Задача достаточно каверзна и многие из Вас ее не решали . Высоту сосуда можно найти применив теорему Пифагора к прямоугольному треугольнику с гипотенузой, которая равна радиусу полусферы и катетами, которые равны высоте и радиусу основания сосуда.
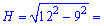
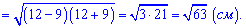
Ближайшее целое значение находим из следующих соображений
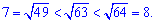
Таким образом, если сосуд не касается крышки то его максимальная высота равна 7 см.
Ответ: Г.
------------------------------
Задача 21. Из пунктов А и В одновременно по шоссе навстречу друг другу выехали два велосипедиста. Они ехали без остановок с постоянными скоростями: первый - со скоростью х км/ч, второй - со скоростью у км/ч (x>y). Через t часов (t>1) они встретились в точке С и, не останавливаясь, продолжили движение буз изменения направлений .
1. На сколько километров уменьшилось расстояние по шоссе между велосипедистами через 1 час после начала движения?
2. Чему равно расстояние по шоссе между пунктами А и В (в км).
3. На сколько километров больше проехал первый велосипедист нежели второй за время от начала движения до момента встречи?
4. За сколько часов первый велосипедист преодолеет расстояние по шоссе от точки С к пункту В?
Варианты ответов:
А)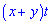 
Б)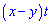 
В)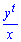 
Г)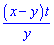 
Д)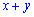 
Решение:
1. За первый час первый велосипедист проехал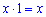 
км, а второй соответственно 
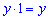км.
Просуммировав получим искомое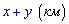 
расстояние, то есть вариант Д.
2. Расстояние от пункта А до места встречи равно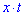 
км и от пункта В к этому же месту 
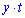км. Добавив эти промежутки мы найдем расстояние от А до В,
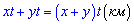
или вариант А.
3. Поскольку скорости велосипедистов постоянные и первого больше на х-у км / ч по сравнению со вторым то за время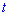 
он проехал 
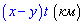больше от старта до момента встречи. Значению соответствует вариант Б.
4. Расстояние от пункта В до точки встречи равно yt км. Первый велосипедист едет со скоростью х км/ч. Чтоб найти время в пути первого велосипедиста нужно расстояние разделить на скорость, то есть за
часов первый велосипедист прибудет в пункт встречи или вариант В.
Ответ: 1-Д); 2-А);3-Б); 4-В).
------------------------------
Задача 22. Установите соответствие между утверждением (1-4) и функцией (А-Д) для которой это утверждение верно.
Утверждение
1. график функции не пересекает одну из осей координат
2. областью значений функции является промежуток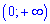 
3. функция убывает на всей области определения
4. на отрезке [-1,5;1,5] функция имеет два нуля
Варианты ответов:
А)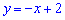 
Б)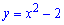 
В)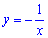 
Г)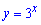 
Д)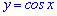 
Решение: Для ответа на указанные вопросы нужно провести анализ на каждое утверждение функций и выяснить для которых они справедливы. Мы же приведем правильные ответы отвергая лишние подробности.
1. График функции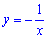 
не пересекает оси координат так как ОДЗ исключает точку х=0 и соответственно не найдется точки при которой ордината будет равна нулю y=0.
2. Областью значений степенной функции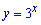 
является промежуток 
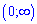- Это должны знать все школьники.
3. Функция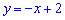 
убывает на всей области определения. В этом легко убедиться найдя первую производную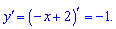 
Она меньше нуля, следовательно функция нисходящая.
4. Функция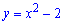 
имеет два корня ( нули) на промежутке [-1,5;1,5].
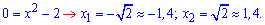
Подытожив все выше сказанное получим конечный результат решения задачи.
Ответ: 1-В); 2-Г) 3-А); 4-Б).
------------------------------
Посмотрите ВНО математика. Решение задач № 11-16 та ВНО математика. Решение задач № 23-28
/
