Решения заданий ВНО-2013 по математике, которые изложены, упростят подготовку к тестированию. Ниже приведены ответы заданий № 11-16 с детальным анализом необходимых действий для получения правильного результата .
------------------------------
Задача 11. Упростите выражение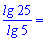 
Варианты ответов :
А)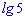 
Б) 5
В)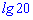 
Г) 2
Д) 0,5
Решение: В таких примерах при тестировании без свойств логарифма не обойтись, но если Вы знаете правила то данная задача решается в одну строку
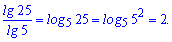
Ответ: Г.
------------------------------
Задача 12. Сторона основания правильной четырехугольной призмы равна 3 см, а периметр ее боковой грани – 22 см. Найдите площадь боковой поверхности этой призмы.
Варианты ответов:
А)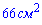 
Б)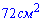 
В)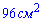 
Г)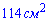 
Д)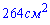 
Решение: Площадь боковой поверхности призмы можно найти через произведение периметра основания на ее высоту
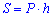
Согласно условию задания четырехугольная призма является правильной, то есть в ее основе лежит квадрат со стороной а=3 см. На этой основе находим периметр
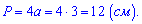
Высоту призмы определим с периметра боковой грани
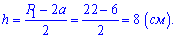
Если этой формулы не знать или не вывести то задача решить не удастся. Площадь боковой поверхности находим по формуле
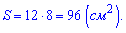
Ответ: В.
-----------------------------
Задача 13. Найдите значение выражения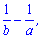 
если
.
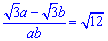Варианты ответов :
А) -2
Б) 0,5
В) 2
Г) 3
Д) 6
Решение: Приведем выражение к общему знаменателю
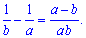
Получили вторую зависимость, только умноженную на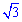 
. Поэтому разделим второй на 
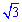и получим ответ
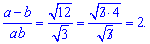
Окончательно имем
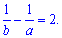
Ответ: В.
------------------------------
Задача 14. В треугольнике АВС задано АС=2 см,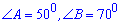 
(см. рисунок ). Определите ВС (в см) по теореме синусов.
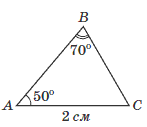
Варианты ответов:
А)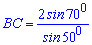 
Б)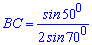 
В)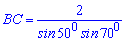 
Г)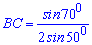 
Д)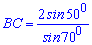 
Решение: Используя теорему синусов выписываем зависимость
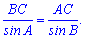
Переписав ее через значения углов
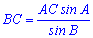
непосредственной подстановкой вычисляем значение стороны
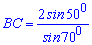
Ответ: Д.
------------------------------
Задача 15. На координатной плоскости ху изображен круг центр которого совпадает с началом координат (см. рисунок). Точки К(8;6) и М(х;у) принадлежат этому кругу . Определите координаты точки М.
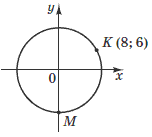
Варианты ответов:
А) (-10;0)
Б) (10;0)
В) (0;-14)
Г) (0;-10)
Д) (0;10)
Решение: Для отыскания координат точки М необходимо установить радиус заданного круга.
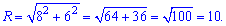
Поскольку точка М находится по оси Оу на круге то ее координаты будут равны
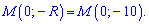
Ответ: Г.
------------------------------
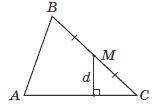
Задача 16. В треугольнике АВС точка М – середина стороны ВС, АС=24 см (см. рисунок). Найдите расстояние d от точки М до стороны АС, если плоскость треугольника АВС равна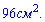 
Варианты ответов:
А) 2 см
Б) 3 см
В) 4 см
Г) 6 см
Д) 8 см
Решение: Площадь треугольника можно определить по классической формуле
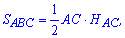
где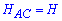 
– высота проведенная к стороне АС.
На основании формулы и данных находим высоту треугольника
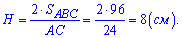
По теореме Фалеса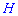 
и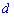 
отсекают пропорциональные отрезки от основания. Получим два подобных треугольника (см. рис. ),
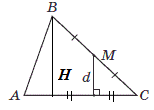
из которых составляем пропорцию для определения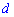 
.
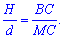
После упрощений получим
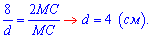
Ответ: B.
------------------------------
Посмотрите ВНО математика. Решение задач № 1-10 та ВНО математика. Решение задач № 17-22
