Знакопеременные и знакочередующиеся ряды. Признак сходимости Лейбница
Кроме знакоположительных рядов на практике встречаются знакопеременные и знакочередующиеся ряды. О них и пойдет реч в данной статье.
Ряд
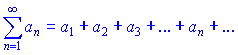
называется знакопеременным, если часть его членов принимает положительные значения, а остальные - отрицательные..
Знакочередующимся называется ряд, соседние члены которого имеют противоположные знаки. В случае когда первый член знакочередующивося ряда положителен, его можно подать в виде
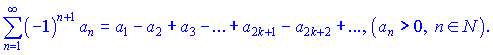
Для исследования сходимости ряда используют признак Лейбница : если члены знакопочережного ряда спадают по абсолютной величине и
![]()
то ряд совпадающий. При этом сумма ряда не превышает значения его первого члена, если он положительной.
Для знакопеременного ряда существуют понятия абсолютной и относительной сходимости.
Знакопеременный (знакопочережний) ряд совпадающий абсолютно если этот ряд и ряд образован из модулей членов этого ряда совпадающие одновременно. Ряд называют условно или неабсолютно совпадающим в случаях, когда совпадающий лишь знакопеременный ряд, а ряд составлен из абсолютных величин членов ряда разбегается
--------------------------------------------
Пример 1.
Исследовать какие ряды совпадают абсолютно, условно или разбегаются
1) (9.131)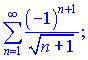
2) (9.132)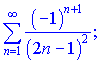
3) (9.133)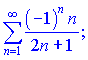
4) (9.134)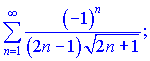
Решение.
1) Данный ряд знакопочережный, а также каждый следующий член по модулю меньше предыдущего
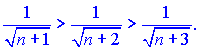
Найдем границу
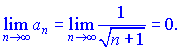
По признаку Лейбница ряд совпадающий. Проверим ряд, составленный из модулей членов на абсолютную сходимость. Применим признак Даламбера
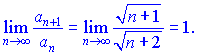
Данный признак ответа не дает. Применим интегральный признак Коши
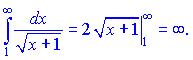
Ряд разбежный поскольку знакопочережний ряд совпадающий, а ряд из модулей разбежный то ряд который решали относительно совпадающий.
2) Каждый следующий член ряда по модулю меньше предыдущего
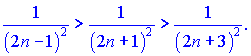
Граница равна нулю
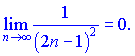
Признак Лейбница выполняется. Проверим на абсолютную сходимость, применим интегральный признак Коши
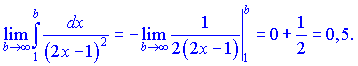
Она подтверждает сходимость ряда, исходный ряд абсолютно совпадающий.
3) Необходимый признак сходимости не выполняется, поскольку каждый следующий член ряда по модулю больше предыдущего
![]()
Ряд разбежный.
4) Члены ряда убываают
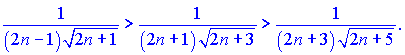
Найдем границу
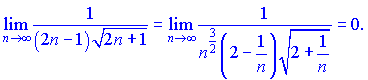
Следовательно ряд совпадающий по признаку Лейбница, проверим на абсолютную сходимость. Из вида делаем выводы что признак Делабера ничего не даст. Применим интегральный признак Коши
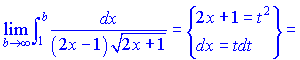
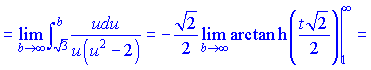
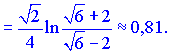
Данный ряд совпадающий, следовательно ряд абсолютно совпадающий.
----------------------------------------------
------------------------------


