Пусть задана бесконечная последовательность чисел ![]() Бесконечная сумма чисел вида
Бесконечная сумма чисел вида ![]() -- называется числовым рядом, а числа
-- называется числовым рядом, а числа ![]() -членами ряда.
-членами ряда.
Ряд обозначают так:
![]()
Выражение для ![]() - го члена ряда при произвольном натуральном
- го члена ряда при произвольном натуральном ![]() >0 , называется общим членом ряда и обозначается
>0 , называется общим членом ряда и обозначается ![]() .
.
Общий член ряда можно задать формулой![]() , помощью которой записывается произвольный член ряда.
, помощью которой записывается произвольный член ряда.
Сумму первых его ![]() членов обозначают через
членов обозначают через ![]() :
:
![]()
и принято называть ![]() -ой частичной суммой ряда.
-ой частичной суммой ряда.
Частичные суммы ряда образуют некоторую числовую последовательность его частичных сумм ![]() . Ряд называется совпадающим, если совпадает последовательность его частичных сумм
. Ряд называется совпадающим, если совпадает последовательность его частичных сумм ![]() , то есть если существует збежная граница
, то есть если существует збежная граница
![]()
Число ![]() при этом называют суммой ряда и записывают
при этом называют суммой ряда и записывают
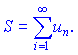
При этом считают также что ряд стремитса к числу![]() .
.
Если последовательность частичных сумм ряда разбегается то ряд называется разбежным. В этом случае ряд не имеет суммы.
Ряд составленный из элементов геометрической прогрессии называется геометрическим рядом:
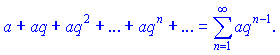
Число ![]() — знаменатель геометрической прогрессии.
— знаменатель геометрической прогрессии.
Обозначим через ![]() сумму
сумму ![]() первых членов прогрессии и найдем ее значение:
первых членов прогрессии и найдем ее значение:
![]()
![]()
Отсюда получаем
![]()
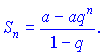
Если![]() , то
, то
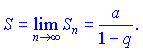
геометрический ряд збегается.
Если![]() , то
, то
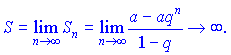
Если![]() , то
, то
![]()
Если ![]() , то
, то
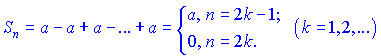
таким образом, последовательность ![]() - разбежная.
- разбежная.
Ряд вида
![]()
называется гармоническим рядом и являеться разбежним.
Числовой ряд вида
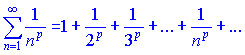
называется обобщенным гармоническим рядом. Доказано, что при ![]() обобщенный гармонический ряд разбегается, а при
обобщенный гармонический ряд разбегается, а при ![]() -ряд сходится.
-ряд сходится.
Если ряд совпадает, то разница между суммой ![]() и частичной его суммой
и частичной его суммой ![]()
![]()
называется ![]() -м остатком ряда.
-м остатком ряда.
Остаток ряда ![]() являет собой ту погрешность которая получится, если вместо приближенного значения суммы ряда
являет собой ту погрешность которая получится, если вместо приближенного значения суммы ряда ![]() взять сумму первых
взять сумму первых ![]() членов этого ряда. Но поскольку
членов этого ряда. Но поскольку ![]() ето граница суммы, то для совпадающего ряда выполняется
ето граница суммы, то для совпадающего ряда выполняется
![]()
Таким образом взяв достаточно большое число членов совпадающего ряда можно сумму этого ряда вычислить с большой точностью. Отсюда выплывает что основной задачей теории рядов является исследование сходимости ряда.
{jcomments off}


