Функциональным рядом называется ряд составлен из членов, которые являются функциями от аргумента 
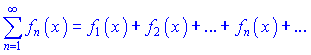
При каждом конкретном значении аргумента 
с области определения 
функциональный ряд превращается в числовой.
Если для 
числовой ряд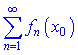 
сходится, то говорят что функциональный ряд сходится в точке 
, а саму точку называют точкой сходимости.
Множество всех значений переменной 
при которых функциональный ряд сходиться называется областью сходимости ряда. На практике рассматривают ряды, областями сходимости которых являются разные интервалы оси 
.
В точках с области сходимости ряда существуют значение суммы ряда 
, а также можно установить зависимость между точками сходимости и значениями сумм. Таким образом, сумма функционального ряда является функцией 
, область определения которой идентична области сходимости функционального ряда. При этом, говорят что функциональный ряд сходится к функции 
, или функция разлагается в ряд
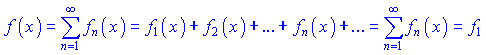
в его области сходимости. Функциональный ряд вида
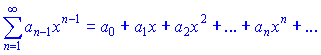
где 
постоянные коэффициенты называют степенным рядом.
Часто рассматривают степенной ряд более общего вида
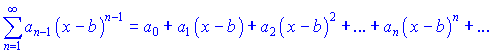
где 
ПРИЗНАК ВЕЙЕРШТРАСА
Функциональный ряд вида
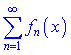
абсолютно и равномерно сходящийся на промежутке
, если существует знакоположительный сходящийся числовой ряд
такой, что для всех
выполняется условие
ПРИЗНАК СХОДИМОСТИ СТЕПЕННОГО РЯДА
Теорема Абеля. Если степенной ряд сходится в точке
, то он сходится абсолютно в интервале
Если степенной ряд расходится в точке 
, то он будет расходящийся для всех 
, удовлетворяющих условие
Число 
называют радиусом сходимости степенного ряда, а промежуток 
- интервалом сходимости (областью сходимости). Если все коэффициенты ряда ненулевые, то радиус сходимости равен следующей границе
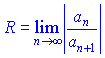
при условии, что она существует (конечное или бесконечное).
Для рядов вида
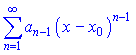
радиус сходимости определяется по формуле 
, однако интервал сходимости из неравенства
Теорема не дает ответа о сходимости на концах интервала, поэтому их следует проверять отдельно по известным признакам сходимости.
Рассмотрим примеры на нахождение области сходимости степенного ряда.
--------------------------------------------
Пример 1. Найти область сходимости функционального ряда
(9.181)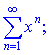 
Решение. Данный ряд знакоположительный. Для того, чтобы исполнялись необходимое условие сходимости нужно, чтобы ряд был монотонно нисходящим
Поделив на 
получим, что это выполняется при условии
Итак, областью сходимости данного ряда будет интервал
Пример 2. Найти область сходимости функционального ряда
(9.182)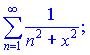 
Решение. По признаку Вейерштрасса данный ряд сходится для всех 
, поскольку каждый член ряда
меньше соответствующего члена ряда
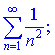
который является сходящимся. Таким образом, получаем следующую область сходимости -
Пример 3. Определить область сходимости функционального ряда
(9.183)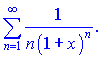 
Решение. Данный ряд от гармоничного отличается множителем в знаменателе
Если этот множитель по модулю будет больше единицы, то ряд будет сходиться. Из этого условия получим
Для данного ряда получили два промежутка 
на которых ряд будет сходиться.
--------------------------------------------
Пример 4. Найти область сходимости степенного ряда
(9.211)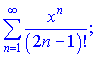 
Решение. Найдем радиус сходимости ряда
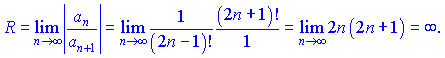
Радиусом сходимости будет интервал 
Пример 5. Определить область сходимости степенного ряда
(9.212)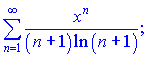 
Решение. Вычислим предел
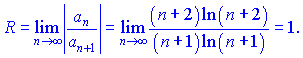
Интервал сходимости равен 
Исследуем поведение следующих рядов
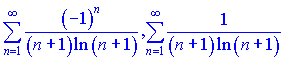
чтобы дать ответ о сходимости на краях.
Первый ряд - знакочередующийся. По признаку Лейбница
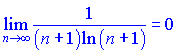
ряд сходится.
Второй ряд проверим согласно интегральному признаку Коши
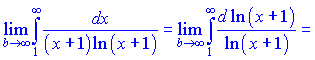
Данный ряд расходится. Таким образом интервалом сходимости ряда будет промежуток 
Пример 5. Определить область сходимости степенного ряда
(9.213)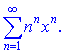
Решение. Найдем 
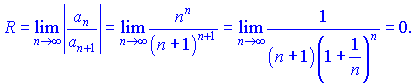
Радиус сходимости ряда равен нулю, а это значит что ряд сходится в точке
.
Вот примерно такие задания ждут Вас на контрольной работе или экзаменах. Выучите методику проверки ряда на сходимость и получите в зачетку хорошую оценку.
