"Найти разложение в ряд Маклорена функци f(x)" - именно так звучит задание по высшей математике, которое одним студентам по силам, а другие не могут справиться с примерами. Есть несколько способов разложения ряда по степенях, здесь будет дана методика разложения функций в ряд Маклорена. При развитии функции в ряд нужно хорошо уметь вычислять производные.
Пример 4.7 Разложить функцию в ряд по степеням x
![]()
Вычисления: Выполняем разложение функции согласно формуле Маклорена. Сначала разложим в ряд знаменатель функции
![]()
напоследок умножим разложение на числитель.
Первое слагаемое - значение функции в нуле f (0) = 1/3.
Найдем производные функции первого и высших порядков f (x) и значение этих производных в точке x=0
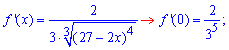
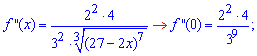
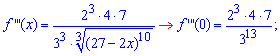
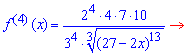
![]()
Далее с закономерности изменения значения производных в 0 записываем формулу для n-й производной
![]()
Итак, знаменатель представим в виде разложения в ряд Маклорена
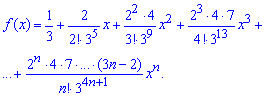
Умножаем на числитель и получаем искомое разложение функции в ряд по степеням х
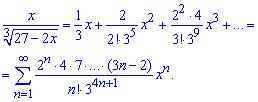
Как видите ничего сложного здесь нет.
Все ключевые моменты базируются на умении вычислять производные и быстрому обобщении значение производной старших порядков в нуле. Следующие примеры помогут Вам научиться быстро раскладывать функцию в ряд.
Пример 4.10 Найти разложение в ряд Маклорена функции
![]()
Вычисления: Как Вы возможно догадались раскладывать в ряд будем косинус в числителе. Для этого можете использовать формулы для бесконечно малых величин, или же вывести разложение косинуса через производные. В результате придем к следующему ряду по степеням x
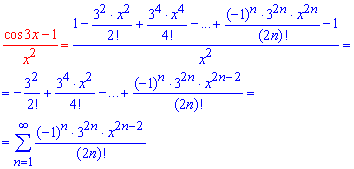
Как видите имеем минимум вычислений и компактную запись разложения в ряд.
Пример 4.16 Разложить функцию в ряд по степеням x:
7/(12-x-x^2)
Вычисления: В подобного рода примерах необходимо дробь разложить через сумму простейших дробей.
Как это делать мы сейчас не будем показывать, но с помощью неопределенных коэффициентов придем к сумме дох дробей.
Далее записываем знаменатели в показательной форме
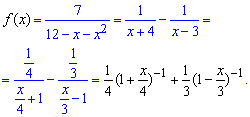
Осталось разложить слагаемые с помощью формулы Маклорена. Подытоживая слагаемые при одинаковых степенях "икс" составляем формулу общего члена разложения функции в ряд
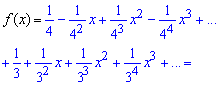
![]()
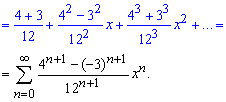
Последнюю часть перехода к ряду в начале трудно реализовать, поскольку сложно объединить формулы для парных и непарных индексов (степеней), но с практикой у Вас это будет получаться все лучше.
Пример 4.18 Найти разложение в ряд Маклорена функции
![]()
Вычисления: Найдем производную этой функции:
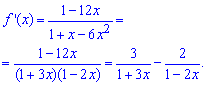
Разложим функцию ![]() в ряд, воспользовавшись одной из формул Макларена:
в ряд, воспользовавшись одной из формул Макларена:
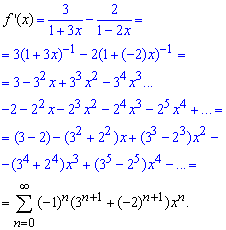
Ряды почленно суммируем на основе того, что оба абсолютно совпадающие. Проинтегрировав почленно весь ряд получим разложение функции в ряд по степеням x
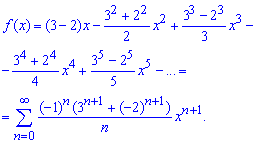
Между последними двумя строками разложения имеется переход который в начале у Вас будет забирать много времени. Обобщение формулы ряда не всем дается легко, поэтому не переживайте по поводу того что не можете достать красивой и компактной формулы.
Пример 4.28 Найти разложение в ряд Маклорена функции:
![]()
Запишем логарифм следующим образом
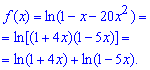
По формуле Маклорена раскладываем в ряд по степеням x логарифм функцию
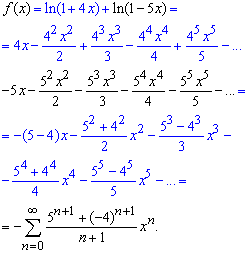
Конечное свертывания на первый взгляд сложное, однако при чередовании знаков Вы всегда получите нечто подобное. Входной урок по теме расписания функций в ряд завершено. Другие не менее интересные схемы разложения будут подробно рассмотрены в следующих материалах.


