Степенные и функциональные ряды могут быть сходящимися на множестве действительных чисел, на определенном интервале, или быть расходящимися. Установка радиуса сходимости и области сходимости ряда является важным при исследовании рядов. Радиус сходимости равный половине ширины области сходимости. На практике обе характеристики найти не трудно и Вы в этом скоро убедитесь.
Пример: 3.6 Найти радиус сходимости и область сходимости степенных рядов:
а)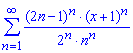 
Вычисления: Для оценки сходимости ряда составим ряд с модулей членов заданного ряда, то есть ряд с последующим общим членом
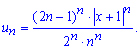
Далее, исходя с того что полученный ряд имеет положительные члены - исследовать его на сходимость будем с помощью признака Даламбера:
Для этого выписываем следующий после общего член ряда
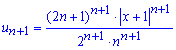
и подставляем в формулу предела. Вид членов ряда непрост, поэтому будьте внимательны при упрощении предела
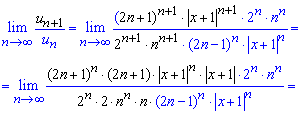
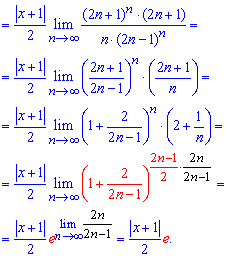
Наконец приходим к экспоненте и функциональному множителю.
Если граница меньше единицы
то ряд сходится по теореме Даламбера, причем абсолютно.
Отсюда составляем ограничения на допустимые "иксы"
- область сходимости ряда.
Итак, ми нашли 
- радиус сходимости и
- область сходимости ряда в виде интервала.
Для себя запомните, что радиус сходимости функционального ряда равен половине расстояния между крайними точками области сходимости.
б) 
Вычисления: Составим ряд из модулей членов заданного ряда, то есть с общим членом
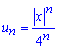
Нетрудно видеть что такой прием позволяет получить ряд с положительными членами и при этом исследовать его на сходимость с помощью признака Даламбера.
Для предела нам еще нужен следующий член ряда
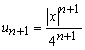
Подставляем члены ряда в предел и вычисляем
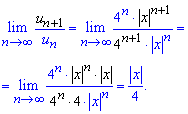
При пределе меньшей единицы 
- ряд убывает за Даламбером.
Из этого условия находим
- область сходимости в виде ограничений переменной.
В итоге мы нашли R=4 - радиус сходимости ряда и его область сходимости 
Пример: 3.11 Найти радиус сходимости и область сходимости степенного ряда:
а)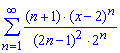 
Вычисления: Члены заданного функционального ряда
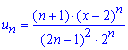
определены на всей действительной оси, то есть область определения следующая
Составляем ряд из модулей членов заданного ряда
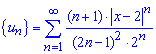
Его общий член может бить выражен формулой
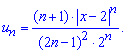
Поскольку новый ряд имеет положительные члены - исследуем на сходимость по Даламберу:
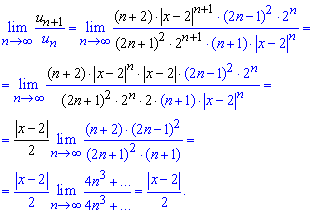
При 
- ряд совпадает по теореме Даламбера, то есть необходимо, чтобы выполнялись условия
Отсюда находим R = 2 - радиус сходимости ряда и (0; 4) - область сходимости.
б)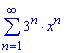 
Вычисления: Члены заданного функционального ряда
определены для всех действительных переменных 
то есть область определения следующая
Составим ряд из модулей членов заданного ряда
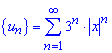
Снова применяем признак Даламбера для исследования ряда на сходимость
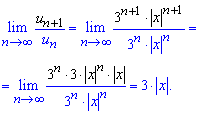
За Даламбером при пределе меньше единицы
- ряд убывает.
Отсюда находим область сходимости
и R=1/3 радиус сходимости. Из приведенных примеров
Вы могли увидеть такую закономерность что значение которое ограничивает модуль с переменной и является радиусом сходимости ряда.
Область сходимости имеет в два раза большую длину и определяется раскрытием модуля.
Пример: 3.17 Найти радиус сходимости и область сходимости степенных рядов:
а)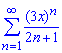 
Вычисления: Члены функционального ряда
определены при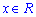 
то есть 
Составим ряд из модулей членов заданного ряда
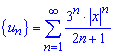
то есть
Исследуем его на сходимость по признаку Даламбера. Выписываем следующий после общего члена ряда
и подставляем в предел
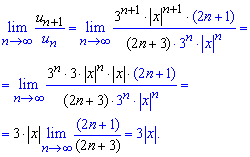
При 3|x|<1 - ряд убывает,
отсюда находим
– область сходимости ряда.
Все что находится справа от модуля это R = 1/3 - радиус сходимости ряда, а ограничения на "икс"
– это область сходимости.
б)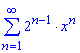 
Вычисления: Члены функционального ряда
определены на всей действительной прямой 
, их область определения имеет вид 
.
По схеме составляем ряд из модулей членов заданного ряда
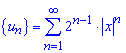
и получаем ряд со следующим общим членом
Образованный ряд будем анализировать на сходимость по признаку Даламбера
Выписываем следующий член ряда
и подставляем в предел
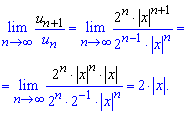
При 2|x|<1- ряд будет сходящимся.
Раскрываем модуль и находим
- область сходимости и R=1/2 – радиус сходимости.
В виде интервала записываем область сходимости ряда
Пример: 3.27 Найти радиус сходимости и область сходимости степенного ряда
а)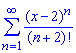 
Вычисления: Члены функционального ряда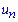 
определены на действительной оси 
Сначала составим ряд из модулей членов этого ряда
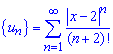
Общий член задается формулой
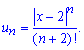
Исследуем ряд с модулей на сходимость по признаку Даламбера:
Находим предел отношения следующего члена ряда общему
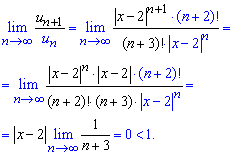
Поскольку A=0<1 то ряд сходится при всех действительных переменных, то есть имеет неограниченную 
- область сходимости.
Ряд имеет бесконечный 
радиус сходимости.
б)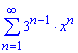 
Вычисления: Члены ряда 
определены на множестве действительных чисел
Построим ряд с модулей членов ряда:
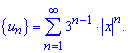
Далее записываем общий и следующий после него члены ряда
и подставляем в предел
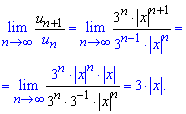
По теореме Даламбера ряд сходится при
3|x|<1. Из этого условия определяем
-
область сходимости ряда
и R=1/3 – радиус сходимости.
В виде интервала записываем в ответ область сходимости 
Теперь Вы знаете как найти область сходимости и радиус сходимости ряда. Пользуйтесь приведенными формулами и успешной Вам сдачи сессии.
