Разложение функции в ряд интегрированием производной

Одним из методов разложения функции в ряд является вычисление производной функции, дальше производную развивают в ряд (формулы Маклорена) и интегрированием находят разложение функции. На словах это выглядит несколько запутанно, однако следующие примеры должны раскрыть суть этой методики.

Пример 5.8 Разложить арктангенс в ряд по степеням x:

Вычисления: Напрямую раскладывать арктангенс я бы никому не советовал, поэтому сначала вычислим производную функции:

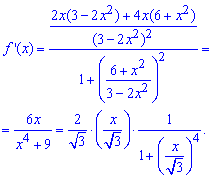
Обозначим за новую переменную , тогда производную можем записать в виде

Далее знаменатель производной по формулам Макларена раскладываем в ряд

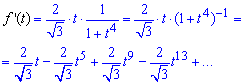
Возвращаясь к замене, получим разложение производной

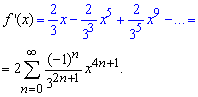
После этого почленно интегрируем весь ряд и получим конечную формулу разложения арктангенса

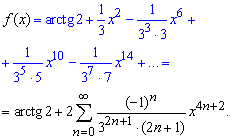
Вычислений много, но на практике задачи бывают не легче.

Пример 5.13 Найти разложение арктангенса в ряд по степеням x

Вычисляем производную от арктангенса, как от сложной функции

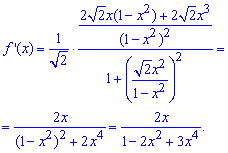
Упрощение позволяют получить компактный выражение производной Далее записываем расписание производной 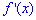в ряд с неопределенными коэффициентами



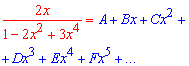
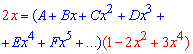
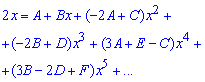
Полной схемы приводить сейчас не будем, однако если перенести знаменатель по правую сторону от знака равенства и приравнять коэффициенты при одинаковых степенях переменной x то получим разреженную систему уравнений и в конце ее решение:
A=0, B=2, C=0,D=4,E=0, F=2, ….
После этого можем записать разложение производной в виде

Если запись проинтегрировать, то получим расписание функции по степеням x

Формула несмотря на сложность расчетов, достаточно компактна.

Пример: 5.19 Найти разложение арксинуса в ряд по степеням x

Вычисления: По приведенной выше схеме сначала находим производную как от сложной функции:

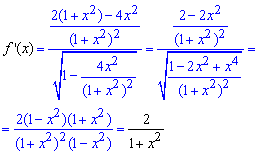
Раскладываем производную 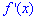в ряд по формуле Маклорена

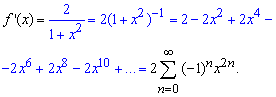
Интегрирования ряда не вызывает никаких проблем и мы получаем финальный расклад арксинуса в ряд


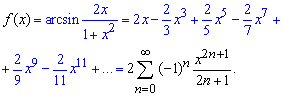
Пример: 5.29 Разложить логарифм в ряд по степеням x

Вычисления: Под логарифмом имеем сложную функцию, поэтому по правилу сначала дифференцируем логарифм, а затем умножаем на производную от функции в скобках

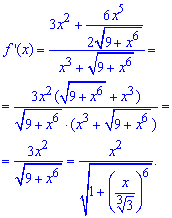
По формулам Маклорена раскладываем производную логарифма, а вернее ее знаменатель в ряд по степеням x

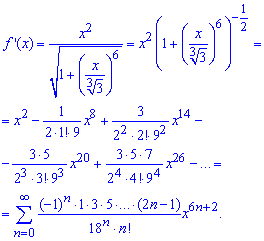
Общий член ряда содержит как показательную так и факториальную зависимость от индекса. Интегрируем члены ряда и, учитывая что f(0)=ln(3), получим разложение логарифма по степеням переменной x

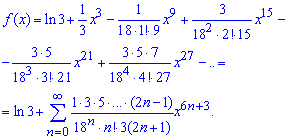
На этом знакомство с разложение функции в ряд Маклорена подходит к концу, больше примеров Вы найдете в следующих статьях.