Ряд вида
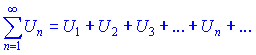
называется положительным, если все его члены неотрицательные
Для определения сходимости в литературе собраны правила которые позволяют это быстро определить. Рассмотрим по очереди признаки сходимости числовых рядов
Признак сравнения
Рассмотрим два ряда с положительными членами
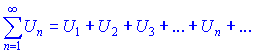
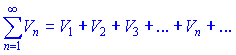
Для них выполняются следующие утверждения:
1. Если члены ряда 
не больше соответствующих членов 
сходящегося ряда 
(
) то ряд 
сходится.
Если каждый член ряда 
больше (или ровный) соответствующего члена росходящегося ряда 
то ряд 
разбегается.
--------------------------------------------
Пример 1.
Исследовать на сходимость ряды
1) 
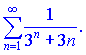
2) 
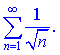
Решение.
1) Сравним заданный ряд
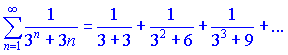
с рядом геометрической прогрессии знаменатель которой равен 
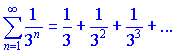
Каждый член первого ряда меньше соответствующего член ряда геометрической прогрессии, который сбегается, поскольку
По признаку сравнения первый ряд сходится.
2) Члена данного ряда сравниваем с соответствующими гармонического ряда. Для произвольного 
выполняется неравенство
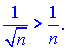
Так как гармонический ряд разбежный то в соответствии с признаком сравнения заданный ряд также разбежный.
--------------------------------------------
Предельный признак сравнения
Пусть ряды 
и 
положительные, а также существует предельная граница
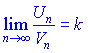
причем 
, тогда оба ряда или одновременно совпадающие или одновременно разбежные.
--------------------------------------------
Пример 2.
Исследовать на сходимость ряд
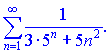
Решение.
Для сравнения выберем ряд 
совпадающей геометрической прогрессии. Применяя предельный признак будем иметь
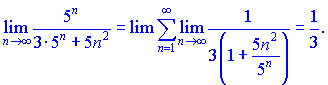
Поскольку оба ряды ведут себя равносильно 
, а геометрический ряд сходится, то и рассмотренный ряд также сходится.
--------------------------------------------
Признак Даламбера
Пусть члены ряда
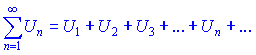
положительные и отношение 
-го члена до 
-го имеет предел при
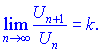
Если
то ряд сходится,
если 
- ряд расходится.
При 
надо применять другой признак сходимости, поскольку данный признак не может определить сходится ряд или расходится.
--------------------------------------------
Пример 3.
Исследовать на сходимость ряды
1) 
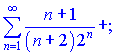
2) 
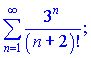
3) 
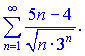
Решение.
1) Найдем границу отношения 
члена до 
-го при 
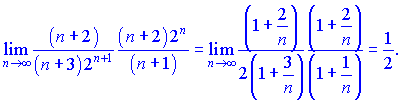
Поскольку 
то ряд сходится.
2) Вычислим границу
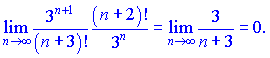
Ряд сходящийся, так как 
3) Применим признак Даламбера
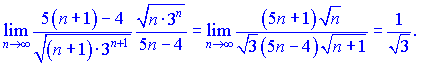
Видим что ряд сходящийся поскольку
------------------------------------------
Радикальный признак Коши
Если для ряда 
положительными членами существует граница
то при 
ряд сходится, а при 
- разбегається.
При 
нужно применять другой признак сходимости.
-------------------------------------------
Пример 4.
Исследовать на сходимость ряды
1) 
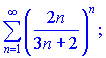
2) 
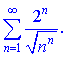
Решение.
1) Применим признак Коши
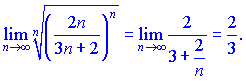
Ряд совпадающий поскольку
2) Вычислим границу
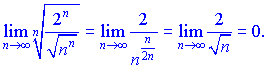
Данный ряд также совпадающий, поскольку 
--------------------------------------------
Интегральный признак Коши
Пусть задан ряд
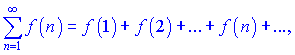
причем функция
положительная, непрерывная и монотонно нисходящая функция от переменной 
. Тогда
1) ряд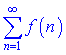 
совпадающий, если несвойственный интеграл
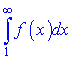
совпадающий;
2) ряд разбежный когда интеграл разбежный.
Под сходимостью интегралу следует понимать его ограниченность, то есть
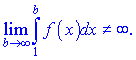
Рассмотрим примеры применения интегрального признака Коши.
--------------------------------------------
Пример 5.
Исследовать на сходимость
1) 
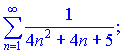
2) 
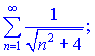
3) 
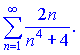
Решение.
1) Применим интегральный признак Коши
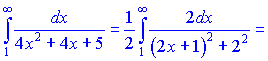
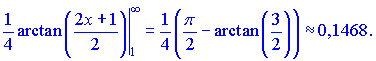
Ряд совпадающий поскольку интеграл совпадающий.
2) Найдем интеграл
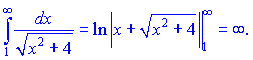
По интегральному признаку Коши ряд разбежный.
3) Вычислим интеграл
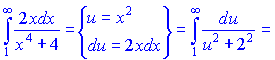
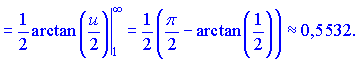
Данный ряд совпадающий.
----------------------------------------------
------------------------------
