Неоднородные дифференциальные уравнения вычисляют немного больше времени чем однородные, кроме однородного решения необходимо установить частичное решение неоднородного ДУ. На практике это отражается в решении двух разных по схеме вычислений ДУ. Если еще есть условие Коши напоследок всех поисков решения дифференциального уравнения необходимо определить значение постоянных, входящие в функцию. Все это достаточно просто реализуется, поэтому переходим к анализу готовых ответов.
Пример 1. Найти решение задачи Коши для дифференциального уравнения
Решение: Имеем неоднородное дифференциальное уравнение первого порядка. Как поступать с такими уравнениями подробно рассмотрены на предыдущих уроках.
Найдем сначала решение однородного ДУ. Интегрируем для этого уравнения (левую часть), предварительно разделив переменные:
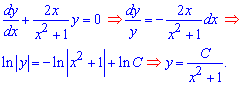
Далее считаем, что стала С(х) является функцией от переменной x
Все это делается для того, чтобы подобрать постоянную таким образом, чтобы удовлетворить неоднородную функцию - правая часть ДУ.
Найдем производную y' с учетом выше сказанного
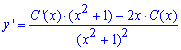
Подставляем функцию и ее производную в исходное дифференциальное уравнение
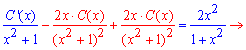
Видим, что двое слагаемых при суммировании дадут ноль и в результате получим зависимость для производной от постоянной
Из последнего уравнения методом интегрирования находим явный вид постоянной С(x)
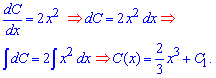
После этого можем записать общее решение уравнения
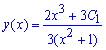
Но это еще не финал вычислений, нам нужно найти частичный решение (задача Коши). Для этого удовлетворяем начальное условие на функцию и вычисляем постоянную
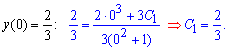
Итак, задача Коши решена и найдено частичное решение дифференциального уравнения в виде
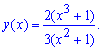
На этом одно из уравнений вычислено. Схема нахождения функции не слишком запутана с одной стороны, с другой ее легко реализовать (постоянную принимаем за функцию). Рассмотрим еще несколько готовых примеров, а дальше учитесь вычислять самостоятельно.
Пример 2. Решить задачу Коши для уравнения
Решение:Имеем неоднородное дифференциальное уравнение первого порядка + условие Коши. Запишем и проинтегрируем соответствующее однородное уравнение, предварительно разделив переменные
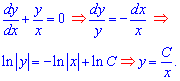
Решение однородного уравнения найти в данном случае довольно легко. Изучите для практики внесения сталой в интегралах под логарифм - это значительно упростит дальнейшие преобразования с решением. Далее рассмотрим константу C как функцию от переменной x
Производная y' по формуле примет выражение
Подставим функцию y и ее производную y' в исходное дифференциальное уравнение и выразим производную постоянной
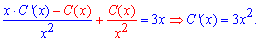
Интегрированием находим недостающую зависимость C(x)
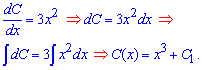
Заменив постоянную полученным только что значением, получим общее решение дифференциального уравнения
Решим задачу Коши. С начального условия имеем
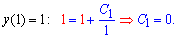
Определив сталую получим y=x2 - частичное решение дифференциального уравнения.
Пример 3. Найти решение дифференциального уравнения и задачи Коши
Решение:Начнем с анализа левой части дифференциального уравнения. Интегрируем однородное дифференциальное уравнение, предварительно отделив в нем переменные
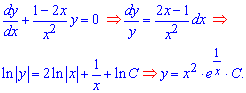
Для последнего перехода использовали свойство экспоненты - второе слагаемое записали как логарифм от экспоненты ln(exp(1/x)).
Теперь предположим, что константа C(x) - это функция от переменной x:
тогда ее производная равна
Подставляем постоянную и ее производную в исходное дифференциальное уравнение
которое после сокращения слагаемых превратится в зависимость
Из последнего уравнения функцию C(x) находим интегрированием
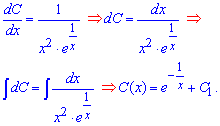
Итак, мы нашли общее решение дифференциального уравнения
Найдем частичное решение уравнения (задача Коши). Удовлетворим начальное условие на функцию и вычислим постоянную
Отсюда имеем y=x2 - частичное решение уравнения. На вид простая запись, хотя на ее вычисления потрачено немало времени.
Частичное решения двух последних примеров совпадают, такое редко бывает на практике. Теперь Вы знаете, как решить неоднородное уравнение и выполнить условие Коши.
Если на экзамене или контрольной работе Вам нужна помощь - обращайтесь. Мы помогли не одной тысячи студентов, сможем помочь и Вам.
