Все кто ищет готовые ответы на линейные дифференциальные уравнения пришли по правильному адресу. У нас Вы сможете не только получить быстрый ответ, но и научиться методике решения уравнений. Будет ли сложной схема Бернулли для линейных уравнений зависит от Вашего уровня подготовки. Разберите внимательно приведенные ответы и сделайте выводы, что и как Вам нужно углубленно изучить.
Линейным дифференциальным уравнением первого порядканазывается уравнение вида y'+p(x)*y=g(x), где p(x) и g(x) – непрерывные на определенном промежутке функции.
Алгоритм метода Бернулли
1. Решение линейного дифференциального уравнения необходимо представить в виде произведения двух неизвестных функций y=u*v от аргумента u=u(x),v=v(x). Одну из этих функций можно выбрать произвольно, а вторая определяется из дифференциального уравнения.
2. По правилу производная произведения равна y=u*v,то y'=u'v+uv'.
3. Подставим запись функции y=u*v и производной y'=u'v+uv' в уравнение y'+p(x)*y=g(x) и получим u'v+uv'+p(x)*u*v= g(x). Сгруппируем второй и третий слагаемые, вынеся общий множитель (u) за скобки и придем к диф. уравнению u'v+u(v'+p(x)*v)=g(x).
4. Сперва определяем частное решение v=v(x), для этого решаем диф. уравнения v'+p(x)*v=0 и за произвольную постоянную интегрирования берем ноль (С=0). Данное уравнение является дифференциальным уравнением с разделяющимися переменными.
5. Далее подставим найденную функцию v=v(x) в исходное диф. уравнение u'v+uv'+p(x)*u*v= g(x), которое при этом упростится до вида u'v+u*0=g(x), то есть к дифференциальному уравнению с разделяющимися переменными u'v(х)=g(x) относительно u(x). Из этого уравнения находим u=u(x)+С.
6. Имея u=u(x) и v=v(x) находим общее решение ДУ через произведение y=u*v=( u(x)+С)* v(x).
7. Если задана задача Коши то с дополнительной условия на решение y(x0)=y0 определяем сталую С.
Пример 1. Найти решение задачи Коши
Решение:Имеем неоднородное дифференциальное уравнение первого порядка. Запишем его в правильном виде, для этого перенесем в правую сторону функцию
Далее по схеме Бернулли делаем замену переменных y=u*v, y'=u'v+uv', где u=u(x) і v=v(x).
Учитывая что множители в левой части уровне
и y2=u2v2
получим следующее уравнение
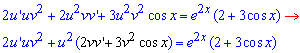
Согласно алгоритму Бернулли уравнение разделим на 2, для этого дужку слева (выделена черным) приравняем к нулю
Сводим к дифференциальному уравнению с разделенными переменными
и решаем интегрированием
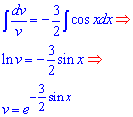
В результате получили экспоненту с отрицательным показателем синуса. При этом исходное дифференциальное уравнение достаточно упростится для поиска второй неизвестной пока функции
Перенесем экспоненту с отрицательным показателем в правую сторону
и сведем к ДУ с разделенными переменными
Интегрированием уравнения в дифференциалах
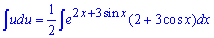
находим решение дифференциального уравнения
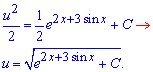
Как описано в начале, общее решение дифференциального уравнения равно произведению функций
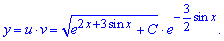
Но это еще не конечная ответ к задаче. Найдем частичное решение дифференциального уравнения (задача Коши), для этого определим постоянную с начального условия на функцию
Сталая равна нулю, это позволяет упростить формулу решения диф. уравнения, хотя мало кто из Вас увидит эту подсказку
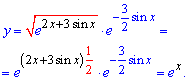
Мы нашли частичный решение дифференциального уравнения и он равен экспоненте в степени "икс" y=ex.
Пример 2. Решить дифференциальное уравнение та задачу Коши
Решение:Задано неоднородное дифференциальное уравнение первого порядка, которое перепишем в виде
Выполняем замену переменных в уравнении
, где "у" и "в" принимают функциональные зависимости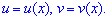 
Находим выражения которые фигурируют в записи
и подставляем в исходное дифференциальное уравнение
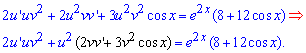
Далее схема вычислений заключается в разделении переменных. По алгоритму Бернулли выражение, содержащее "v" приравняем к нулю
Записываем уравнение в дифференциалах
Видим что имеем уравнение с разделяющимися переменным, поетому целесообразно разделить переменные
Проинтегрировав обе части
получим логарифм и синус.
Далее экспонируем обе части и таким образом находим одну из неизвестных функций
Исходное дифференциальное уравнение при этом упростится к виду
Экспоненту в отрицательном показателе переносим вправо от знака равенства
Далее распишем уравнения через дифференциалы (/2)
и сведем к уравнению с разделенными переменными
Интеграл в правой части выглядит тяжелым для высчисления, но если внести дужку под дифференциал, то получим показатель экспоненты
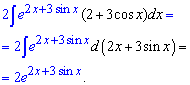
Окончательно после интегрирования получим
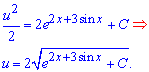
Общий интеграл дифференциального уравнения записываем через произведение функций
Чтобы найти частичное решение дифференциального уравнения (задачи Коши) используем начальное условие
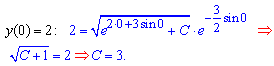
Из него определим постоянную и подставим в уравнение частного решения дифференциального уравнения
На этом и построен алгоритм Бернулли вычислений дифференциальных уравнений такого типа. Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.
