Для практического ознакомления с таблицей основных формул дифференцирования рассмотрим примеры.
Пример 1.
Вычислить производные
1) 
2) 
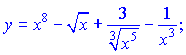
3) 
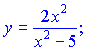
4) 
5) 
6) 
7)
Решение.
1) По формулам дифференцирования (1), (3), (9) получим
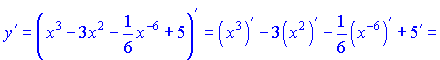
2) Вводим дробные и отрицательные степени и превращаем заданную функцию к виду
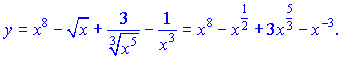
Используя формулы (3), (4), (9) находим
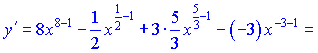
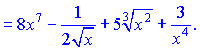
3) Данный пример вычисляем по правилу (6)
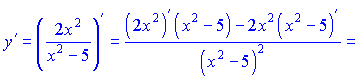
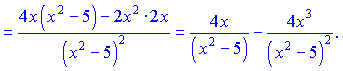
4) Производную функции 
ищем по правилу сложной функции (7)
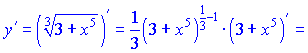
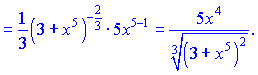
5) Производные от функции
находим по правилу производной от произведения функций, и правилом производной от сложной функции
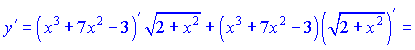
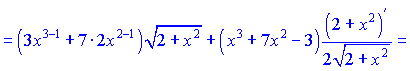
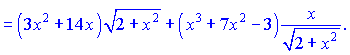
6) По правилу производной от сложной функции будем иметь
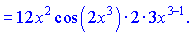
7) Много студентов которые еще толком не знают правил, сначала подносят к квадрату выражение в скобках
а затем проводят дифференцировки. Это неправильно, долго и трудно. Воспользовавшись правилом дифференцирования сложной функции получим
Если Вы будете подносить к квадрату, а затем дифференцировать то получите многочлен, который еще предстоит свести к компактному виду. Результат будет правильный, но зачем идти сложным путем, если за нас уже давно придумали правила дифференцирования, которые упрощают вычисления.
Изучайте их и пользуйтесь на практике.
