Метод логарифмического дифференцирования становится пригодным при дифференцировании произведения нескольких функций или их частки. Его удобно применять при дифференцировании выражений, содержащих корни из дробей (функций), а также когда показатель функции также представляет собой функцию ![]()
В таких случаях целесообразно обе части выражения сначала прологарифмировать по основанию ![]() , а затем приступить к дифференцировке. Этот способ получил название логарифмического дифференцирования. Производную логарифма функции называют логарифмической производной. Суть метода с помощью формул можно описать следующим образом:
, а затем приступить к дифференцировке. Этот способ получил название логарифмического дифференцирования. Производную логарифма функции называют логарифмической производной. Суть метода с помощью формул можно описать следующим образом:
имеем сложную функцию вида
![]()
к обеим сторонам применяем логарифмирования
![]()
находим производные правой и левой части равенства
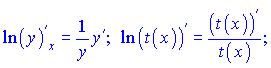
Приравниваем производные и выражаем ![]()
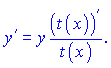
В этом суть метода, дальше все зависит от функции ![]() .
.
Если она представляет собой произведение функций
![]()
то по свойствам логарифма он будет равен сумме логарифмов
![]()
Если имеем дробь от функций
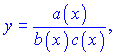
то применяя логарифмирования получим
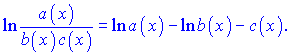
Если имеем функцию в степени другой
![]()
то по свойствам логарифма получим
![]()
В случае корней ![]() дифференцировки значительно упрощается
дифференцировки значительно упрощается
![]()
Дальнейшее вычисление производных зависит от сложности самих функций. Рассмотрим конкретные примеры, чтобы данный материал стал для Вас более понятным и наглядным.
Задача.
Используя логарифмирования найти производную (Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")
1) (5.2.178)![]()
2) (5.2.191)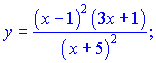
3) (5.2.195)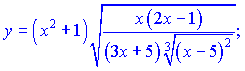
4) (5.2.199)![]()
Решение.
Примеры выбрано сложные для того, чтобы раскрыть всю силу метода логарифмического дифференцирования и рассмотреть типичные распространенные примеры.
1) Проведем логарифмирования левой и правой частей
![]()
Найдем производную правой части
![]()
![]()
Производная левой части показана при изложении теоретического материала. Записываем обе части
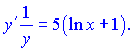
Далее переносим функцию ![]() из знаменателя в правую часть и не забываем поменять ее значение
из знаменателя в правую часть и не забываем поменять ее значение
![]()
Несмотря на сложный вид данный пример полностью решено.
2) Используем свойства логарифма к данному примеру
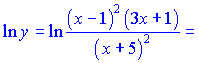
![]()
Проводим дифференцирования обеих частей равенства
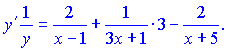
Сведем к общему знаменателю правую сторону. В результате математических операций получим
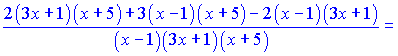
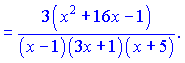
Подставим в исходную равенство, перенеся функцию ![]() в правую часть
в правую часть
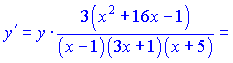
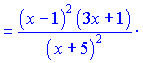
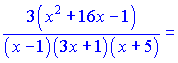
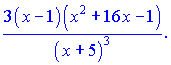
В результате ряда несложных математических манипуляций получили достаточно компактный конечный результат производной. При исчислении данного примера направления подобный результат пришлось бы искать очень долго.
3) Несмотря на сложный вид данное выражение, на основе свойств степеней, можно переписать в следующем виде
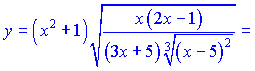
![]()
![]()
Применим к нему логарифмирования
![]()
![]()
Производная от правой части будет равна следующему выражению
![]()
![]()
![]()
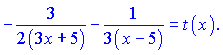
Здесь для упрощения дальнейших выкладок введено обозначение ![]() .
.
Учитывая производную ![]() , окончательно получим
, окончательно получим
![]()
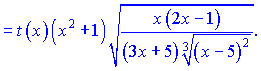
Можно оставлять в таком виде, поскольку суть данного урока научиться применять метод логарифмического дифференцирования. Но если Вы захотите для упрощения свести все к общему знаменателю, то получите следующее выражение
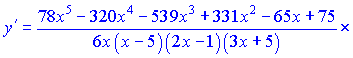
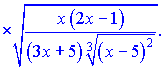
Поверьте это займет у Вас много времени.
4) Проводим логарифмирования функции
![]()
![]()
Дальше по методике находим производную правой части. Она будет равна выражению
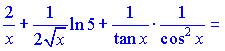
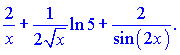
Подставляя в формулу для производной от ![]() , получим
, получим
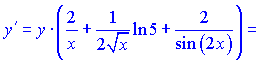
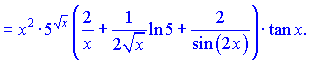
На этом решения примера завершен.
Практикуйте с подобными задачами и через некоторое время у Вас не будет никаких трудностей с такого сорта примерами.


