В геометрии, механике, физике часто встречается параметрический способ задания уравнение, описывающее кривую на плоскости или в пространстве. Саму же линию можно рассматривать как геометрическое место последовательных положений движущейся точки, координаты 
и 
которой являются функциями вспомогательной переменной 
(времени, скорости, расстояния и т.д.) Вспомогательную переменную называют параметром, а уравнение функции – параметрическим. Например, кривая на плоскости определяется двумя уравнениями
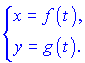
Производная заданной функции первого порядка находится по правилу
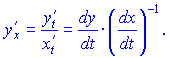
Вторая производная определяется зависимостью
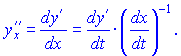
Аналогичным образом можно вывести производные старших рядом.
Рассмотрим несколько примеров для закрепления материала на практике.
Пример 1.
Найти производные функций, заданных параметрически.
(Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")
1) (5.253)
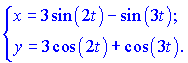
2) (5.256)
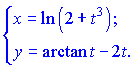
3) (5.261)
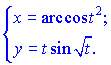
4) (5.263)
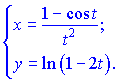
Решение.
1) Вычислим производные функции и аргумента по параметру 
Найденные значения подставляем в формулу
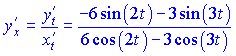
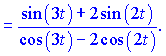
В данном случае, чтобы не выносить знак минус перед дробь, умножим на 
знаменатель и переставим слагаемые так, чтобы первыми шли положительные. Сама же кривая на плоскости будет иметь вид
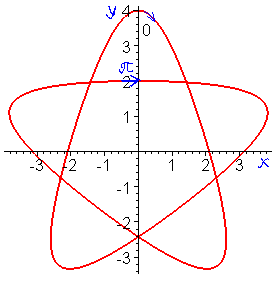
2) Найдем производные по параметру
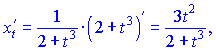
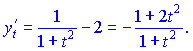
Вычисляем значение производной 
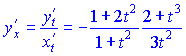
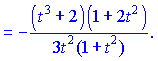
Пример не сложный, главное правильно вычислить производные.
3) Вычисляем производные
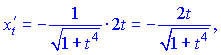
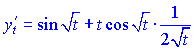
Полученные значения подставим в формулу для производной 
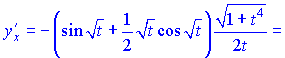
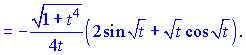
4) Продифференцируем функцию и аргумент по параметру 
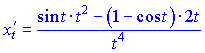
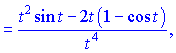
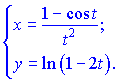
Полученные значения подставляем в формулу и упрощаем числитель и знаменатель на 
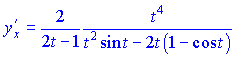
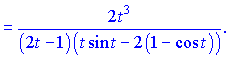
Из примеров видно, что вычисление производной от параметрически заданной функции не слишком сложное. Следуйте последовательности выполнения действий, будьте внимательны при упрощении выражений и все у Вас получится правильно.
