Часто на практике встречаются функции в которых независимая переменная 
и функция 
связаны между собой зависимостью
из которой нельзя отделить саму функцию. В этом случае функция 
называется неявной функцией от
.
Однако саму производную функции по переменной 
можно вычислить. Для этого дифференцируют функцию 
по 
, при этом учитывают, что сама функция зависит от переменной 
. Из полученного уравнения группируют слагаемые, содержащиеся при производной 
и выражают ее.
Для закрепления материала рассмотрим следующие примеры.
Пример 1.
Найти производные функций
, заданных неявно (Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")
1) (5.219)
2) (5.223)
3) (5.227)
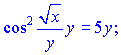
4) (5.236)
Решение.
1) Продифференцируем правую и левую части
Полученное выражение разделим на общий множитель 
и сгруппируем слагаемые, содержащие производную 
и перенесем их в одну сторону за знак равенства. В результате получим
Поделив на множитель при производной 
получим ее значение
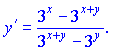
Для упрощения, вынесем из числителя и знаменателя общие множители 
и
соответственно. В результате будем иметь
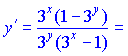
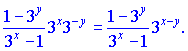
Как видите ничего сложного мы не делали но быстро нашли производную неявно заданной функции. Рассмотрим следующую задачу.
2) Проведем дифференцировки
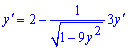
Выделяем слагаемые, содержащие производную
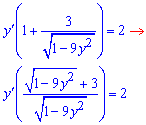
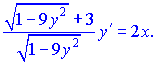
Разделим на множитель при производной и найдем ее значение
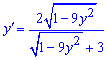
Задача полностью решена.
3) Вычислим производную правой и левой части
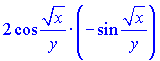
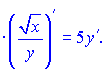
Найдем производную частки функций
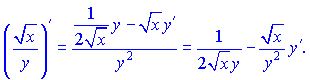
Первых два множителя равны синусу двойного угла. Поэтому производные можем записать в виде
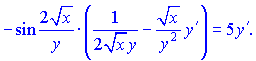
Умножим правую и левую части на
чтобы избавиться знаменателей и сгруппируем слагаемые при производной 
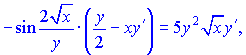
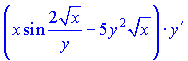
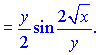
Из последней зависимости находим значение искомой производной
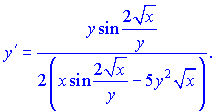
В такого рода примерах главное не ошибиться при отыскании производных.
4) Проведем дифференцирования функций
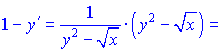
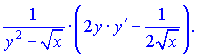
Выделим слагаемые, содержащие 
и сгруппируем их
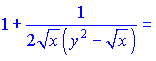
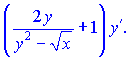
Сведем выражения к общему знаменателю
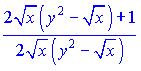
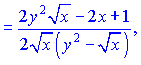
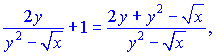
и подставим их на свои места
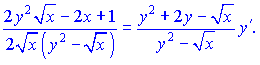
Отсюда выразим производную
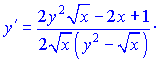
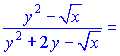
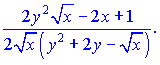
На этом решения примера завершено.
При вычислении производной неявно заданной функции типичными ошибками на практике являются неправильное взятие производной и неразбериха со знаками при группировке подобных слагаемых. Будьте внимательны в таких ситуациях и не допускайте ошибок.
