Научиться вычислять определители, обратные матрицы и т.д. - одно из основных заданий для первокурсников, которые получают образование на факультетах с математическим уклоном в обучении. Многие сервисы в интернете предлагают онлайн нахождения определителей и всего что касается матриц, однако мало программ - математических калькуляторов которые показывают ход решения. В конце статьи Вашему вниманию предлагается такой калькулятор, но об этом позже, а сейчас давайте рассмотрим несколько примеров нахождение определителя матрицы.
За справочник возьмем сборник задач Дубовика В.П., Юрика И.И. "Высшая математика". Позже будут добавлены примеры вычисления определителя матрицы из других источников.
--------------------------------------------
Примеры.
1) (1.4)
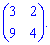
Применим правило вычисления определителя для матрицы второго порядка.
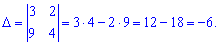
2) (1.6)
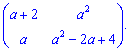
Выполним вычисления согласно правилу
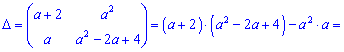
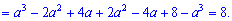
3) (1.8)
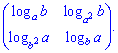
Данный пример выглядит сложным но со знанием следующих правил логарифма
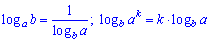
решается на удивление быстро.
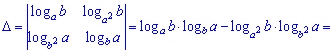
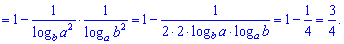
4) (1.14)
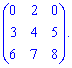
Вычислим данный определитель двумя способами: по правилу треугольников и через алгебраические дополнения.
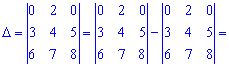
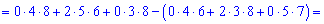
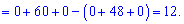
А сейчас разложим по элементам первого рядка, поскольку в нем больше нулей
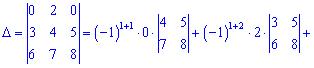
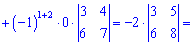
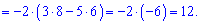
В этом примере специально выписаны дополнение у нулевых множителей, так как не все понимают откуда берутся дополнения. По правилу они равны определителю, который образуется вычеркиванием строки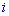 
и столбца 
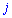того элемента 
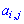для которого ищутся, умноженному на минус единицу в степени
.
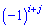Схематически на примере матрицы четвертого порядка это выглядит так:
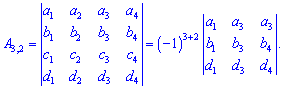
Внимательно посмотрите, какие элементы в определителе выписаны для дополнений и Вам все станет понятно.
Суть метода алгебраических дополнений заключается в том, что когда мы матрицу с нулевыми элементами может разложив ее по по строке или столбцу в котором больше нулей нам остается вычислить столько определителей на порядок меньших основной матрицы, сколько ненулевых элементов. Это значительно упрощает вычисления.
6) (1.19)
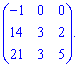
Если вычисления проводить по правилу треугольников, то получим много нулевых произведений. В такого рода примерах целесообразно использовать алгебраические дополнения.
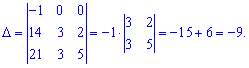
7) (1.21)
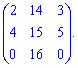
Вычислим определитель через алгебраические дополнения третьей строки
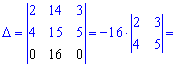
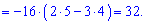
Как можно убедиться, решение с помощью алгебраических дополнений в случаях разреженных матриц можно получить быстро и без большого количества вычислений.
8) (1.58)
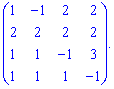
Выполним элементарные преобразования. От другого рядка вычтем первый, а от четвертого - третий. Получим разреженную матрицу
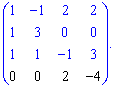
Определитель найдем через алгебраические дополнения к четвертой строке
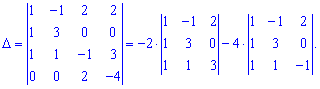
Вычислим каждый из слагаемых
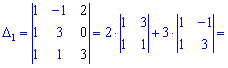
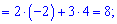
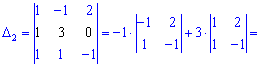
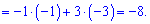
Подставляем в определитель
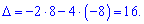
9) (1.72)
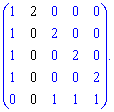
Найдем определитель через расписание по строкам и столбцам, содержащие нули (выделены черным).
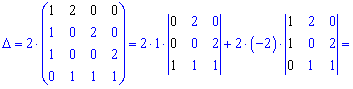
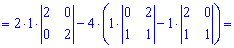
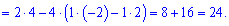
Таким методом нахождения определителя пятого порядка свелось к простым вычислениям. Практикуйте и изучайте правила и через некоторое время у Вас будет выходить не хуже. До встречи в следующих уроках!
----------------------------------------------
