Произведением двух матриц будет матрица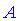 
, элементы которой 
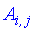равны сумме попарных произведений элементов строки первой матрицы 
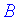на соответствующие элементы столбца второй матрицы 
: 
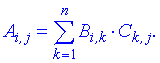
Из этого следует что перемножить между собой можно матрицы в которых количество столбцов первой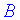 
равно количеству строк второй 
. Новая матрица 
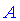которая является произведением двух имеет размерность 
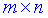, где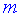 
– количество строк первой матрицы, а 
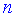– столбцов второй. Правила достаточно просты и для нахождения произведения матриц нужно уметь лиш умножать и прибавлять. Рассмотрим несколько примеров из сборника задач Дубовика В.П., Юрика И.И. "Высшая математика".
--------------------------------------------
Примеры.
Найти произведение матриц.
1) (1.110)
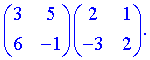
Для нахождения произведения умножаем строки первой матрицы на столбцы второй
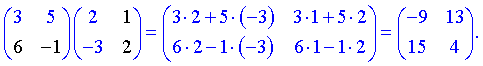
2) (1.112)
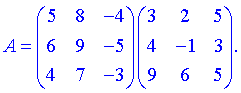
Найдем элементы новой матрицы.
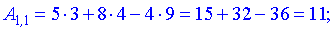
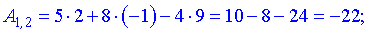
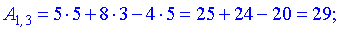
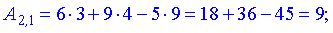
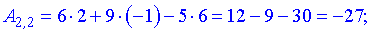
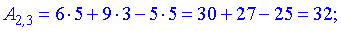
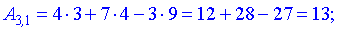
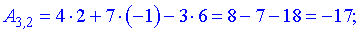
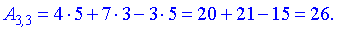
Записываем полученные значения в матрицу.
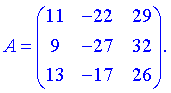
3) (1.114)
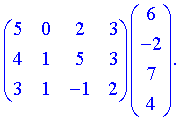
Согласно правилам - произведением будет матрица-вектор размерности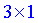 
. Вычислим ее элементы
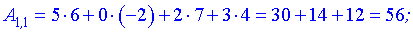
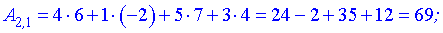
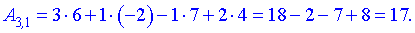
Окончательно матрица примет вид
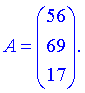
4) (1.115)
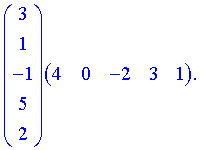
При вычислении произведения матриц-векторов получим квадратную матрицу размера.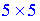 
.
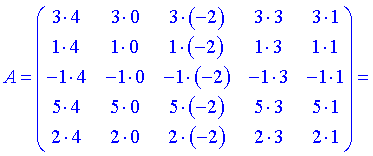
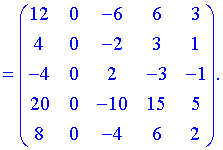
Простыми операциями умножения получили новую квадратную матрицу пятого порядка.
5) (1.116)
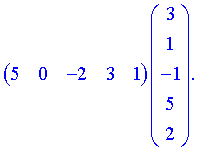
Результатом умножения в данном примере будет матрица которая содержит лиш один элемент.
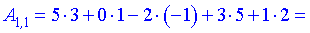
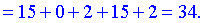
На этом практическая часть урока закончена. Упражняйтесь в решении подобных примеров, ведь умножения - это одна из основных операций (не только в матрицах). В следующих статьях материал будет сложнее, поэтому начинайте знакомиться с матрицами с простого.
